TRIANGLE RECTANGLE - TRIGONOMETRIE
|
I) Triangle rectangle : rappels
A) Définitions
Définition
Un triangle
rectangle est un triangle possédant un angle droit.
Les deux angles qui ne sont pas droits sont complémentaires : leur somme vaut 90°.
Le côté le plus long du triangle rectangle est appelé l'hypoténuse. Il s'agit du côté situé en face de l'angle droit.
Les deux angles qui ne sont pas droits sont complémentaires : leur somme vaut 90°.
Le côté le plus long du triangle rectangle est appelé l'hypoténuse. Il s'agit du côté situé en face de l'angle droit.
Illustration graphique

Remarque
Concernant l'angle \(\widehat{ABC}\) :
- [AB] est le côté
adjacent.
- [AC] est le côté opposé.
Concernant l'angle \(\widehat{ACB}\)
:- [AC] est le côté opposé.
- [AC] est le côté adjacent
- [AB] est le côté opposé.
- [AB] est le côté opposé.
B) Théorème de Pythagore
Théorème
Dans un triangle ABC rectangle en A, la
somme des carrés des longueurs des côtés de l'angle droit est égale au
carré de la longueur de l'hypoténuse :
\[ AB^{2}+AC^{2}=BC^{2} \] Ce théorème est connu sous le nom de "Théorème de Pythagore".
\[ AB^{2}+AC^{2}=BC^{2} \] Ce théorème est connu sous le nom de "Théorème de Pythagore".
Exemple 1 :
Soit le triangle MNK rectangle en N avec MN = 3 cm et NK = 4 cm. Calculer la longueur MK.
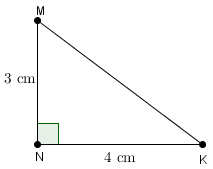
\[ \begin{align*} &MN^{2}+NK^{2}=MK^{2}\\ &MK^{2}=3^{2}+4^{2}\\ &MK^{2}=9+16\\ &MK^{2}=25\\ &MK=\sqrt{25}\\ &MK=5 \text{ cm} \end{align*} \] MK mesure 5 cm.
Exemple 2 :
Le triangle IJK est rectangle en J avec IJ = 6 cm et IK = 10 cm. Calculer la longueur JK.

\[ \begin{align*} &IJ^{2}+JK^{2}=IK^{2}\\ &JK^{2}=IK^{2}-IJ^{2}\\ &JK^{2}=10^{2}-6^{2}\\ &JK^{2}=100-36\\ &JK^{2}=64\\ &JK=\sqrt{64}\\ &JK=8\text{ cm} \end{align*} \] JK mesure 8 cm.
C) Réciproque du théorème de Pythagore
Propriété
Dans un triangle, si le carré de la
longueur du côté le plus long est égal à la somme des carrés des
longueurs des deux autres côtés, alors ce triangle est rectangle.
Exemple 3 :
Soit un triangle ABC tel que AB = 4.5 cm, BC = 6 cm et AC = 7.5 cm. Le triangle ABC est-il rectangle ?
AC est la longueur la plus importante du triangle ABC. On a :
\[ \begin{align*} &AC^{2}=7.5^{2}=56.25\\ &AB^{2}+BC^{2}=4.5^{2}+6^{2}=20.25+36=56.25 \end{align*} \] On remarque que :
\[AB^{2}+BC^{2}=AC^{2}\] donc d'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
Exemple 4 :
Soit un triangle DEF tel que DE = 6 cm, EF = 8 cm et DF = 11 cm. Le triangle DEF est-il rectangle ?
DF est la longueur la plus importante du triangle DEF. On a :
\[\begin{align*} &DF^{2}=11^{2}=121\\ &DE^{2}+EF^{2}=6^{2}+8^{2}=36+64=100\\ \end{align*} \] On remarque que :
\[DE^{2}+EF^{2}\neq \text{D}F^{2}\] donc le triangle DEF n'est pas rectangle.
II) Trigonométrie
Dans toute cette partie, on considère un triangle ABC rectangle en A :
A) Cosinus
Définition
Le cosinus
d'un angle se définit comme le rapport entre la longueur du côté
adjacent à cet angle et la longueur de l'hypoténuse.
\[ \begin{align*} \cos \widehat{ABC}&=\frac{\text{côté adjacent à l'angle }\widehat{ABC}}{\text{hypoténuse}}=\frac{AB}{BC}\\ \cos \widehat{ACB}&=\frac{\text{côté adjacent à l'angle }\widehat{ACB}}{\text{hypoténuse}}=\frac{AC}{BC} \end{align*} \]
\[ \begin{align*} \cos \widehat{ABC}&=\frac{\text{côté adjacent à l'angle }\widehat{ABC}}{\text{hypoténuse}}=\frac{AB}{BC}\\ \cos \widehat{ACB}&=\frac{\text{côté adjacent à l'angle }\widehat{ACB}}{\text{hypoténuse}}=\frac{AC}{BC} \end{align*} \]
Exemple 5 : Calculer la valeur d'un angle.
Soit un triangle ABC rectangle en A tel que AB = 3 cm, AC = 4 cm, et BC = 5 cm. Quel est le cosinus de l'angle\(\widehat{ABC}\) ? Combien mesure l'angle \(\widehat{ABC}\) ?

Pour obtenir la mesure de l'angle \(\widehat{ABC}\), on utilise la touche cos-1 (ou arccos) de la calculatrice :
\[\cos^{-1}(0.6)\approx 53.13^{\circ}\] L'angle \(\widehat{ABC}\) mesure approximativement \(53.13^{\circ}\).
Exemple 6 : Calculer une longueur.
Soit un triangle ABC rectangle en A tel que AC = 10 cm et \(\widehat{ACB}=60^{\circ}\). Combien mesure la longueur BC ?

\[ \begin{align*} \cos \widehat{ACB}&=\frac{\text{côté adjacent à l'angle }\widehat{ACB}}{\text{hypoténuse}}\\ &=\frac{AC}{BC}\\ &=\frac{10}{BC} \end{align*} \] Et d'autre part :
\[\cos \widehat{ACB}=\cos(60)=0.5 \] Par conséquent :
\[\frac{10}{BC}=0.5 \] On en déduit que BC = 20 cm.
B) Sinus
Définition
Le sinus
d'un angle se définit comme le rapport entre la longueur du côté opposé
à cet angle et la longueur de l'hypoténuse.
\[ \begin{align*} \sin \widehat{ABC}&=\frac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{hypoténuse}}=\frac{AC}{BC}\\ \sin \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{hypoténuse}}=\frac{AB}{BC} \end{align*} \]
\[ \begin{align*} \sin \widehat{ABC}&=\frac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{hypoténuse}}=\frac{AC}{BC}\\ \sin \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{hypoténuse}}=\frac{AB}{BC} \end{align*} \]
Exemple 7 : Calculer la valeur d'un angle.
Soit un triangle ABC rectangle en A tel que AB = 3 cm, AC = 4 cm, et BC = 5 cm. Quel est le sinus de l'angle\(\widehat{ABC}\) ? Combien mesure l'angle \(\widehat{ABC}\) ?

Pour obtenir la mesure de l'angle \(\widehat{ABC}\), on utilise la touche sin-1 (ou arcsin) de la calculatrice :
\[\sin^{-1}(0.8)\approx 53.13^{\circ} \] L'angle \(\widehat{ABC}\) mesure approximativement \(53.13^{\circ}\).
Exemple 8 : Calculer une longueur.
Soit un triangle ABC rectangle en A tel que AB = 6 cm et \(\widehat{ACB}=30^{\circ}\). Combien mesure la longueur BC ?

\[\begin{align*} \sin \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{hypoténuse}}\\ &=\frac{AB}{BC}\\ &=\frac{6}{BC} \end{align*} \] Et d'autre part :
\[\sin \widehat{ACB}=\sin(30)=0.5 \] Par conséquent : \[\frac{6}{BC}=0.5 \] On en déduit que BC = 12 cm.
C) Tangente
Définition
La tangente
d'un angle se définit comme le rapport entre la longueur du côté opposé
à cet angle et la longueur du côté adjacent à cet angle.
\[ \begin{align*} \tan \widehat{ABC}&=\frac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{côté adjacent à l'angle }\widehat{ABC}}\\ &=\frac{AC}{AB} \end{align*} \] \[ \begin{align*} \tan \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{côté adjacent à l'angle }\widehat{ACB}}\\ &=\frac{AB}{AC} \end{align*} \]
\[ \begin{align*} \tan \widehat{ABC}&=\frac{\text{côté opposé à l'angle }\widehat{ABC}}{\text{côté adjacent à l'angle }\widehat{ABC}}\\ &=\frac{AC}{AB} \end{align*} \] \[ \begin{align*} \tan \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{côté adjacent à l'angle }\widehat{ACB}}\\ &=\frac{AB}{AC} \end{align*} \]
Exemple 7 : Calculer la valeur d'un angle.
Soit un triangle ABC rectangle en A tel que AB = 3 cm, AC = 4 cm, et BC = 5 cm. Quel est la tangente de l'angle \(\widehat{ABC}\) ? Combien mesure l'angle \(\widehat{ABC}\) ?

Pour obtenir la mesure de l'angle \(\widehat{ABC}\), on utilise la touche tan-1 (ou arctan) de la calculatrice :
\[\tan^{-1}\left(\frac{4}{3}\right)\approx 53.13^{\circ} \] L'angle \(\widehat{ABC}\) mesure approximativement \(53.13^{\circ}\).
Exemple 8 : Calculer une longueur.
Soit un triangle ABC rectangle en A tel que AB = 6 cm et \(\widehat{ACB}=45^{\circ}\). Combien mesure la longueur AC ?

\[ \begin{align*} \tan \widehat{ACB}&=\frac{\text{côté opposé à l'angle }\widehat{ACB}}{\text{côté adjacent à l'angle }\widehat{ACB}}\\ &=\frac{AB}{AC}\\ &=\frac{6}{AC} \end{align*} \] Et d'autre part : \[\tan \widehat{ACB}=\tan(45)=1 \] Par conséquent : \[\frac{6}{AC}=1 \] On en déduit que AC = 6 cm.
C) Remarques diverses
Propriété
Le cosinus, le sinus et la tangente sont
reliés par les relations suivantes :
\[ \begin{align*} &\tan x=\frac{\sin x}{\cos x}\\ &(\cos x)^{2}+(\sin x)^{2}=1 \end{align*} \]
\[ \begin{align*} &\tan x=\frac{\sin x}{\cos x}\\ &(\cos x)^{2}+(\sin x)^{2}=1 \end{align*} \]
Difficile de retenir toutes ces formules ? Il existe un moyen mémo-technique simple :
SOHCAHTOA
pour :
Sinus = Opposé/Hypoténuse ; Cosinus = Adjacent/Hypoténuse ; Tangente = Opposé/Adjacent
Remarquez qu'on ne trouve jamais l'hypoténuse au numérateur !