LOGARITHME NEPERIEN
|
Exercice 1
1) et 3) Représentation graphique :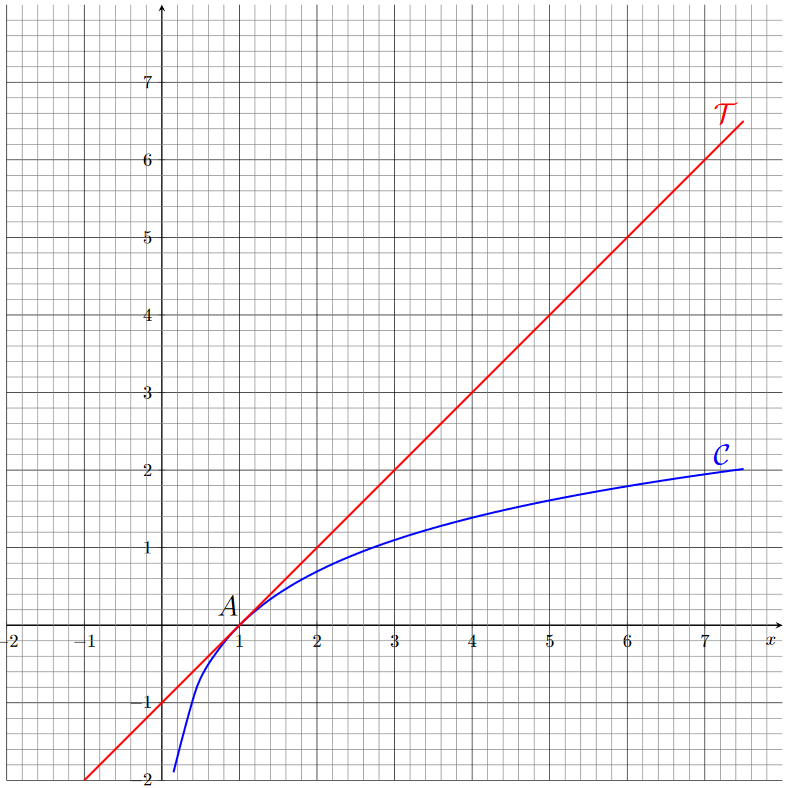
2) L'équation de la tangente à la courbe \(\mathcal C\) au point A(1;0) est : \[ \begin{align*} y(x)&=f(1)+f'(1)(x-1)\\ &=0+1\times (x-1) \\ &=x-1 \end{align*} \]
4) Pour une valeur de \(x\) donnée, \(z\) représente la distance entre la tangente \(T\) et la courbe \(\mathcal{C}\).
On a : \[ \begin{align*} z(x)&=y(x)-f(x) \\ &=x-1-\ln(x) \end{align*} \] Sur le graphique ci-dessous, la flèche représente \(z(4)\).
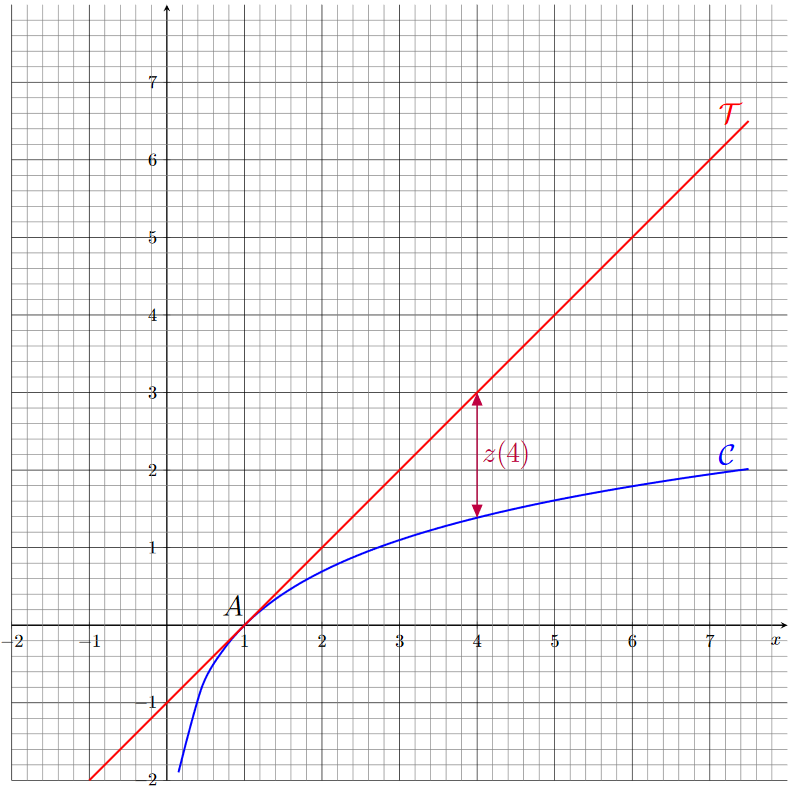
5) Lorsque \(x\) tend vers 1, on s'aperçoit que la distance entre la tangente et la courbe devient de plus en plus petite et tend vers 0.
On le vérifie mathématiquement : \[ \begin{align*} \lim_{x\rightarrow 1} z(x)&=\lim_{x\rightarrow 1} x-1-\ln(x)\\ &=0 \end{align*} \] Lorsque \(x\) tend vers \(0^{+}\), on s'aperçoit que la courbe \(\mathcal{C}\) "plonge" vers \(-\infty\) tandis que la tangente "passe par" -1. La distance tend alors vers \(+\infty\). \[ \begin{align*} \lim_{x\rightarrow 0^{+}} z(x)&=\lim_{x\rightarrow 0^{+}} x-1-\ln(x)\\ &=+\infty \end{align*} \]
6) Calcul de \(\mathcal{A}\) \[ \begin{align*} \mathcal{A}(x)&=\int_{1}^{x}z(t)dt\\ &=\int_{1}^{x}t-1-\ln(t)dt \\ &=\int_{1}^{x}t-1\; dt-\int_{1}^{x}\ln(t)dt \\ &=\left[\frac{t^{2}}{2}-t\right]_{1}^{x}-\int_{1}^{x}\ln(t)dt \\ &=\frac{x^{2}}{2}-x-\left(\frac{1}{2}-1\right)-\int_{1}^{x}\ln(t)dt \\ &=\frac{x^{2}}{2}-x+\frac{1}{2}-\int_{1}^{x}\ln(t)dt \end{align*} \] Cette dernière intégrale se calcule grâce à une intégration par parties. On pose :
\(\displaystyle u=\ln(t) \qquad u'=\frac{1}{t}\)
\(v'=1 \quad \; \, \qquad v=t\)
Alors
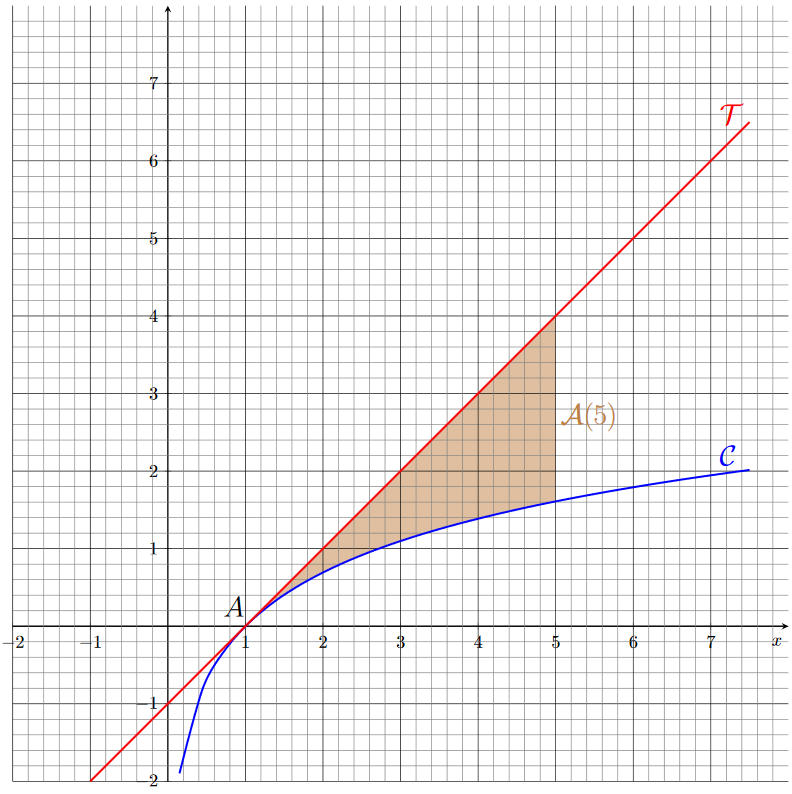
\[ \begin{align*} \int_{1}^{x}\ln(t)dt&=\left[t \ln(t)\right]_{1}^{x}-\int_{1}^{x}\frac{1}{t}t \;dt \\ &=x\ln(x)-1\ln(1)-\int_{1}^{x}1\;dt \\ &=x\ln(x)-\left[t\right]_{1}^{x} \\ &=x\ln(x)-x+1 \end{align*} \] Par conséquent, nous avons : \[ \begin{align*} \mathcal{A}(x)&=\frac{x^{2}}{2}-x+\frac{1}{2}-\left(x\ln(x)-x+1\right)\\ &=\frac{x^{2}}{2}-x+\frac{1}{2}-x\ln(x)+x-1 \\ &=\frac{x^{2}}{2}-x\ln(x)-\frac{1}{2} \end{align*} \] Graphiquement, cette intégrale représente la surface située entre la courbe \(\mathcal{C}\) et la tangente \(\mathcal{T}\), comprise entre 1 et la valeur \(x\) choisie.
Ci dessous, nous-avons représenté \(\mathcal{A}(5)\).
Exercice 2
Partie 11) La fonction \(f\) est définie sur \(\mathbb{R}_{+}^{*}\) et dérivable sur ce même intervalle, et sa dérivée est \[ f'(x)=\frac{1}{x}-1 \] Nous remarquons que \(f'(x)>0\) lorsque \(x<1\), que \(f'(x)=0\) lorsque \(x=1\), et que \(f'(x)<0\) lorsque \(x>1\).
De plus, nous avons : \[ \lim_{x\rightarrow 0^{+}} f(x)=-\infty, \] et \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \] En effet, nous pouvons réécrire \(f\) de la façon suivante : \[ f(x)=x \left[\frac{\ln(x)}{x}-1+\frac{1}{x}\right] \] Comme d'après le cours \[ \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x}=0, \] et \[ \lim_{x\rightarrow +\infty} \frac{1}{x}=0, \] nous avons \[ \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x}-1+\frac{1}{x}=-1, \] et finalement : \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \] De plus, nous avons \[ \begin{align*} f(1)&=\ln(1)-(1-1)\\ &=0. \end{align*} \] Nous pouvons à présent réaliser le tableau de variations de la fonction \(f\) :
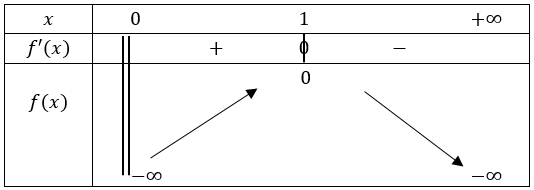
2) D'après le tableau de variations de la fonction \(f\), nous pouvons voir que \(\forall x\in \mathbb{R}^{*}_{+}\), \(f(x)\leq 0\).
Donc \(\forall x\in \mathbb{R}^{*}_{+}\) : \[ \begin{align*} &\ln(x)-(x-1)\leq 0 \\ &\Leftrightarrow \ln(x)\leq(x-1). \end{align*} \]
3) Soit \(g(x)\) la fonction définie sur \(\mathbb{R}_{+}^{*}\) par : \[ g(x)=\ln(x)-\left(1-\frac{1}{x}\right). \] La fonction \(g\) est dérivable sur ce même intervalle, et sa dérivée est \[ \begin{align*} g'(x)&=\frac{1}{x}-\frac{1}{x^{2}} \\ &=\frac{1}{x}\left(1-\frac{1}{x}\right) \end{align*} \] Nous remarquons que \(g'(x)<0\) lorsque \(0 < x < 1\), que \(g'(x)=0\) lorsque \(x=1\), et que \(g'(x)>0\) lorsque \(x>1\).
De plus, nous avons : \[ \lim_{x\rightarrow +\infty} g(x)=+\infty, \] et \[ \lim_{x\rightarrow 0^{+}} g(x)=+\infty. \] En effet, nous pouvons réécrire \(g\) de la façon suivante : \[ g(x)=\frac{1}{x} \left(x\ln(x)-x+1\right) \] Comme d'après le cours \[ \lim_{x\rightarrow 0^{+}} x\ln(x)=0, \] nous avons \[ \lim_{x\rightarrow 0^{+}} x\ln(x)-x+1=1, \] et finalement : \[ \lim_{x\rightarrow 0^{+}} g(x)=+\infty. \] De plus, nous avons \[ \begin{align*} g(1)&=\ln(1)-\left(1-\frac{1}{1}\right)\\ &=0. \end{align*} \] Nous pouvons à présent réaliser le tableau de variations de la fonction \(g\) :
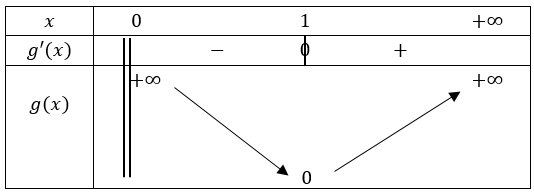
D'après le tableau de variations, nous avons \(g(x)\geq 0, \; \forall x\in \mathbb{R}^{*}_{+}\), ce qui implique finalement : \[ 1-\frac{1}{x}\leq \ln(x) \qquad \forall x\in \mathbb{R}^{*}_{+}. \]
4) A partir de l'inégalité trouvée dans la question 2, en remplaçant \(x\) par \(\displaystyle \frac{p+1}{p}\), on obtient \[ \begin{align*} & \ln \left(\frac{p+1}{p}\right)\leq \frac{p+1}{p}-1 \\ & \Leftrightarrow \ln \left(\frac{p+1}{p}\right)\leq \frac{p+1-p}{p} \\ & \Leftrightarrow \ln \left(\frac{p+1}{p}\right)\leq \frac{1}{p}. \\ \end{align*} \] A partir de l'inégalité trouvée dans la question 3, en remplaçant \(x\) par \(\displaystyle \frac{p+1}{p}\), on obtient \[ \begin{align*} & 1-\frac{1}{\frac{p+1}{p}}\leq \ln \left(\frac{p+1}{p}\right)\\ & 1-\frac{p}{p+1}\leq \ln \left(\frac{p+1}{p}\right)\\ & \frac{(p+1)-p}{p+1}\leq \ln \left(\frac{p+1}{p}\right)\\ & \frac{1}{p+1}\leq \ln \left(\frac{p+1}{p}\right)\\ \end{align*} \] En combinant ces deux inégalités, nous obtenons finalement : \[ \frac{1}{p+1}\leq \ln \left(\frac{p+1}{p}\right)\leq \frac{1}{p}, \qquad \forall p\in \mathbb{N}^{*}. \]
Partie 2
On considère une suite \(u_{n}\) définie par \[ u_{n}=\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{2n}, \; \forall n\in \mathbb{N}^{*} \] 5) Calcul de \(u_{1}\) :
\(\displaystyle u_{1}=\frac{1}{1}+\frac{1}{2}=\frac{3}{2}\)
Calcul de \(u_{2}\) :
\(\displaystyle u_{2}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}\)
Calcul de \(u_{3}\) :
\(\displaystyle u_{3}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}=\frac{147}{60}\)
6) A partir de l'encadrement réalisé à la question 4, nous avons : \[ \begin{align*} &\frac{1}{n+1}\leq \ln \left(\frac{n+1}{n}\right) \leq \frac{1}{n} \\ &\frac{1}{n+2}\leq \ln \left(\frac{n+2}{n+1}\right) \leq \frac{1}{n+1} \\ &\frac{1}{n+3}\leq \ln \left(\frac{n+3}{n+2}\right) \leq \frac{1}{n+2} \\ & \ldots \\ &\frac{1}{2n}\leq \ln \left(\frac{2n}{2n-1}\right) \leq \frac{1}{2n-1} \end{align*} \] En sommant tous les membres de gauche de ces inégalités, nous avons : \[ \frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n+3}+\ldots+\frac{1}{2n}. \] En sommant tous les membres centraux de ces inégalités, nous avons : \[ \begin{align*} &\ln \left(\frac{n+1}{n}\right)+\ln \left(\frac{n+2}{n+1}\right)+\ln \left(\frac{n+3}{n+2}\right)+\ldots + \ln \left(\frac{2n}{2n-1}\right) \\ &=\ln(n+1)-\ln(n)+\ln(n+2)-\ln(n+1)\\ &\qquad +\ln(n+3)-\ln(n+2)+\ldots +\ln(2n)-\ln(2n-1). \\ &=-\ln(n)+\ln(2n)\\ &=-\ln(n)+\ln(2)+\ln(n)\\ &=\ln(2) \end{align*} \] En sommant tous les membres de droite de ces inégalités, nous avons : \[ \begin{align*} &\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{2n-1} \\ &=\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+\ldots+\frac{1}{2n-1}+\frac{1}{2n}-\frac{1}{2n}\\ &=\frac{1}{n}+u_{n}-\frac{1}{2n}\\ &=u_{n}+\frac{1}{2n}\\ \end{align*} \] Finalement, nous obtenons : \[ u_{n}\leq \ln(2) \leq u_{n}+\frac{1}{n}. \]
7) Nous avons \[ \lim_{n \rightarrow +\infty}\frac{1}{n}=0 \] Par suite, nous avons \[ \lim_{n \rightarrow +\infty}u_{n}=\ln(2), \] donc la suite \(u_{n}\) converge vers \(\ln(2)\).