LOGARITHME NEPERIEN
|
Dans le chapitre précédent, nous avons étudié la fonction exponentielle. Nous savons résoudre l'équation \(e^{x}=1\), la solution étant \(x=0\), ou encore les équations du type \(e^{x}=e^{a}\), la solution étant \(x=a\). Par contre nous ne savons pas encore résoudre les équations du type \(e^{x}=a\), avec \(a\) un réel strictement positif.
Nous allons étudier pour cela une nouvelle fonction, la fonction logarithme népérien, qui permet de résoudre ces équations.
I) Définition
Reprenons ce que nous avons vu sur la fonction exponentielle. La fonction exponentielle est continue et strictement croissante sur \(-]\infty;+\infty[\). Elle est telle que \[ \lim_{x\rightarrow -\infty} e^{x}=0, \] et \[ \lim_{x\rightarrow +\infty} e^{x}=+\infty. \] Elle réalise par conséquent une bijection de \(]-\infty;+\infty[\) vers \(]0;+\infty[\).En utilisant le théorème des valeurs intermédiaires, nous pouvons prouver que pour tout réel strictement positif \(a\), l'équation \(e^{x}=a\) admet une unique solution dans \(\mathbb{R}\).
Cette solution est le logarithme népérien du nombre réel strictement positif \(a\), que l'on note \(\ln(a)\).
Définition 1
Pour tout réel strictement positif \(a\), le logarithme népérien de \(a\) est l'unique réel dont l'exponentielle est égale à \(\ln(a)\), et on le note \(\ln(a)\).
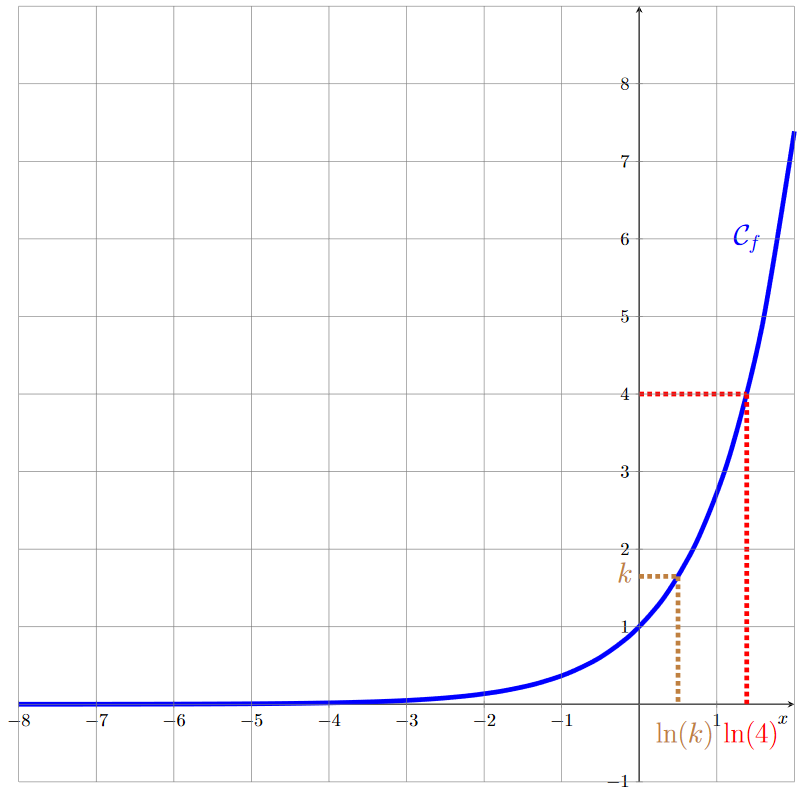
Sur le graphique suivant, l'équation \(e^{x}=4\) admet une solution unique : \(x=\ln(4)\approx 1.39\). Ainsi pour tout réel strictement positif \(k\), nous pouvons résoudre l'équation \(e^{x}=k\), et la solution est \(x=\ln(k)\).
Compte-tenu de la définition du logarithme népérien, nous avons la propriété suivante.
Propriété 1
Pour tout réel \(a\) et tout réel strictement positif \(b\) :
\[
e^{a}=b \Leftrightarrow a=\ln(b).
\]
Il découle de la Propriété 1 la propriété suivante.
Propriété 2
Pour tout réel strictement positif \(a\) :
\[
e^{\ln(a)}=a.
\]
Pour tout réel \(a\) :
\[
\ln\left(e^{a}\right)=a
\]
Les propriétés 1 et 2 permettent de donner certaines valeurs remarquables du logarithme népérien. La première concerne \(\ln(1)\). \[ \begin{align*} \ln(1)&=\ln \left(e^{0}\right) \\ &=0 \text{ (d'après la Propriété 2)} \end{align*} \] La seconde concerne \(\ln(e)\). \[ \begin{align*} \ln(e)&=\ln \left(e^{1}\right) \\ &=1 \text{ (d'après la Propriété 2)} \end{align*} \]
II) Propriétés algébriques
Propriété 3
Pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\) :
\[
\ln(a\times b)=\ln(a)+\ln(b)
\]
Démonstration :
Pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\), nous avons d'une part : \[ e^{\ln(a\times b)}=a\times b, \] et d'autre part, \[ e^{\ln(a)+\ln(b)}=e^{\ln(a)}\times e^{\ln(b)}=a\times b. \] Nous avons par conséquent : \[ e^{\ln(a\times b)}=e^{\ln(a)+\ln(b)}=a\times b. \] Etant donné que deux réels \(\ln(a\times b)\) et \(\ln(a)+\ln(b)\) ont exactement la même exponentielle, nous pouvons en conclure qu'ils sont égaux. On a bien démontré que : \[ \ln(a\times b)=\ln(a)+\ln(b). \]
Pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\), nous avons d'une part : \[ e^{\ln(a\times b)}=a\times b, \] et d'autre part, \[ e^{\ln(a)+\ln(b)}=e^{\ln(a)}\times e^{\ln(b)}=a\times b. \] Nous avons par conséquent : \[ e^{\ln(a\times b)}=e^{\ln(a)+\ln(b)}=a\times b. \] Etant donné que deux réels \(\ln(a\times b)\) et \(\ln(a)+\ln(b)\) ont exactement la même exponentielle, nous pouvons en conclure qu'ils sont égaux. On a bien démontré que : \[ \ln(a\times b)=\ln(a)+\ln(b). \]
Propriété 4
Pour tout \(a\in \mathbb{R}^{*}_{+}\) :
\[
\ln \left(\frac{1}{a}\right)=-\ln(a)
\]
Démonstration :
Nous pouvons démontrer cette propriété en utilisant l'égalité \(\ln(1)=0\) ainsi que la propriété 3. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} \ln(a)+\ln \left(\frac{1}{a}\right)&=\ln \left(a\times \frac{1}{a}\right)\\ &=\ln(1)\\ &=0. \end{align*} \] Par conséquent, nous avons : \[ \ln \left(\frac{1}{a}\right)=-\ln(a), \] soit la propriété 4.
Nous pouvons démontrer cette propriété en utilisant l'égalité \(\ln(1)=0\) ainsi que la propriété 3. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} \ln(a)+\ln \left(\frac{1}{a}\right)&=\ln \left(a\times \frac{1}{a}\right)\\ &=\ln(1)\\ &=0. \end{align*} \] Par conséquent, nous avons : \[ \ln \left(\frac{1}{a}\right)=-\ln(a), \] soit la propriété 4.
Propriété 5
Pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\) :
\[
\ln \left(\frac{a}{b}\right)=\ln(a)-\ln(b)
\]
Démonstration :
Nous pouvons démontrer cette propriété en utilisant les propriétés 3 et 4. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} \ln \left(\frac{a}{b}\right)&=\ln \left(a \times \frac{1}{b}\right)\\ &=\ln(a)+\ln \left(\frac{1}{b}\right) \text{ (d'après la Propriété 3)}\\ &=\ln(a)+(-\ln(b)) \text{ (d'après la Propriété 4)} \\ &=\ln(a)-\ln(b). \end{align*} \] Nous avons bien \(\displaystyle \ln \left(\frac{a}{b}\right)=\ln(a)-\ln(b)\), soit la propriété 5.
Nous pouvons démontrer cette propriété en utilisant les propriétés 3 et 4. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(b\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} \ln \left(\frac{a}{b}\right)&=\ln \left(a \times \frac{1}{b}\right)\\ &=\ln(a)+\ln \left(\frac{1}{b}\right) \text{ (d'après la Propriété 3)}\\ &=\ln(a)+(-\ln(b)) \text{ (d'après la Propriété 4)} \\ &=\ln(a)-\ln(b). \end{align*} \] Nous avons bien \(\displaystyle \ln \left(\frac{a}{b}\right)=\ln(a)-\ln(b)\), soit la propriété 5.
Propriété 6
Pour tout \(a\in \mathbb{R}^{*}_{+}\) et tout \(n\in \mathbb{Z}\) :
\[
\ln (a^{n})=n\ln(a)
\]
Démonstration :
Nous allons démontrer cette propriété par récurrence et à l'aide de la Propriété 3. Nous considérons d'abord le cas \(n\in \mathbb{N}\).
Initialisation : \(n=0\)
Pour tout \(a\in \mathbb{R}^{*}_{+}\), \[ \ln(a^{0})=\ln(1)=0=0\ln(a) \] donc la propriété est vraie au rang 0.
Hérédité : Supposons la propriété vraie au rang \(n\). Alors pour tout \(a\in \mathbb{R}^{*}_{+}\) : \[ \begin{align*} \ln (a^{n+1})&=\ln(a^{n}\times a) \\ &=\ln(a^{n})+\ln(a) \text{ (d'après la Propriété 3)}\\ &=n\ln(a)+\ln(a) \text{ (par hypothèse de récurrence)}\\ &=(n+1)\ln(a) \end{align*} \] donc la propriété est vraie au rang \(n+1\).
Conclusion : \(\forall a\in \mathbb{R}^{*}_{+}\), \(\forall n\in \mathbb{N}\), nous avons \(\ln (a^{n})=n\ln(a)\).
Dans le cas où \(n\) est un entier relatif négatif, nous allons utiliser la Propriété 4 pour démontrer le résultat voulu. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) : \[ \begin{align*} \ln(a^{n})&=\ln \left(\frac{1}{a^{-n}}\right) \\ &=-\ln(a^{-n}) \text{ (d'après la Propriété 4)}\\ &=-(-n\ln(a)) \\ &=n\ln(a) \end{align*} \] car \(-n\) est positif et d'après la récurrence précédente. La propriété est également vraie pour les entiers relatifs négatifs.
Nous avons bien \(\forall a\in \mathbb{R}^{*}_{+}\), \(\forall n\in \mathbb{Z}\), \(\ln (a^{n})=n\ln(a)\), soit la Propriété 6.
Nous allons démontrer cette propriété par récurrence et à l'aide de la Propriété 3. Nous considérons d'abord le cas \(n\in \mathbb{N}\).
Initialisation : \(n=0\)
Pour tout \(a\in \mathbb{R}^{*}_{+}\), \[ \ln(a^{0})=\ln(1)=0=0\ln(a) \] donc la propriété est vraie au rang 0.
Hérédité : Supposons la propriété vraie au rang \(n\). Alors pour tout \(a\in \mathbb{R}^{*}_{+}\) : \[ \begin{align*} \ln (a^{n+1})&=\ln(a^{n}\times a) \\ &=\ln(a^{n})+\ln(a) \text{ (d'après la Propriété 3)}\\ &=n\ln(a)+\ln(a) \text{ (par hypothèse de récurrence)}\\ &=(n+1)\ln(a) \end{align*} \] donc la propriété est vraie au rang \(n+1\).
Conclusion : \(\forall a\in \mathbb{R}^{*}_{+}\), \(\forall n\in \mathbb{N}\), nous avons \(\ln (a^{n})=n\ln(a)\).
Dans le cas où \(n\) est un entier relatif négatif, nous allons utiliser la Propriété 4 pour démontrer le résultat voulu. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) : \[ \begin{align*} \ln(a^{n})&=\ln \left(\frac{1}{a^{-n}}\right) \\ &=-\ln(a^{-n}) \text{ (d'après la Propriété 4)}\\ &=-(-n\ln(a)) \\ &=n\ln(a) \end{align*} \] car \(-n\) est positif et d'après la récurrence précédente. La propriété est également vraie pour les entiers relatifs négatifs.
Nous avons bien \(\forall a\in \mathbb{R}^{*}_{+}\), \(\forall n\in \mathbb{Z}\), \(\ln (a^{n})=n\ln(a)\), soit la Propriété 6.
Propriété 7
Pour tout \(a\in \mathbb{R}^{*}_{+}\) :
\[
\ln \left(\sqrt{a}\right)=\frac{1}{2}\ln(a)
\]
Démonstration :
Nous allons démontrer cette propriété à l'aide de la Propriété 6. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} 2\ln(\sqrt{a})&=\ln \left((\sqrt{a})^{2}\right) \text{ (d'après la Propriété 6)}\\ &=\ln(a) \end{align*} \] donc en déduit que : \[ \ln \left(\sqrt{a}\right)=\frac{1}{2}\ln(a), \] soit la Propriété 7.
Nous allons démontrer cette propriété à l'aide de la Propriété 6. En effet, pour tout \(a\in \mathbb{R}^{*}_{+}\) nous avons : \[ \begin{align*} 2\ln(\sqrt{a})&=\ln \left((\sqrt{a})^{2}\right) \text{ (d'après la Propriété 6)}\\ &=\ln(a) \end{align*} \] donc en déduit que : \[ \ln \left(\sqrt{a}\right)=\frac{1}{2}\ln(a), \] soit la Propriété 7.
III) Propriétés analytiques
Après avoir défini le logarithme népérien d'un réel strictement positif, nous allons définir la fonction logarithme népérien et étudier ses propriétés.Définition 2
On appelle fonction logarithme népérien la fonction qui, à tout réel strictement positif \(x\), associe \(\ln(x)\).
\[
\begin{align*}
\ln : \mathbb{R}^{*}_{+}&\longrightarrow \mathbb{R} \\
x&\longrightarrow \ln(x)
\end{align*}
\]
Nous commençons par étudier la dérivabilité de la fonction logarithme népérien.
Théorème 1
La fonction \(x\longrightarrow \ln(x)\) est dérivable sur \(\mathbb{R}^{*}_{+}\), et pour tout \(x\in \mathbb{R}^{*}_{+}\) :
\[
\left(\ln(x)\right)'=\frac{1}{x}.
\]
Démonstration : Soit \(x\in \mathbb{R}^{*}_{+}\). Nous allons devoir démontrer que :
\[
\lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}=\frac{1}{x}
\]
Démontrons dans un premier temps que c'est vrai lorsque \(x=1\) (en fait, on aura besoin de ce résultat dans la suite de la démonstration).
On souhaite démontrer que : \[ \lim_{h\rightarrow 0}\frac{\ln(1+h)-\ln(1)}{h}=1 \qquad (*) \] Pour cela, nous allons poser \(H=\ln(1+h)\). Ceci nous donne \(h=e^{H}-1\), et par suite : \[ \begin{align*} \frac{\ln(1+h)-\ln(1)}{h}&=\frac{H-0}{e^{H}-1}\\ &=\frac{H}{e^{H}-1} \\ &=\frac{1}{\frac{e^{H}-1}{H}} \end{align*} \] Or dans le chapitre sur les exponentielles, nous avons vu que \[ \lim_{H\rightarrow 0}\frac{e^{H}-1}{H}=1, \] car il s'agit du nombre dérivé de la fonction exponentielle en 0. Par suite, nous avons \[ \lim_{h\rightarrow 0}\frac{\ln(1+h)-\ln(1)}{h}=1 \] Maintenant, revenons à la limite que l'on souhaite démontrer : \[ \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}=\frac{1}{x} \] Partons de l'expression suivante : \[ \begin{align*} \frac{\ln(x+h)-\ln(x)}{h}&=\frac{\ln\left(\frac{x+h}{x}\right)}{h}\text{ (d'après la Propriété 5)} \\ &=\frac{\ln\left(1+\frac{h}{x}\right)}{h} \end{align*} \] On divise à présent le numérateur et le dénominateur par \(x\) (qui est strictement positif) : \[ \begin{align*} \frac{\ln(x+h)-\ln(x)}{h}&=\frac{1}{x}\frac{\ln\left(1+\frac{h}{x}\right)}{\frac{h}{x}} \end{align*} \] Or : \[ \begin{align*} \lim_{h\rightarrow 0} \frac{\ln\left(1+\frac{h}{x}\right)}{\frac{h}{x}}&=\lim_{H\rightarrow 0} \frac{\ln(1+H)}{H} \\ &=\lim_{H\rightarrow 0} \frac{\ln(1+H)-\ln(1)}{H}\\ &=1 \text{ en utilisant la relation } (*) \end{align*} \] On obtient ainsi le résultat désiré : \[ \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}=\frac{1}{x}. \]
Remarque : Une autre possibilité consiste à utiliser la Propriété 2 ainsi que la propriété de dérivation des fonctions composées. En effet, comme \(e^{\ln(x)}=x\), nous avons : \[ \begin{align*} &\left(e^{\ln(x)}\right)'=x'\\ \Longleftrightarrow & \left(\ln(x)\right)'\times e^{\ln(x)}=1\\ \Longleftrightarrow & \left(\ln(x)\right)'\times x=1 \\ \Longleftrightarrow & \left(\ln(x)\right)'=\frac{1}{x} \end{align*} \]
On souhaite démontrer que : \[ \lim_{h\rightarrow 0}\frac{\ln(1+h)-\ln(1)}{h}=1 \qquad (*) \] Pour cela, nous allons poser \(H=\ln(1+h)\). Ceci nous donne \(h=e^{H}-1\), et par suite : \[ \begin{align*} \frac{\ln(1+h)-\ln(1)}{h}&=\frac{H-0}{e^{H}-1}\\ &=\frac{H}{e^{H}-1} \\ &=\frac{1}{\frac{e^{H}-1}{H}} \end{align*} \] Or dans le chapitre sur les exponentielles, nous avons vu que \[ \lim_{H\rightarrow 0}\frac{e^{H}-1}{H}=1, \] car il s'agit du nombre dérivé de la fonction exponentielle en 0. Par suite, nous avons \[ \lim_{h\rightarrow 0}\frac{\ln(1+h)-\ln(1)}{h}=1 \] Maintenant, revenons à la limite que l'on souhaite démontrer : \[ \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}=\frac{1}{x} \] Partons de l'expression suivante : \[ \begin{align*} \frac{\ln(x+h)-\ln(x)}{h}&=\frac{\ln\left(\frac{x+h}{x}\right)}{h}\text{ (d'après la Propriété 5)} \\ &=\frac{\ln\left(1+\frac{h}{x}\right)}{h} \end{align*} \] On divise à présent le numérateur et le dénominateur par \(x\) (qui est strictement positif) : \[ \begin{align*} \frac{\ln(x+h)-\ln(x)}{h}&=\frac{1}{x}\frac{\ln\left(1+\frac{h}{x}\right)}{\frac{h}{x}} \end{align*} \] Or : \[ \begin{align*} \lim_{h\rightarrow 0} \frac{\ln\left(1+\frac{h}{x}\right)}{\frac{h}{x}}&=\lim_{H\rightarrow 0} \frac{\ln(1+H)}{H} \\ &=\lim_{H\rightarrow 0} \frac{\ln(1+H)-\ln(1)}{H}\\ &=1 \text{ en utilisant la relation } (*) \end{align*} \] On obtient ainsi le résultat désiré : \[ \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}=\frac{1}{x}. \]
Remarque : Une autre possibilité consiste à utiliser la Propriété 2 ainsi que la propriété de dérivation des fonctions composées. En effet, comme \(e^{\ln(x)}=x\), nous avons : \[ \begin{align*} &\left(e^{\ln(x)}\right)'=x'\\ \Longleftrightarrow & \left(\ln(x)\right)'\times e^{\ln(x)}=1\\ \Longleftrightarrow & \left(\ln(x)\right)'\times x=1 \\ \Longleftrightarrow & \left(\ln(x)\right)'=\frac{1}{x} \end{align*} \]
Propriété 8
La fonction logarithme népérien est strictement croissante sur \(\mathbb{R}^{*}_{+}\).
Démonstration 1
A partir du Théorème 1, nous avons \(f'(x)>0\), donc la fonction logarithme népérien est strictement croissante sur \(\mathbb{R}^{*}_{+}\).
Démonstration 2 (par l'absurde)
Imaginons que pour deux réels strictement positifs, tels que \(a < b\), nous ayons \[ \ln(a)>\ln(b). \] Alors par croissance de la fonction exponentielle : \[ e^{\ln(a)}>e^{\ln(b)}, \] puis en utilisant la Propriété 2 : \[ a>b, \] ce qui contredit l'hypothèse de départ.
On a donc \(\ln(a)<\ln(b)\) lorsque \(a < b\), donc la fonction \(\ln\) est strictement croissante sur \(\mathbb{R}^{*}_{+}\).
A partir du Théorème 1, nous avons \(f'(x)>0\), donc la fonction logarithme népérien est strictement croissante sur \(\mathbb{R}^{*}_{+}\).
Démonstration 2 (par l'absurde)
Imaginons que pour deux réels strictement positifs, tels que \(a < b\), nous ayons \[ \ln(a)>\ln(b). \] Alors par croissance de la fonction exponentielle : \[ e^{\ln(a)}>e^{\ln(b)}, \] puis en utilisant la Propriété 2 : \[ a>b, \] ce qui contredit l'hypothèse de départ.
On a donc \(\ln(a)<\ln(b)\) lorsque \(a < b\), donc la fonction \(\ln\) est strictement croissante sur \(\mathbb{R}^{*}_{+}\).
Intéressons-nous à présent aux limites aux bornes de l'intervalle de définition de la fonction \(\ln\).
Propriété 9
\[
\begin{align*}
&\lim_{x\rightarrow +\infty}\ln(x)=+\infty
&\text{ et } \qquad
&\lim_{x\rightarrow 0^{+}}\ln(x)=-\infty
\end{align*}
\]
Démonstration
On utilise la définition d'une limite infinie à l'infini.
Dire que la fonction \(\ln\) tend vers \(+\infty\) signifie que quel que soit \(m\in \mathbb{R}\) que l'on se fixe, alors il existe \(x_{0}\) tel que pour tout \(x > x_{0}\), on a \(f(x) > m\).
Ici, en prenant \(x_{0}=e^{m}\), nous pouvons démontrer que \(\ln\) tend vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\).
En effet, quel que soit le réel \(m\) que l'on se fixe, il existe \(x_{0}=e^{m}\) tel que pour tout \(x > x_{0}\), \(\ln(x) > m\), donc \(\ln\) tend vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\).
D'autre part, nous avons \[ \begin{align*} \lim_{x\rightarrow 0^{+}}\ln(x)&=\lim_{X\rightarrow +\infty}\ln \left(\frac{1}{X}\right)\\ &=\lim_{X\rightarrow +\infty}-\ln(X) \text{ (d'après la Propriété 4)}\\ &=-\infty \end{align*} \]
On utilise la définition d'une limite infinie à l'infini.
Dire que la fonction \(\ln\) tend vers \(+\infty\) signifie que quel que soit \(m\in \mathbb{R}\) que l'on se fixe, alors il existe \(x_{0}\) tel que pour tout \(x > x_{0}\), on a \(f(x) > m\).
Ici, en prenant \(x_{0}=e^{m}\), nous pouvons démontrer que \(\ln\) tend vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\).
En effet, quel que soit le réel \(m\) que l'on se fixe, il existe \(x_{0}=e^{m}\) tel que pour tout \(x > x_{0}\), \(\ln(x) > m\), donc \(\ln\) tend vers \(+\infty\) lorsque \(x\) tend vers \(+\infty\).
D'autre part, nous avons \[ \begin{align*} \lim_{x\rightarrow 0^{+}}\ln(x)&=\lim_{X\rightarrow +\infty}\ln \left(\frac{1}{X}\right)\\ &=\lim_{X\rightarrow +\infty}-\ln(X) \text{ (d'après la Propriété 4)}\\ &=-\infty \end{align*} \]
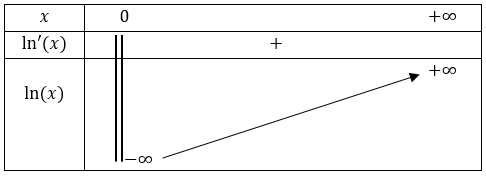
Nous pouvons à présent établir le tableau de variations de la fonction \(\ln(x)\).
Ci-dessous nous représentons graphiquement la fonction \(\ln(x)\) en rouge.
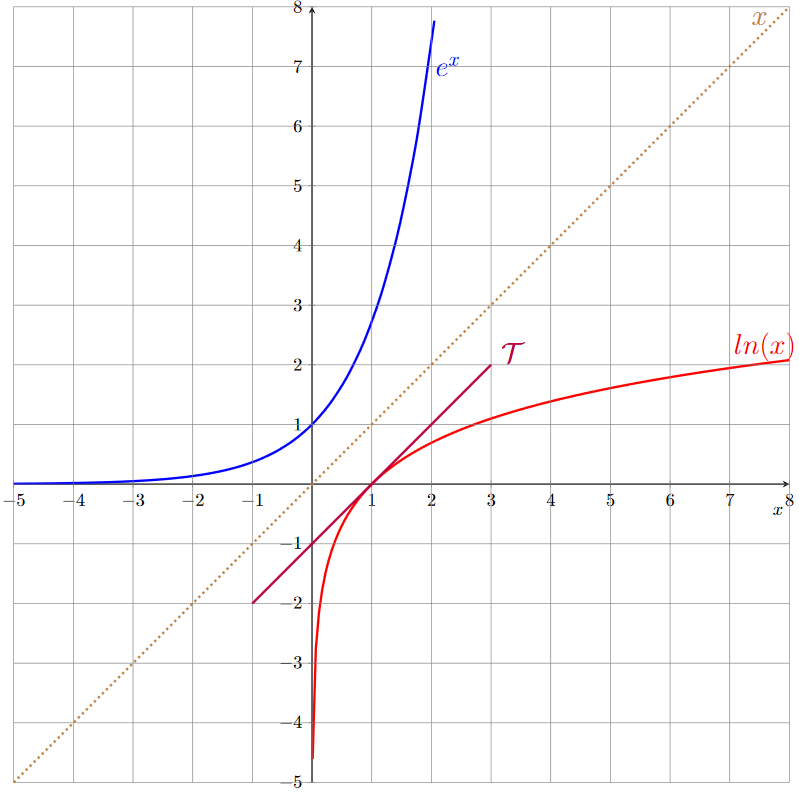
Nous avons vu précédemment que \(\lim_{x\rightarrow 0^{+}} \ln(x)=-\infty\), donc l'axe des ordonnées est asymptote à la courbe représentative de la fonction \(\ln\).
Nous observons bien la croissance de la fonction \(\ln\), mais nous pouvons voir que \(\ln\) tend vers \(+\infty\) beaucoup moins rapidement que \(x\). Cela traduit graphiquement le Théorème 2 que nous verrons par la suite dans ce cours.
Nous montrerons dans l'exercice 1 des exercices d'approfondissement que l'équation de la tangente à la courbe représentative de \(\ln\) au point \((1;0)\) est \(y=x-1\). On a représenté sur le graphique la courbe représentative de cette tangente, notée \(\mathcal{T}\).
Enfin, nous pouvons observer que les courbes représentatives des fonctions logarithme népérien et exponentielle sont symétriques par rapport à la droite d'équation \(y=x\). Cela provient du fait que ces deux fonctions sont réciproques l'une de l'autre.
Certains calculs de limites avec le logarithme népérien peuvent poser (momentanément) problème.
Si on souhaite calculer \(\lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}\), on se trouve en face d'une forme indéterminée, du type \(\frac{+\infty}{+\infty}\).
C'est aussi le cas lorsqu'on souhaite calculer \(\lim_{x\rightarrow 0^{+}}x\ln(x)\) où on a une forme indéterminée du type \(0\times (-\infty)\). Le théorème suivant lève l'indétermination de ces deux limites.
Théorème 2
\[
\begin{align*}
&\lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}=0
&\text{ et } \qquad
&\lim_{x\rightarrow 0^{+}}x\ln(x)=0
\end{align*}
\]
Démonstration
Posons \(X=\ln(x)\). Alors : \[ \begin{align*} \lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}&=\lim_{X\rightarrow +\infty}\frac{X}{e^{X}}\\ &=\lim_{X\rightarrow +\infty}\frac{1}{\frac{e^{X}}{X}} \end{align*} \] Or nous avons vu dans le cours sur les exponentielles que \(\lim_{X\rightarrow +\infty}\frac{e^{X}}{X}=+\infty\). Par conséquent \[ \lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}=0 \] soit la première limite énoncée dans le Théorème 2.
Posons \(X=\frac{1}{x}\). Alors : \[ \begin{align*} \lim_{x\rightarrow 0^{+}}x\ln(x)&=\lim_{X\rightarrow +\infty}\frac{1}{X}\ln \left(\frac{1}{X}\right)\\ &=\lim_{X\rightarrow +\infty}-\frac{\ln(X)}{X} \text{ (d'après la Propriété 4)}\\ &=0 \end{align*} \]
Posons \(X=\ln(x)\). Alors : \[ \begin{align*} \lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}&=\lim_{X\rightarrow +\infty}\frac{X}{e^{X}}\\ &=\lim_{X\rightarrow +\infty}\frac{1}{\frac{e^{X}}{X}} \end{align*} \] Or nous avons vu dans le cours sur les exponentielles que \(\lim_{X\rightarrow +\infty}\frac{e^{X}}{X}=+\infty\). Par conséquent \[ \lim_{x\rightarrow +\infty}\frac{\ln(x)}{x}=0 \] soit la première limite énoncée dans le Théorème 2.
Posons \(X=\frac{1}{x}\). Alors : \[ \begin{align*} \lim_{x\rightarrow 0^{+}}x\ln(x)&=\lim_{X\rightarrow +\infty}\frac{1}{X}\ln \left(\frac{1}{X}\right)\\ &=\lim_{X\rightarrow +\infty}-\frac{\ln(X)}{X} \text{ (d'après la Propriété 4)}\\ &=0 \end{align*} \]
Dans cette section, il nous reste à voir un dernier résultat sur la dérivée de la fonction \(x\rightarrow \ln \left(u(x)\right)\).
Théorème 3
Soit \(u\) une fonction dérivable sur un intervalle \(I\) et strictement positive. Soit \(f\) la fonction définie par
\[
\begin{align*}
f:I&\longrightarrow \mathbb{R} \\
x&\longrightarrow \ln \left(u(x)\right)
\end{align*}
\]
La fonction \(f\) est dérivable sur \(I\) et
\[
f'(x)=\frac{u'(x)}{u(x)}, \qquad \forall x\in I.
\]
Démonstration
On utilise le théorème de dérivation d'une fonction composée.
Soit \(v\) la fonction dérivable sur \(\mathbb{R}_{+}^{*}\) définie par \(v(x)=\ln(x)\). Nous avons \(f(x)=v\left(u(x)\right)\), et par suite : \[ \begin{align*} f'(x)&=\left(v\left(u(x)\right)\right)' \\ &=v'\left(u(x)\right)\times u'(x) \\ &=\frac{1}{u(x)}\times u'(x) \\ &=\frac{u'(x)}{u(x)} \end{align*} \]
On utilise le théorème de dérivation d'une fonction composée.
Soit \(v\) la fonction dérivable sur \(\mathbb{R}_{+}^{*}\) définie par \(v(x)=\ln(x)\). Nous avons \(f(x)=v\left(u(x)\right)\), et par suite : \[ \begin{align*} f'(x)&=\left(v\left(u(x)\right)\right)' \\ &=v'\left(u(x)\right)\times u'(x) \\ &=\frac{1}{u(x)}\times u'(x) \\ &=\frac{u'(x)}{u(x)} \end{align*} \]
IV) Logarithme décimal
Définition 3
On appelle fonction logarithme décimal la fonction notée \(\log_{10}\) ou \(\log\) qui, à tout réel strictement positif \(x,\) associe \(\log(x)\).
\[
\begin{align*}
\log : \mathbb{R}^{*}_{+}&\longrightarrow \mathbb{R} \\
x&\longrightarrow \frac{\ln(x)}{\ln(10)}
\end{align*}
\]
Les propriétés du logarithme décimal sont proches de celles du logarithme népérien. Nous les donnons rapidement ci-dessous.
Soient \(a\in \mathbb{R}^{*}_{+}\) et \(b\in \mathbb{R}^{*}_{+}\).
\(\log(1)=0\)
Démonstration
\[
\begin{align*}
\log(1)&=\frac{\ln(1)}{\ln(10)}\\
&=0
\end{align*}
\]
\(\log(a\times b)=\log(a)+\log(b)\)
Démonstration
\[
\begin{align*}
\log(a\times b)&=\frac{\ln\left(a\times b\right)}{\ln(10)}\\
&=\frac{\ln(a)+\ln(b)}{\ln(10)} \text{ (d'après la Propriété 3)} \\
&=\frac{\ln(a)}{\ln(10)}+\frac{\ln(b)}{\ln(10)}\\
&=\log(a)+\log(b) \text{ (d'après la Définition 3)}
\end{align*}
\]
\(\displaystyle \log \left(\frac{1}{a}\right)=-\log(a)\)
Démonstration
\[
\begin{align*}
\log \left(\frac{1}{a}\right)&=\frac{\ln \left(\frac{1}{a}\right)}{\ln(10)}\\
&=\frac{-\ln(a)}{\ln(10)} \text{ (d'après la Propriété 4)} \\
&=-\log(a) \text{ (d'après la Définition 3)}
\end{align*}
\]
\(\displaystyle \log \left(\frac{a}{b}\right)=\log(a)-\log(b)\)
Démonstration
\[
\begin{align*}
\log \left(\frac{a}{b}\right)&=\frac{\ln \left(\frac{a}{b}\right)}{\ln(10)}\\
&=\frac{\ln(a)-\ln(b)}{\ln(10)} \text{ (d'après la Propriété 5)} \\
&=\frac{\ln(a)}{\ln(10)}-\frac{\ln(b)}{\ln(10)}\\
&=\log(a)-\log(b) \text{ (d'après la Définition 3)}
\end{align*}
\]
\(\displaystyle \log (\sqrt{a})=\frac{1}{2}\log(a)\)
Démonstration
\[
\begin{align*}
\log (\sqrt{a})&=\frac{\ln (\sqrt{a})}{\ln(10)}\\
&=\frac{\frac{1}{2}\ln(a)}{\ln(10)} \text{ (d'après la Propriété 7)} \\
&=\frac{1}{2}\frac{\ln(a)}{\ln(10)}\\
&=\frac{1}{2}\log(a) \text{ (d'après la Définition 3)}
\end{align*}
\]
\(\log \left(a^{n}\right)=n\log(a), \; \forall n \in \mathbb{Z}\)
Démonstration
\[
\begin{align*}
\log \left(a^{n}\right)&=\frac{\ln \left(a^{n}\right)}{\ln(10)}\\
&=\frac{n\ln(a)}{\ln(10)} \text{ (d'après la Propriété 6)} \\
&=n\frac{\ln(a)}{\ln(10)}\\
&=n\log(a) \text{ (d'après la Définition 3)}
\end{align*}
\]
De manière plus générale, nous pouvons définir la fonction logarithme de base \(a\), notée \(\log_{a}\).
Définition 4
On appelle fonction logarithme de base \(a\) la fonction notée \(\log_{a}\) qui, à tout réel strictement positif \(x,\) associe \(\log_{a}(x)\).
\[
\begin{align*}
\log_{a} : \mathbb{R}^{*}_{+}&\longrightarrow \mathbb{R} \\
x&\longrightarrow \frac{\ln(x)}{\ln(a)}
\end{align*}
\]