LOGARITHME NEPERIEN
|
Exercice 1
\(\ln(3)+\ln(6)\)\(=\ln(3)+\ln(3\times 2)\)
\(=\ln(3)+\ln(3)+\ln(2)\)
\(=2\ln(3)+\ln(2)\)
\(\ln(10)-\ln(5)\)
\(=\ln(2\times 5)-\ln(5)\)
\(=\ln(2)+\ln(5)-\ln(5)\)
\(=\ln(2)\)
\(\ln(4)+\ln(8)-\ln(32)\)
\(=\ln(4)+\ln(8)-\ln(4\times 8)\)
\(=\ln(4)+\ln(8)-(\ln(4)+\ln(8))\)
\(=\ln(4)+\ln(8)-\ln(4)-\ln(8)\)
\(=0\)
\(\ln(e^{x})\)
\(=x\)
\(\ln\left(e^{x^{2}+2x+3}\right)\)
\(=x^{2}+2x+3\)
\(\displaystyle\ln\left(\frac{1}{x^{2}}\right)\)
\(=\ln(1)-\ln(x^{2})\)
\(=0-2\ln(x)\)
\(=-2\ln(x)\)
\(\ln\left(e^{-5}\right)\)
\(=-5\)
Exercice 2
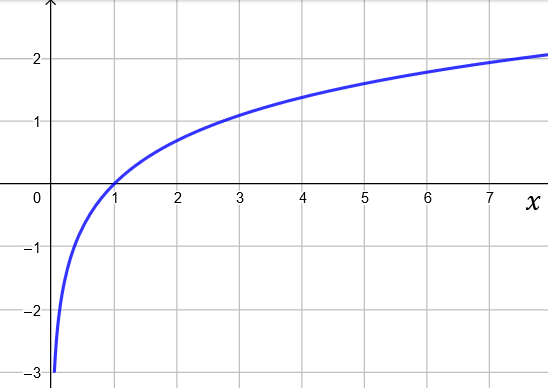
2) D'après le cours, nous avons : \[ \lim_{x\rightarrow 0^{+}} b(x)=-\infty \] \[ \lim_{x\rightarrow +\infty} b(x)=+\infty
\]
3)
\(b(x)=0 \)
\(\Leftrightarrow \ln(x)=0\)
\(\Leftrightarrow x=e^{0}\)
\(\Leftrightarrow x=1\)
\(b(x)=1\)
\(\Leftrightarrow \ln(x)=1\)
\(\Leftrightarrow x=e^{1}\)
\(\Leftrightarrow x=e\)
\(b(x)=4\)
\(\Leftrightarrow \ln(x)=4\)
\(\Leftrightarrow x=e^{4}\)
4) D'après le cours, la dérivée de la fonction \(b\) est \[ b'(x)=\frac{1}{x}. \]
5) Sur l'intervalle \(]0;+\infty[\), la fonction \(b\) est croissante car \(b'(x)>0\).
Exercice 3
\(A=\ln(2)+\ln(8)-\ln(4)\)\(\; \; \; \,=\ln(2)+\ln(2^{3})-\ln(2^{2})\)
\(\; \; \; \,=\ln(2)+3\ln(2)-2\ln(2)\)
\(\; \; \; \,=\ln(2)\left(1+3-2\right)\)
\(\; \; \; \,=2\ln(2)\)
\(B=\ln(3)+2\ln(27)\)
\(\; \; \; \,=\ln(3)+2\ln(3^{3})\)
\(\; \; \; \,=\ln(3)+2\times 3\times \ln(3)\)
\(\; \; \; \,=\ln(3)+6\ln(3)\)
\(\; \; \; \,=(1+6)\ln(3)\)
\(\; \; \; \,=7\ln(3)\)
\(C=-2\ln(5)+3\ln(25)\)
\(\; \; \; \,=-2\ln(5)+3\ln(5^{2})\)
\(\; \; \; \,=-2\ln(5)+3\times 2\times \ln(5)\)
\(\; \; \; \,=-2\ln(5)+6\ln(5)\)
\(\; \; \; \,=(-2+6)\ln(5)\)
\(\; \; \; \,=4\ln(5)\)
\(\displaystyle D=\frac{\ln(49)}{2}-5\ln(7)\)
\(\displaystyle \; \; \; \,=\frac{\ln(7^{2})}{2}-5\ln(7)\)
\(\displaystyle \; \; \; \,=\frac{2\ln(7)}{2}-5\ln(7)\)
\(\; \; \; \,=\ln(7)-5\ln(7)\)
\(\; \; \; \,=(1-5)\ln(7)\)
\(\; \; \; \,=-4\ln(7)\)
Exercice 4
\(\ln(x)=-2\)\(\Leftrightarrow x=e^{-2}\)
\(\displaystyle -3\ln(x)=\frac{3}{5}\)
\(\displaystyle \Leftrightarrow \ln(x)=\frac{3}{5\times (-3)}\)
\(\displaystyle \Leftrightarrow \ln(x)=-\frac{1}{5}\)
\(\displaystyle \Leftrightarrow x=e^{-\frac{1}{5}}\)
\(2e^{x}=-6\)
\(\displaystyle \Leftrightarrow e^{x}=\frac{-6}{2}\)
\(\Leftrightarrow e^{x}=-3\)
Cette équation n'a aucune solution, l'exponentielle d'un réel étant toujours positive.
\(4\ln(x)=-\ln(16)\)
\(\Leftrightarrow 4\ln(x)=-\ln(2^{4})\)
\(\Leftrightarrow 4\ln(x)=-4\ln(2)\)
\(\Leftrightarrow \ln(x)=-\ln(2)\)
\(\Leftrightarrow \ln(x)=\ln(1)-\ln(2)\)
\(\Leftrightarrow \displaystyle \ln(x)=\ln \left(\frac{1}{2}\right)\)
\(\Leftrightarrow \displaystyle x=\frac{1}{2}\)
\(\left(\ln(x)+4\right)\left(-2\ln(x)+6\right)=0\)
Ce produit est nul si au moins un de ses facteurs est nul. On a donc :
\(\ln(x)+4=0 \qquad \text{ ou } \qquad -2\ln(x)+6=0\)
\(\ln(x)=-4 \qquad \qquad \qquad \; \, -2\ln(x)=-6\)
\(x=e^{-4} \qquad \qquad \qquad \qquad \ln(x)=3\)
\(\qquad \qquad \qquad \qquad \qquad \quad \; \; x=e^{3}\)
Cette équation admet deux solutions : \(e^{-4}\) et \(e^{3}\).
\(\left(e^{x}-2\right)\left(e^{x}+3\right)=0\)
Ce produit est nul si au moins un de ses facteurs est nul. On a donc :
\(e^{x}-2=0 \qquad \text{ ou } \qquad e^{x}+3=0\)
\(e^{x}=2 \qquad \qquad \qquad \quad \; e^{x}=-3\)
L'exponentielle d'un réel étant toujours positive, l'équation \(e^{x}=-3\) n'admet aucune solution. La seule possibilité est d'avoir :
\(e^{x}=2\)
\(\Leftrightarrow x=\ln(2)\)
Cette équation admet une solution : \(\ln(2)\).
Exercice 5
\(\ln(x)\geq 5\)La fonction exponentielle étant croissante, nous avons
\(e^{\ln(x)}\geq e^{5}\)
\(x\geq e^{5}\)
Cette inégalité est vérifiée lorsque \(x\geq e^{5}\).
\(2\ln(x)\leq -4\)
\(\displaystyle \ln(x)\leq \frac{-4}{2}\)
\(\ln(x)\leq -2\)
La fonction exponentielle étant croissante, nous avons
\(e^{\ln(x)}\leq e^{-2}\)
\(x\leq e^{-2}\)
Cette inégalité est vérifiée lorsque \(x\leq e^{-2}\).
\(-\ln(x)> 2\)
\(\ln(x)<-2\)
La fonction exponentielle étant croissante, nous avons
\(e^{\ln(x)}< e^{-2}\)
\(x< e^{-2}\)
Cette inégalité est vérifiée lorsque \(x< e^{-2}\).
\(5\ln(x)< 10\)
\(\displaystyle \ln(x)\leq \frac{10}{5}\)
\(\ln(x)< 2\)
La fonction exponentielle étant croissante, nous avons
\(e^{\ln(x)}< e^{2}\)
\(x< e^{2}\)
Cette inégalité est vérifiée lorsque \(x< e^{2}\).