LOGARITHME NEPERIEN
|
Exercice 1
1) La fonction \(f\) est dérivable sur \(]0;+\infty[\), et sa dérivée est : \[ f'(x)=\frac{1}{x}-2. \] Nous remarquons que \(f'(x)>0\) lorsque \(x<0.5\), que \(f'(x)=0\) lorsque \(x=0.5\), et que \(f'(x)<0\) lorsque \(x>0.5\).De plus, nous avons : \[ \lim_{x\rightarrow 0^{+}} f(x)=-\infty, \] et \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \] En effet, nous pouvons réécrire \(f\) de la façon suivante : \[ f(x)=x \left[\frac{\ln(x)}{x}-2-\frac{3}{x}\right] \] Comme d'après le cours \[ \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x}=0, \] et \[ \lim_{x\rightarrow +\infty} \frac{3}{x}=0, \] nous avons \[ \lim_{x\rightarrow +\infty} \frac{\ln(x)}{x}-2-\frac{3}{x}=-2, \] et finalement : \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \] De plus, nous avons \[ \begin{align*} f(0.5)&=f\left(\frac{1}{2}\right)\\ &=\ln \left(\frac{1}{2}\right)-2\times \frac{1}{2}-3 \\ &=\ln(1)-\ln(2)-1-3 \\ &=-\ln(2)-4. \end{align*} \] Nous pouvons à présent réaliser le tableau de variations de la fonction \(f\) :
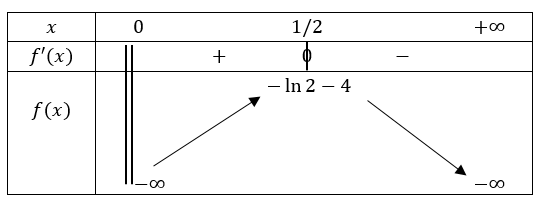
2) Le maximum de la fonction \(f\) est atteint en \(x=0.5\) et vaut \(-\ln(2)-4<0\). Par conséquent, il n'existe aucune solution à l'équation \(f(x)=2\).
3) La fonction \(f\) est continue et strictement croissante sur \(]0;0.5]\). De plus, \(\lim_{x\rightarrow 0^{+}}f(x)=-\infty\) et \(f(0.5)=-\ln(2)-4\approx -4.69\), donc d'après le théorème des valeurs intermédiaires, il existe une unique valeur \(\alpha \in ]0;0.5]\) telle que \(f(\alpha)=-10\).
D'autre part, la fonction \(f\) est continue et strictement décroissante sur \([0.5;+\infty[\). De plus, \(f(0.5)\approx -4.69\) et \(\lim_{x\rightarrow +\infty}f(x)=-\infty\), donc d'après le théorème des valeurs intermédiaires, il existe une unique valeur \(\beta \in [0.5;+\infty[\) telle que \(f(\beta)=-10\).
Conclusion : il y a deux solutions à l'équation \(f(x)=-10\) : \(\alpha \in ]0;0.5]\) et \(\beta \in [0.5;+\infty[\).
(On ne demandait pas de déterminer les valeurs de \(\alpha\) et de \(\beta\), simplement l'existence de solutions à cette équation.)
Exercice 2
1) L'équation de la tangente au point \(x=e\) est donnée par : \[ y=f(e)+f'(e)(x-e) \] Ici, avec \(\displaystyle f'(x)=\frac{1}{x}\), l'équation de la tangente \(\mathcal T\) à la courbe \(\mathcal C\) en \(e\) est donnée par \[ \begin{align*} y&=f(e)+\frac{1}{e}(x-e)\\ &=\ln(e)+\frac{x-e}{e}\\ &=1+\frac{x}{e}-1\\ &=\frac{x}{e} \end{align*} \]2) Représentation graphique
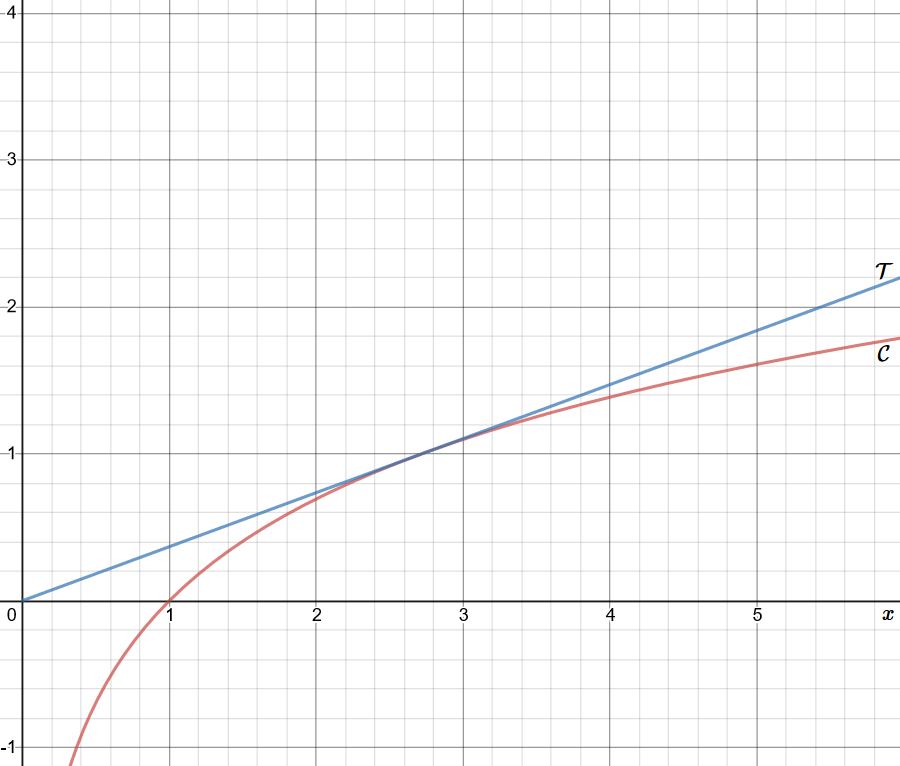
3) Il sufit de montrer que \(\forall x \in ]0;+\infty[\), \(z(x)=y-f(x)\geq 0\). \[ \begin{align*} z(x)&=y-f(x)\\ &=\frac{x}{e}-\ln(x) \end{align*} \] La fonction \(z\) est définie et dérivable sur \(\mathbb{R}^{*}_{+}\), et sa dérivée est : \[ z'(x)=\frac{1}{e}-\frac{1}{x} \] Nous avons \(z'(x)<0\) lorsque \(x\in ]0;e[\), \(z'(x)=0\) lorsque \(x=e\), et \(z'(x)>0\) lorsque \(x>e\). De plus : \[ \lim_{x\rightarrow 0^{+}}z(x)=+\infty, \] et \[ \lim_{x\rightarrow +\infty}z(x)=+\infty. \] Nous pouvons réaliser à présent le tableau de variations de la fonction \(z\).
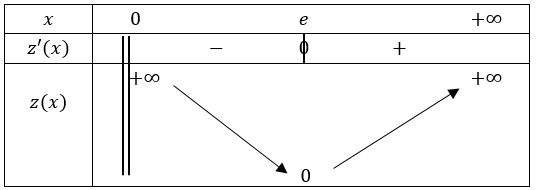
D'après le tableau de variations, nous avons \(z(x)\geq 0\), \(\forall x \in \mathbb{R}^{*}_{+}\). Par conséquent, la tangente \(\mathcal T\) est située au-dessus de \(\mathcal C\) sur \(]0;+\infty[\).
Exercice 3
\( \ln(42)\)\(= \ln(2\times 3 \times 7)\)
\(=\ln(2)+\ln(3)+\ln(7)\)
\(\displaystyle \ln \left(\frac{35}{6}\right)\)
\(=\ln(35)-\ln(6)\)
\(=\ln(7\times 5)-\ln(3\times 2)\)
\(=\ln(7)+\ln(5)-\ln(3)-\ln(2)\)
\( \ln \left(\sqrt{14}\right)\)
\(=\ln \left(14^{1/2}\right)\)
\(\displaystyle=\frac{1}{2}\ln \left(14\right)\)
\(\displaystyle=\frac{1}{2}\ln \left(7\times 2\right)\)
\(\displaystyle=\frac{1}{2}\left(\ln(7)+\ln(2)\right)\)
\( \ln \left(\sqrt{70}\right)-\ln \left(\sqrt{10}\right) \)
\(\displaystyle =\frac{1}{2}\ln(70)-\frac{1}{2}\ln(10)\)
\(\displaystyle =\frac{1}{2}\left(\ln(70)-\ln(10)\right)\)
\(\displaystyle =\frac{1}{2}\times \ln \left(\frac{70}{10}\right)\)
\(\displaystyle =\frac{1}{2}\times \ln(7)\)
Exercice 4
\(\ln(3x+2)=2\ln(2)\)\(\Leftrightarrow \ln(3x+2)=\ln(2^{2})\)
\(\Leftrightarrow \ln(3x+2)=\ln(4)\)
\(\Leftrightarrow 3x+2=4\)
\(\Leftrightarrow 3x=2\)
\(\displaystyle \Leftrightarrow x=\frac{2}{3}\)
\(\displaystyle \ln \left(\frac{51}{x}\right)=3\ln(3)\)
\(\displaystyle \Leftrightarrow \ln \left(\frac{51}{x}\right)=\ln(3^{3})\)
\(\displaystyle \Leftrightarrow \ln \left(\frac{51}{x}\right)=\ln(27)\)
\(\displaystyle \Leftrightarrow \frac{51}{x}=27\)
\(\displaystyle \Leftrightarrow x=\frac{51}{27}\)
\(\ln(4x)-\ln(2x-1)=0\)
\(\Leftrightarrow \ln(4x)=\ln(2x-1)\)
Il faut que \(4x>0\) d'une part, et \(2x-1>0\) d'autre part, ou encore \(x>0\) et \(\displaystyle x>\frac{1}{2}\).
Autrement dit, s'il existe au moins une solution, celle-ci doit être supérieure à \(\displaystyle \frac{1}{2}\).
Or l'équation \(4x=2x-1\) admet une unique solution, \(\displaystyle x=-\frac{1}{2}<\frac{1}{2}\). Par conséquent, il n'y a pas de solution à l'équation \(\ln(4x)-\ln(2x-1)=0\).
\(\ln(5x+1)\leq 11\)
La partie à gauche de l'inégalité implique d'avoir \(\displaystyle x>-\frac{1}{5}\).
\(\Leftrightarrow 5x+1\leq e^{11}\)
\(\Leftrightarrow \displaystyle x\leq \frac{e^{11}-1}{5}\)
Par conséquent, les valeurs de \(x\) qui sont solutions de cette inéquation sont : \[ x \in \left]-\frac{1}{5};\frac{e^{11}-1}{5} \right] \]
\(\ln(2x)\geq \ln(4-x)\)
Il faut que \(2x>0\) d'une part, et \(4-x>0\) d'autre part, ou encore \(x>0\) et \(\displaystyle x<4\).
Autrement dit, s'il existe au moins une solution, celle-ci doit appartenir à l'intervalle \(]0;4[\).
Nous avons :
\(2x \geq 4-x\)
\(\Leftrightarrow \displaystyle x \geq \frac{4}{3}\)
Par conséquent, les valeurs de \(x\) qui sont solutions de l'inéquation \(\ln(2x)\geq \ln(4-x)\) sont : \[ x \in \left[\frac{4}{3};4 \right[ \]
\(\left(\ln(x)\right)^{2}+5\ln(x)=-4\)
\( \Leftrightarrow \left(\ln(x)\right)^{2}+5\ln(x)+4=0\)
On pose \(X=\ln(x)\). L'équation s'écrit :
\(X^{2}+5X+4=0\)
On reconnaît un polynôme du second degré. Le calcul du discriminant donne :
\(\Delta=5^{2}-4\times 1\times 4=9\)
L'équation \(X^{2}+5X+4=0\) admet deux solutions : \[ \begin{align*} X_{1}&=\frac{-5-\sqrt{9}}{2}=-4 \\ X_{2}&=\frac{-5+\sqrt{9}}{2}=-1 \end{align*} \] Comme nous avons posé \(X=\ln(x)\), lorsque \(X_{1}=-4\) alors \(x_{1}=e^{-4}\), et lorsque \(X_{2}=-1\) alors \(\displaystyle x_{2}=e^{-1}=\frac{1}{e}\).
L'équation \(\left(\ln(x)\right)^{2}+5\ln(x)=-4\) admet deux solutions : \(e^{-4}\) et \(\displaystyle \frac{1}{e}\).
Exercice 5
1) Par définition du nombre dérivé de la fonction \(\ln\) en 1, nous avons \[ \begin{align*} \lim_{x\rightarrow 0}\frac{\ln(x+1)}{x}&=\lim_{x\rightarrow 0}\frac{\ln(1+x)-\ln(1)}{x} \\ &=1 \end{align*} \] 2) On utilise ici les résultats de la question 1.
a) En posant \(X=x^{2}\), lorsque \(x\) tend vers 0, il en est de même pour \(X\), et nous avons alors :
\[
\lim_{x\rightarrow 0}\frac{\ln(x^{2}+1)}{x^{2}}=\lim_{X\rightarrow 0}\frac{\ln(X+1)}{X}=1.
\]
b) En posant \(X=\sqrt{x}\), lorsque \(x\) tend vers 0, il en est de même pour \(X\), et nous avons alors :
\[
\lim_{x\rightarrow 0}\frac{\ln(\sqrt{x}+1)}{\sqrt{x}}=\lim_{X\rightarrow 0}\frac{\ln(X+1)}{X}=1.
\]
Exercice 6
\(f(x)=\ln(3x)-x^{2}+1\)La fonction \(f\) est définie sur \(\mathbb{R}_{+}^{*}\) et est dérivable sur ce même intervalle. Sa dérivée est \[ f'(x)=\frac{3}{3x}-2x=\frac{1}{x}-2x. \]
\(g(x)=\ln(3x^{2})\)
La fonction \(g\) est définie sur \(\mathbb{R}_{+}^{*}\) et est dérivable sur ce même intervalle. Sa dérivée est \[ g'(x)=\frac{6x}{3x^{2}}=\frac{2}{x}. \]
\(h(x)=\ln(x^{2}-1)\)
La fonction \(h\) est définie lorsque \(x^{2}-1>0\), c'est à dire lorsque \(x \in ]-\infty;-1[\cup ]1;+\infty[\).
Elle est dérivable sur ce même intervalle, et de dérivée \[ h'(x)=\frac{2x}{x^{2}-1}. \]
\(\displaystyle i(x)=\frac{\ln(x^{2}-4)}{\ln(x-e)}\)
La fonction \(i\) est définie lorsque \(x^{2}-4>0\) et lorsque \(x>e\). La première condition implique \(x \in ]-\infty;-2[\cup ]2;+\infty[\), et la seconde \(x \in ]e;+\infty[\). La fonction \(i\) est définie sur l'intersection de ces intervalles, c'est à dire sur \(]e;+\infty[\).
La fonction \(i\) est dérivable sur ce même intervalle, et sa dérivée est :
\[ i'(x)=\frac{\frac{2x}{x^{2}-4}\ln(x-e)-\ln(x^{2}-4)\frac{1}{x-e}}{\left(\ln(x-e)\right)^{2}} \]
\(\displaystyle j(x)=\frac{\ln(1+\sqrt{x-1})}{x^{2}-1}\)
La fonction \(j\) est définie lorsque \(x^{2}-1\neq 0\), \(\sqrt{x-1}\geq 0\) et \(1+\sqrt{x-1}>0\).
La première condition implique \(x\neq -1\) et \(x \neq 1\).
La deuxième condition implique \(x\geq 1\).
La troisième condition est toujours vérifiée du moment que la seconde condition l'est.
La fonction \(j\) est définie sur l'intersection de ces intervalles, c'est à dire sur \(]1;+\infty[\).
La fonction \(j\) est dérivable sur ce même intervalle, et sa dérivée est : \[ j'(x)=\frac{\frac{1}{2\sqrt{x-1}}(x^{2}-1)-\ln(1+\sqrt{x-1})\times 2x}{\left(x^{2}-1\right)^{2}} \]