FONCTIONS TRIGONOMETRIQUES
|
Exercice 1 (Nouvelle-Calédonie décembre 2019 (extrait))
Partie COn considère la fonction \(f\) définie sur \([0;2\pi]\) par \[ f(x)=-1.5\cos(x)+1.5. \] On admet que la fonction \(f\) est continue sur \([0;2\pi]\).
On note \(\mathcal{C}_{1}\) la courbe représentative de la fonction \(f\) dans un repère orthonormé.
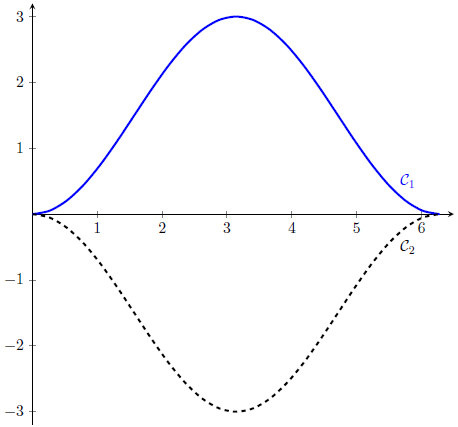
1) Démontrer que la fonction \(f\) est positive sur \([0 ; 2\pi]\).
2) Sur la figure ci-dessus, la courbe tracée en tiretés, notée \(\mathcal{C}_{2}\), est la courbe symétrique de \(\mathcal{C}_{1}\) par rapport à l’axe des abscisses.
La forme d’un carreau est celle de la zone délimitée par les courbes \(\mathcal{C}_{1}\) et \(\mathcal{C}_{2}\).
On note \(\mathcal{A}\) son aire, exprimée en unité d’aire.
Calculer \(\mathcal{A}\).
Exercice 2 (Antilles Guyane juin 2018)
Un publicitaire souhaite imprimer le logo ci-dessous sur un T-shirt :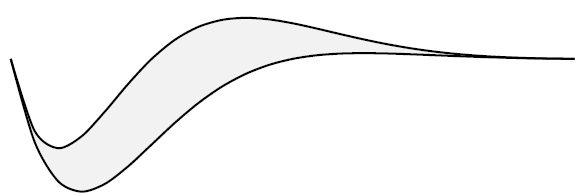
Il dessine ce logo à l’aide des courbes de deux fonctions \(f\) et \(g\) définies sur \(\mathbb{R}\) par : \[ f(x)=e^{-x}\left(-\cos(x)+\sin(x)+1\right) \] et \[ g(x)=-e^{-x}\cos(x). \] On admet que les fonctions \(f\) et \(g\) sont dérivables sur \(\mathbb{R}\).
Partie A : Étude de la fonction \(f\)
1) Justifier que, pour tout \(x\in \mathbb{R}\) : \[ −e^{−x}\leq f(x) \leq 3e^{−x}. \] 2) En déduire la limite de \(f\) en \(+\infty\).
3) Démontrer que, pour tout \(x\in \mathbb{R}\), \(f′(x)=e^{−x}(2\cos x−1)\) où \(f′\) est la fonction dérivée de \(f\).
4) Dans cette question, on étudie la fonction \(f\) sur l’intervalle \([−\pi;\pi]\).
a) Déterminer le signe de \(f′(x)\) pour \(x\) appartenant à l’intervalle \([−\pi;\pi]\).
b) En déduire les variations de \(f\) sur \([−\pi;\pi]\).
b) En déduire les variations de \(f\) sur \([−\pi;\pi]\).
Partie B : Aire du logo
On note \(\mathcal{C}_{f}\) et \(\mathcal{C}_{g}\) les représentations graphiques des fonctions \(f\) et \(g\) dans un repère orthonormé \(\left(O;\vec{i},\vec{j}\right)\).
L’unité graphique est de 2 centimètres. Ces deux courbes sont tracées ci-dessous.
1) Étudier la position relative de la courbe \(\mathcal{C}_{f}\) par rapport à la courbe \(\mathcal{C}_{g}\) sur \(\mathbb{R}\).
2) Soit \(H\) la fonction définie sur \(\mathbb{R}\) par : \[ H(x)=\left(-\frac{\cos x}{2}-\frac{\sin x}{2}-1\right)e^{-x}. \] On admet que \(H\) est une primitive de la fonction \(x\rightarrow (\sin x+1)e^{-x}\) sur \(\mathbb{R}\).
On note \(\mathcal{D}\) le domaine délimité par la courbe \(\mathcal{C}_{f}\), la courbe \(\mathcal{C}_{g}\) et les droites d’équation \(\displaystyle x=-\frac{\pi}{2}\) et \(\displaystyle x=\frac{3\pi}{2}\).
a) Hachurer le domaine \(\mathcal{D}\) sur le graphique à rendre avec la copie.
b) Calculer, en unité d’aire, l’aire du domaine \(\mathcal{D}\), puis en donner une valeur approchée à \(10^{−2}\) près en cm2.
b) Calculer, en unité d’aire, l’aire du domaine \(\mathcal{D}\), puis en donner une valeur approchée à \(10^{−2}\) près en cm2.
Exercice 3 (Métropole - La Réunion juin 2016)
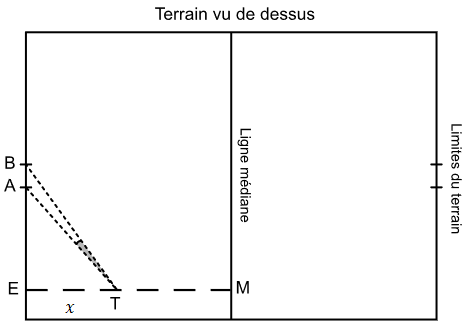Lors d’un match de rugby, un joueur doit transformer un essai qui a été marqué au point \(E\) (voir figure ci-contre) situé à l’extérieur du segment \([AB]\). La transformation consiste à taper le ballon par un coup de pied depuis un point \(T\) que le joueur a le droit de choisir n’importe où sur le segment \([EM]\) perpendiculaire à la droite \((AB)\) sauf en \(E\). La transformation est réussie si le ballon passe entre les poteaux repérés par les points \(A\) et \(B\) sur la figure.
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point \(T\) qui rend l’angle \(\widehat{ATB}\) le plus grand possible.
Le but de cet exercice est donc de rechercher s’il existe une position du point \(T\) sur le segment \([EM]\) pour laquelle l’angle \(\widehat{ATB}\) est maximum et, si c’est le cas, de déterminer une valeur approchée de cet angle.
Dans toute la suite, on note \(x\) la longueur \(ET\), qu’on cherche à déterminer.
Les dimensions du terrain sont les suivantes : \(EM = 50\text{m}\), \(EA = 25\text{m}\) et \(AB = 5,6\text{m}\). On note \(\alpha\) la mesure en radian de l’angle \(\widehat{ETA}\), \(\beta\) la mesure en radian de l’angle \(\widehat{ETB}\) et \(\gamma\) la mesure en radian de l’angle \(\widehat{ATB}\).
1) En utilisant les triangles rectangles \(ETA\) et \(ETB\) ainsi que les longueurs fournies, exprimer \(\tan\alpha\) et \(\tan\beta\) en fonction de \(x\).
La fonction tangente est définie sur l’intervalle \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\) par \(\displaystyle \tan x=\frac{\sin x}{\cos x}\).
2) Montrer que la fonction \(\tan\) est strictement croissante sur l’intervalle \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\).
3) L’angle \(\widehat{ATB}\) admet une mesure \(\gamma\) appartenant à l’intervalle \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\), résultat admis ici, que l’on peut observer sur la figure.
On admet que, pour tous réels \(a\) et \(b\) de l’intervalle \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\), \[ \tan(a-b)=\frac{\tan a-\tan b}{1+\tan a \times \tan b}. \] Montrer que \(\displaystyle \tan \gamma=\frac{5.6x}{x^{2}+765}.\)
4) L’angle \(\widehat{ATB}\) est maximum lorsque sa mesure \(\gamma\) est maximale.
Montrer que cela correspond à un minimum sur l’intervalle \(]0; 50]\) de la fonction \(f\) définie par : \[ f(x)=x+\frac{765}{x}. \] Montrer qu’il existe une unique valeur de \(x\) pour laquelle l'angle \(\widehat{ATB}\) est maximum et déterminer cette valeur de \(x\) au mètre près ainsi qu’une mesure de l'angle \(\widehat{ATB}\) à 0.01 radian près.
Exercice 4 (Polynésie septembre 2015 (extrait))
Partie BDans cette partie, on admet que, pour tout réel \(\theta\), \(\displaystyle \cos(\theta)+\sin(\theta)=\sqrt{2}\cos \left(\theta−\frac{\pi}{4}\right)\).
On considère les fonctions \(f\) et \(g\) définies sur l’intervalle \([0 ;+\infty[\) par : \[ f(x)=e^{-x}\cos(x) \] et \[ g(x)=e^{-x}. \] On définit la fonction \(h\) sur \([0 ;+\infty[\) par \(h(x)=g(x)−f(x)\).
Les représentations graphiques \(\mathscr{C}_{f}\), \(\mathscr{C}_{g}\) et \(\mathscr{C}_{h}\) des fonctions \(f\), \(g\) et \(h\) sont données ci-dessous, dans un repère orthogonal.
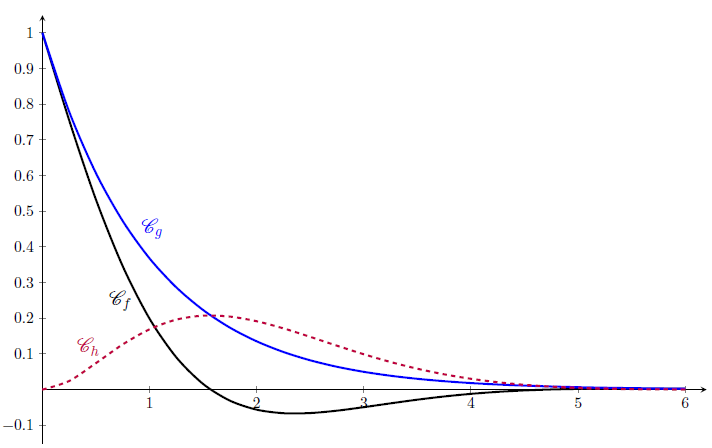
1) Conjecturer :
a) les limites des fonctions \(f\) et \(g\) en \(+\infty\) ;
b) la position relative de \(\mathscr{C}_{f}\) par rapport à \(\mathscr{C}_{g}\) ;
c) la valeur de l’abscisse \(x\) pour laquelle l’écart entre les deux courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\) est maximal.
2) Justifier que \(\mathscr{C}_{g}\) est située au-dessus de \(\mathscr{C}_{f}\) sur l’intervalle \([0 ;+\infty[\). b) la position relative de \(\mathscr{C}_{f}\) par rapport à \(\mathscr{C}_{g}\) ;
c) la valeur de l’abscisse \(x\) pour laquelle l’écart entre les deux courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\) est maximal.
3) Démontrer que la droite d’équation \(y=0\) est asymptote horizontale aux courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\).
4)
a) On note \(h′\) la fonction dérivée de la fonction \(h\) sur l’intervalle \([0 ;+\infty[\).
Démontrer que, pour tout \(x\) de l’intervalle \([0 ;+\infty[\), \[ h'(x)=e^{-x}\left[\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right]. \] b) Justifier que, sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\), \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0\) et que, sur l'intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\), \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0\).
c) En déduire le tableau de variation de la fonction \(h\) sur l’intervalle \([0 ; 2\pi]\).
5) On admet que, sur l’intervalle \([0 ;+\infty[\), la fonction \(H\) définie par
\[
H(x)=\frac{1}{2}e^{-x}\left[-2+\cos(x)-\sin(x)\right]
\]
est une primitive de la fonction \(h\). Démontrer que, pour tout \(x\) de l’intervalle \([0 ;+\infty[\), \[ h'(x)=e^{-x}\left[\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right]. \] b) Justifier que, sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\), \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0\) et que, sur l'intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\), \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0\).
c) En déduire le tableau de variation de la fonction \(h\) sur l’intervalle \([0 ; 2\pi]\).
On note \(\mathscr{D}\) le domaine du plan délimité par les courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\), et les droites d’équations \(x=0\) et \(x=2\pi\).
Calculer l’aire \(\mathscr{A}\) du domaine \(\mathscr{D}\), exprimée en unités d’aire.
Exercice 5 (Nouvelle-Calédonie novembre 2015 (extrait))
Partie CLe service commercial a adopté pour les étiquettes des bouteilles la forme représentée ci-dessous dans un repère orthonormé du plan.
La forme de ces étiquettes est délimitée par l’axe des abscisses et la courbe \(\mathscr{C}\) d’équation \(y=a\cos x\) avec \(\displaystyle x \in \left[−\frac{\pi}{2};\frac{\pi}{2}\right]\) et \(a\) un réel strictement positif.
Un disque situé à l’intérieur est destiné à recevoir les informations données aux acheteurs. On considère le disque de centre le point \(A\) de coordonnées \(\displaystyle \left(0 ;\frac{a}{2}\right)\) et de rayon \(\displaystyle \frac{a}{2}\). On admettra que ce disque se trouve entièrement en dessous de la courbe \(\mathscr{C}\) pour des valeurs de \(a\) inférieures à 1,4.
1) Justifier que l’aire du domaine compris entre l’axe des abscisses, les droites d’équation \(\displaystyle x=-\frac{\pi}{2}\) et \(\displaystyle x=\frac{\pi}{2}\), et la courbe \(\mathscr{C}\) est égale à \(2a\) unités d’aire.
2) Pour des raisons esthétiques, on souhaite que l’aire du disque soit égale à l’aire de la surface grisée. Quelle valeur faut-il donner au réel \(a\) pour respecter cette contrainte ?