FONCTIONS TRIGONOMETRIQUES
|
I) Rappels
A) Le cercle trigonométrique
Définition 1
Dans le plan muni du repère orthonormé \(\left(0;\vec{i};\vec{j}\right)\), on appelle cercle trigonométrique le cercle de centre \(O\) et de rayon 1 orienté dans le sens direct (appelé encore sens trigonométrique ou sens positif).
Le sens direct est le sens contraire de la rotation des aiguilles d'une montre.
Le sens indirect (ou encore sens négatif) est le sens de la rotation des aiguilles d'une montre.
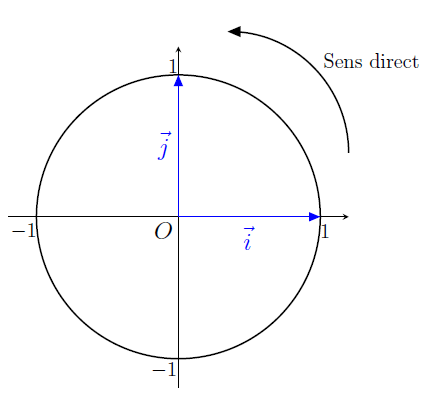
Plaçons les points \(A(1;0)\) et \(B(0;1)\).
Sur le graphique ci-dessous (partie gauche), nous avons tracé l'axe des réels (en violet).
Imaginons que l'on enroule l'axe des réels autour du cercle trigonométrique (graphique ci-dessous, partie droite).
Sur le graphique ci-dessous (partie gauche), nous avons tracé l'axe des réels (en violet).
Imaginons que l'on enroule l'axe des réels autour du cercle trigonométrique (graphique ci-dessous, partie droite).

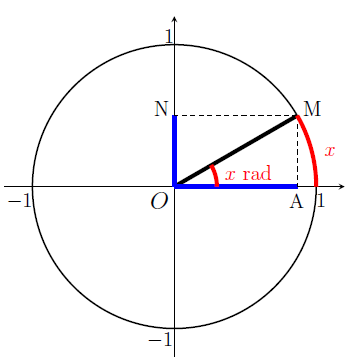
On constate tout d'abord que le réel 0 est associé à un unique point : le point \(A\).
On constate également que le réel \(\displaystyle \frac{\pi}{2}\approx 1.57\) est associé à un unique point : le point B.
En effet, le périmètre du cercle est égal à \(2\pi R\) avec \(R\) le rayon. Ici, le rayon vaut 1 donc le périmètre du cercle est égal à \(2\pi\).
Lorsqu'on parcourt sur le cercle la distance entre le point A et le point B, on effectue un quart de cercle. Par conséquent, la longueur de l'arc de cercle entre A et B est égale à \(\displaystyle \frac{2\pi}{4}=\frac{\pi}{2}\).
En fait, pour tout réel \(x\), on peut associer un unique point du cercle trigonométrique.
Par contre, pour tout point du cercle trigonométrique, on peut associer une infinité de réels.
Par exemple, reprenons le point \(A\). Nous avons vu précédemment qu'il est associé au réel 0.
Mais il est tout à fait possible d'enrouler l'axe des réels (la partie positive) autout du cercle trigonométrique en faisant un tour complet du cercle.
Le périmètre du cercle mesurant \(2\pi\), cela signifie que le point A est aussi associé au réel \(2\pi\).
Au lieu de faire un seul tour de cercle, je pourrais en effectuer deux, et par conséquent le point A est aussi associé au réel \(4\pi\), ainsi de suite...
Si on enroule la partie négative de l'axe des réels autour du cercle trigonométrique en effectuant un tour complet, alors le point A est aussi associé au réel \(-2\pi\).
Si c'est deux tours complets, alors le point A est aussi associé au réel \(-4\pi\), et ainsi de suite.
En fait, pour n'importe quel point \(M\) du cercle trigonométrique associé à un réel \(x_{0}\), nous pouvons donner tous les réels associés au point M.
On constate également que le réel \(\displaystyle \frac{\pi}{2}\approx 1.57\) est associé à un unique point : le point B.
En effet, le périmètre du cercle est égal à \(2\pi R\) avec \(R\) le rayon. Ici, le rayon vaut 1 donc le périmètre du cercle est égal à \(2\pi\).
Lorsqu'on parcourt sur le cercle la distance entre le point A et le point B, on effectue un quart de cercle. Par conséquent, la longueur de l'arc de cercle entre A et B est égale à \(\displaystyle \frac{2\pi}{4}=\frac{\pi}{2}\).
En fait, pour tout réel \(x\), on peut associer un unique point du cercle trigonométrique.
Par contre, pour tout point du cercle trigonométrique, on peut associer une infinité de réels.
Par exemple, reprenons le point \(A\). Nous avons vu précédemment qu'il est associé au réel 0.
Mais il est tout à fait possible d'enrouler l'axe des réels (la partie positive) autout du cercle trigonométrique en faisant un tour complet du cercle.
Le périmètre du cercle mesurant \(2\pi\), cela signifie que le point A est aussi associé au réel \(2\pi\).
Au lieu de faire un seul tour de cercle, je pourrais en effectuer deux, et par conséquent le point A est aussi associé au réel \(4\pi\), ainsi de suite...
Si on enroule la partie négative de l'axe des réels autour du cercle trigonométrique en effectuant un tour complet, alors le point A est aussi associé au réel \(-2\pi\).
Si c'est deux tours complets, alors le point A est aussi associé au réel \(-4\pi\), et ainsi de suite.
En fait, pour n'importe quel point \(M\) du cercle trigonométrique associé à un réel \(x_{0}\), nous pouvons donner tous les réels associés au point M.
Propriété 1
Pour tout point \(M\) du cercle trigonométrique associé à un réel \(x_{0}\) sont associés tous les réels de la forme \(x_{0}+2k\pi\), avec \(k\in \mathbb{Z}\).
En revenant à notre exemple, le point A est associé au réel \(0\) mais également aux réels \(2\pi\), \(4\pi\), \(6\pi\)... mais aussi \(-2\pi\), \(-4\pi\), \(-6\pi\)...
Le point B est associé au réel \(\displaystyle \frac{\pi}{2}\) mais également aux réels \(\displaystyle \frac{5\pi}{2}\), \(\displaystyle \frac{9\pi}{2}\), \(\displaystyle \frac{13\pi}{2}\)... mais aussi \(\displaystyle -\frac{3\pi}{2}\), \(\displaystyle -\frac{7\pi}{2}\), \(\displaystyle -\frac{11\pi}{2}\)...
Le point B est associé au réel \(\displaystyle \frac{\pi}{2}\) mais également aux réels \(\displaystyle \frac{5\pi}{2}\), \(\displaystyle \frac{9\pi}{2}\), \(\displaystyle \frac{13\pi}{2}\)... mais aussi \(\displaystyle -\frac{3\pi}{2}\), \(\displaystyle -\frac{7\pi}{2}\), \(\displaystyle -\frac{11\pi}{2}\)...
Dans la partie qui suit, nous rappelons la définition du cosinus et du sinus.
B) Cosinus et sinus d'un nombre réel
Définition 2
Dans le plan muni du repère orthonormé \(\left(0;\vec{i};\vec{j}\right)\), soit \(x\) un réel et \(M\) le point du cercle trigonométrique associé à ce réel \(x\).
Alors les coordonnées du point \(M\) sont \((\cos(x);\sin(x))\).
Alors les coordonnées du point \(M\) sont \((\cos(x);\sin(x))\).
C) Formules trigonométriques
Propriété 2
Pour tout réel \(x\) :
\[
\cos^{2}(x)+\sin^{2}(x)=1.
\]
Sur le graphique précédent, nous visualisons que les coordonnées (abscisse et ordonnée) du point \(M\) appartenant à ce cercle sont nécessairement comprises entre -1 et 1. Nous avons ainsi la propriété suivante.
Propriété 3
Pour tout réel \(x\) :
\[
\begin{align*}
&-1\leq \cos(x) \leq 1
&-1\leq \sin(x) \leq 1.
\end{align*}
\]
Il existe quelques valeurs remarquables concernant le cosinus et le sinus d'un angle. Celles-ci sont résumées dans le tableau ci-dessous.
| \(x\) | \(0\) | \(\displaystyle \frac{\pi}{6}\) | \(\displaystyle \frac{\pi}{4}\) | \(\displaystyle \frac{\pi}{3}\) | \(\displaystyle \frac{\pi}{2}\) |
| \(\displaystyle \cos(x)\) | \(1\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{1}{2}\) | \(0\) |
| \(\displaystyle \sin(x)\) | \(0\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(1\) |
Démonstration
Considérons le schéma ci-dessous :

a) \(x=0\)
Le point \(A\) du cercle trigonométrique associé au réel \(x=0\) a pour coordonnées \((1;0)\).
Or d'après la Définition 2, lorsque \(x=0\) les coordonnées du point \(A\) sont \(\left(\cos(0);\sin(0)\right)\).
On en déduit ainsi \(\cos(0)=1\) et \(\sin(0)=0\).
b) \(x=\displaystyle \frac{\pi}{2}\)
Le point \(B\) du cercle trigonométrique associé au réel \(x=\displaystyle \frac{\pi}{2}\) a pour coordonnées \((0;1)\).
En effet, étant donné que le périmètre du cercle est égal à \(2\pi\), cela signifie que l'on effectue un quart de tour dans le sens inverse des aiguilles d'une montre en partant du point \(A\) pour arriver au point \(B\).
Or d'après la Définition 2, lorsque \(x=\displaystyle \frac{\pi}{2}\) les coordonnées du point \(B\) sont \(\displaystyle \left(\cos \left(\frac{\pi}{2}\right);\sin \left(\frac{\pi}{2}\right)\right)\).
On en déduit ainsi \(\displaystyle \cos \left(\frac{\pi}{2}\right)=0\) et \(\displaystyle \sin \left(\frac{\pi}{2}\right)=1\).
c) \(x=\displaystyle \frac{\pi}{4}\)
Nous savons que la somme des angles d'un triangle est égale à 180 degrés, soit \(\pi\) radians.
Si on considère le triangle OYC rectangle en Y, étant donné que nous avons \(\displaystyle \widehat{OYC}=90^{°}=\frac{\pi}{2}\text{ rad,}\) nous en déduisons que l'angle \(\widehat{OCY}\) mesure : \[ \begin{align*} \widehat{OCY}&=\pi - \widehat{OYC} - \widehat{YOC} \\ &=\pi - \frac{\pi}{2}-\frac{\pi}{4}\\ &=\frac{\pi}{4}\text{ rad}. \end{align*} \] Ainsi, nous avons \(\displaystyle \widehat{OCY}=\widehat{YOC}=\frac{\pi}{4}\text{ rad,}\) donc le triangle OYC est isocèle rectangle en Y, et finalement \(OY=OC\).
Etant donné que \(OY=OC\) et que le repère est orthonormé, cela signifie que l'abscisse et l'ordonnée du point \(C\) sont identiques. Comme \(C\) a pour coordonnées \(\left(\cos \left(\frac{\pi}{4}\right);\sin\left(\frac{\pi}{4}\right)\right),\) on en déduit que : \[ \cos \left(\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}\right). \] En utilisant la Propriété 2 lorsque \(\displaystyle x=\frac{\pi}{4},\) nous avons : \[ \begin{align*} &\cos^{2}\left(\frac{\pi}{4}\right)+\sin^{2}\left(\frac{\pi}{4}\right)=1 \\ \Longleftrightarrow & \cos^{2}\left(\frac{\pi}{4}\right)+\cos^{2}\left(\frac{\pi}{4}\right)=1 \text{ car } \cos \left(\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}\right)\\ \Longleftrightarrow & 2\cos^{2}\left(\frac{\pi}{4}\right)=1 \\ \Longleftrightarrow & \cos^{2}\left(\frac{\pi}{4}\right)=\frac{1}{2} \end{align*} \] Etant donné que le cosinus est positif (compris entre 0 et 1), cette dernière équation admet une unique solution : \[ \begin{align*} \cos\left(\frac{\pi}{4}\right)&=\sqrt{\frac{1}{2}}\\ &=\frac{1}{\sqrt{2}}\\ &=\frac{\sqrt{2}}{\sqrt{2}\times \sqrt{2}}\\ &=\frac{\sqrt{2}}{2}. \end{align*} \] Finalement : \[ \cos\left(\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}. \]
d) Les démonstrations lorsque \(x=\displaystyle \frac{\pi}{6}\) et \(x=\displaystyle \frac{\pi}{3}\) font l'objet de deux exercices corrigés que vous pourrez retrouver dans les feuilles d'exercices d'entraînement (Exercice 1 et 2).
Considérons le schéma ci-dessous :

a) \(x=0\)
Le point \(A\) du cercle trigonométrique associé au réel \(x=0\) a pour coordonnées \((1;0)\).
Or d'après la Définition 2, lorsque \(x=0\) les coordonnées du point \(A\) sont \(\left(\cos(0);\sin(0)\right)\).
On en déduit ainsi \(\cos(0)=1\) et \(\sin(0)=0\).
b) \(x=\displaystyle \frac{\pi}{2}\)
Le point \(B\) du cercle trigonométrique associé au réel \(x=\displaystyle \frac{\pi}{2}\) a pour coordonnées \((0;1)\).
En effet, étant donné que le périmètre du cercle est égal à \(2\pi\), cela signifie que l'on effectue un quart de tour dans le sens inverse des aiguilles d'une montre en partant du point \(A\) pour arriver au point \(B\).
Or d'après la Définition 2, lorsque \(x=\displaystyle \frac{\pi}{2}\) les coordonnées du point \(B\) sont \(\displaystyle \left(\cos \left(\frac{\pi}{2}\right);\sin \left(\frac{\pi}{2}\right)\right)\).
On en déduit ainsi \(\displaystyle \cos \left(\frac{\pi}{2}\right)=0\) et \(\displaystyle \sin \left(\frac{\pi}{2}\right)=1\).
c) \(x=\displaystyle \frac{\pi}{4}\)
Nous savons que la somme des angles d'un triangle est égale à 180 degrés, soit \(\pi\) radians.
Si on considère le triangle OYC rectangle en Y, étant donné que nous avons \(\displaystyle \widehat{OYC}=90^{°}=\frac{\pi}{2}\text{ rad,}\) nous en déduisons que l'angle \(\widehat{OCY}\) mesure : \[ \begin{align*} \widehat{OCY}&=\pi - \widehat{OYC} - \widehat{YOC} \\ &=\pi - \frac{\pi}{2}-\frac{\pi}{4}\\ &=\frac{\pi}{4}\text{ rad}. \end{align*} \] Ainsi, nous avons \(\displaystyle \widehat{OCY}=\widehat{YOC}=\frac{\pi}{4}\text{ rad,}\) donc le triangle OYC est isocèle rectangle en Y, et finalement \(OY=OC\).
Etant donné que \(OY=OC\) et que le repère est orthonormé, cela signifie que l'abscisse et l'ordonnée du point \(C\) sont identiques. Comme \(C\) a pour coordonnées \(\left(\cos \left(\frac{\pi}{4}\right);\sin\left(\frac{\pi}{4}\right)\right),\) on en déduit que : \[ \cos \left(\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}\right). \] En utilisant la Propriété 2 lorsque \(\displaystyle x=\frac{\pi}{4},\) nous avons : \[ \begin{align*} &\cos^{2}\left(\frac{\pi}{4}\right)+\sin^{2}\left(\frac{\pi}{4}\right)=1 \\ \Longleftrightarrow & \cos^{2}\left(\frac{\pi}{4}\right)+\cos^{2}\left(\frac{\pi}{4}\right)=1 \text{ car } \cos \left(\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}\right)\\ \Longleftrightarrow & 2\cos^{2}\left(\frac{\pi}{4}\right)=1 \\ \Longleftrightarrow & \cos^{2}\left(\frac{\pi}{4}\right)=\frac{1}{2} \end{align*} \] Etant donné que le cosinus est positif (compris entre 0 et 1), cette dernière équation admet une unique solution : \[ \begin{align*} \cos\left(\frac{\pi}{4}\right)&=\sqrt{\frac{1}{2}}\\ &=\frac{1}{\sqrt{2}}\\ &=\frac{\sqrt{2}}{\sqrt{2}\times \sqrt{2}}\\ &=\frac{\sqrt{2}}{2}. \end{align*} \] Finalement : \[ \cos\left(\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}. \]
d) Les démonstrations lorsque \(x=\displaystyle \frac{\pi}{6}\) et \(x=\displaystyle \frac{\pi}{3}\) font l'objet de deux exercices corrigés que vous pourrez retrouver dans les feuilles d'exercices d'entraînement (Exercice 1 et 2).
Propriété 4
Pour tout réel \(x\) et tout entier relatif \(k\) :
\[
\begin{align*}
&\cos(x+2k\pi)=\cos(x)\\
&\sin(x+2k\pi)=\sin(x)
\end{align*}
\]
Démonstration
C'est une conséquence directe de la Propriété 1 et de la Définition 2. En effet, à chaque point \(M\) du cercle trigonométrique correspond tous les réels \(x+2k\pi\) avec \(k\) un entier relatif (Propriété 1), et le point \(M\) a pour coordonnées respectivement le cosinus et le sinus de ces nombres réels (Définition 2).
Lorsque \(k=1\), partant du point \(M\), cela signifie que l'on fait un tour complet de cercle dans le sens direct (sens contraire des aiguilles d'une montre) puisque le périmètre du cercle est \(2\pi\). On retombe bien sur le point \(M\).
Plus généralement, partant du point \(M\), lorsque \(k\) est positif, cela signifie que l'on fait \(k\) tours complets de cercle dans le sens direct.
Et lorsque \(k\) est négatif, cela signifie que partant du point \(M\), on fait \(k\) tours complets de cercle dans le sens indirect (sens des aiguilles d'une montre).
C'est une conséquence directe de la Propriété 1 et de la Définition 2. En effet, à chaque point \(M\) du cercle trigonométrique correspond tous les réels \(x+2k\pi\) avec \(k\) un entier relatif (Propriété 1), et le point \(M\) a pour coordonnées respectivement le cosinus et le sinus de ces nombres réels (Définition 2).
Lorsque \(k=1\), partant du point \(M\), cela signifie que l'on fait un tour complet de cercle dans le sens direct (sens contraire des aiguilles d'une montre) puisque le périmètre du cercle est \(2\pi\). On retombe bien sur le point \(M\).
Plus généralement, partant du point \(M\), lorsque \(k\) est positif, cela signifie que l'on fait \(k\) tours complets de cercle dans le sens direct.
Et lorsque \(k\) est négatif, cela signifie que partant du point \(M\), on fait \(k\) tours complets de cercle dans le sens indirect (sens des aiguilles d'une montre).
Propriété 5
Pour tout réel \(x\) :
\[
\cos(x)=\cos(-x).
\]
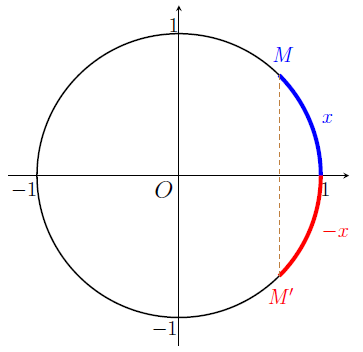
Sur le schéma ci-dessus, nous avons représenté en bleu le point \(M\) associé au réel \(x\), et en rouge le point \(M'\) associé au réel \(-x\).
Nous pouvons voir que le point \(M'\) est le symétrique du point \(M\) par rapport à l'axe des abscisses.
Les points \(M\) et \(M'\) ont donc exactement la même abscisse (mais des ordonnées différentes). Comme l'abscisse du point \(M\) est \(\cos(x)\) (d'après la Définition 2) et celle du point \(M'\) est \(\cos(-x)\), et que ces deux points ont même abscisse, nous avons : \[ \cos(x)=\cos(-x), \] soit la Propriété 5.
Propriété 6
Pour tout réel \(x\) :
\[
\sin(-x)=-\sin(x).
\]
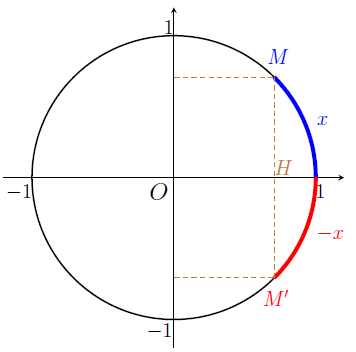
Sur le schéma ci-dessus, nous avons représenté en bleu le point \(M\) associé au réel \(x\), et en rouge le point \(M'\) associé au réel \(-x\).
Nous avons vu précédemment que le point \(M'\) est le symétrique du point \(M\) par rapport à l'axe des abscisses.
Cela signifie que l'ordonnée du point \(M\) est l'opposée de l'ordonnée du point \(M'\). Or d'après la Définition 2, le point \(M\) a pour ordonnée \(\sin(x)\) et le point \(M'\) a pour ordonnée \(\sin(-x)\). Comme l'ordonnée du point \(M'\) est l'opposée de celle du point \(M\), nous avons : \[ \sin(-x)=-\sin(x), \] soit la Propriété 6.
Propriété 7
Pour tout réel \(x\) :
\[
\cos(\pi-x)=-\cos(x).
\]

On se contente ici d'une interprétation géométrique de la Propriété 7.
Sur le graphique ci-dessus, le schéma de gauche, nous avons représenté le point \(M\) associé au réel \(x\) en bleu, et le point \(X\) associé au réel \(\pi\) en orange.
L'angle mesurant \(\pi-x\) radians est représenté sur le schéma de droite en rouge. Il s'agit également de l'angle \(\widehat{MOX}\).
Si nous souhaitons représenter sur le cercle trigonométrique le point associé au réel \(\pi-x\), nous devons "démarrer" à partir du point de coordonnées \((1;0)\).
C'est ce que nous faisons sur le schéma de gauche ci-dessous, où nous avons reporté l'angle mesurant \(x\) radians sur le cercle trigonométrique (en pointillés bleus) et nous avons ainsi le point \(M'\) associé au réel \(\pi-x\) représenté sur le cercle trigonométrique.
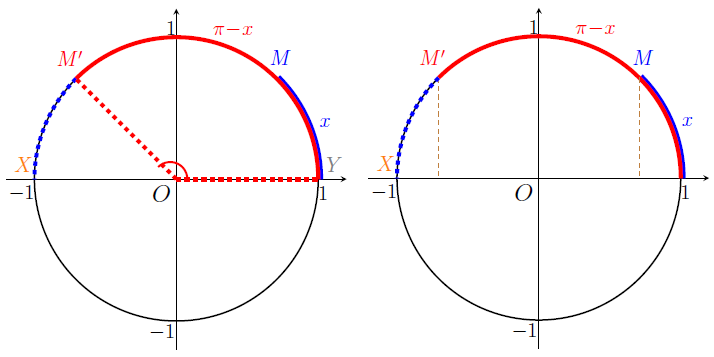
Ainsi l'angle \(\widehat{YOM'}\) a exactement la même mesure que l'angle \(\widehat{MOX}\).
Intéressons-nous aux coordonnées des points \(M\) et \(M'\).
En fait, le point \(M'\) est le symétrique du point \(M\) par rapport à l'axe des ordonnées, ce qui signifie que l'abscisse du point \(M'\) est l'opposée de celle du point \(M\).
D'après la Définition 2, \(M\) a pour abscisse \(\cos(x)\) et \(M'\) a pour abscisse \(\cos(\pi-x)\). Comme les abscisses de ces points sont opposées, nous avons : \[ \cos(\pi-x)=-\cos(x), \] soit la Propriété 7.
Propriété 8
Pour tout réel \(x\) :
\[
\sin(\pi-x)=\sin(x).
\]
Nous repartons de la représentation de l'angle \(\pi-x\) vue dans la Propriété 7, et reproduite ci-dessous.
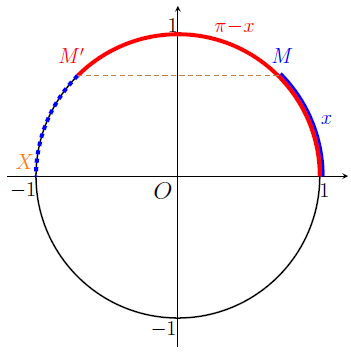
Comme vu précédemment, le point \(M'\) est le symétrique du point \(M\) par rapport à l'axe des ordonnées. Cela signifie donc que l'ordonnée du point \(M'\) est la même que celle du point \(M\).
D'après la Définition 2, \(M\) a pour ordonnée \(\sin(x)\) et \(M'\) a pour ordonnée \(\sin(\pi-x)\). Comme les ordonnées de ces points sont identiques, nous avons : \[ \sin(\pi-x)=\sin(x), \] soit la Propriété 8.

Comme vu précédemment, le point \(M'\) est le symétrique du point \(M\) par rapport à l'axe des ordonnées. Cela signifie donc que l'ordonnée du point \(M'\) est la même que celle du point \(M\).
D'après la Définition 2, \(M\) a pour ordonnée \(\sin(x)\) et \(M'\) a pour ordonnée \(\sin(\pi-x)\). Comme les ordonnées de ces points sont identiques, nous avons : \[ \sin(\pi-x)=\sin(x), \] soit la Propriété 8.
Propriété 9
Pour tout réel \(x\) :
\[
\begin{align*}
&\cos \left(x+\frac{\pi}{2}\right)=-\sin(x)\\
&\sin \left(x+\frac{\pi}{2}\right)=\cos(x).
\end{align*}
\]
L'interprétation géométrique n'étant pas aisée, nous proposons plus loin une démonstration par le calcul.
Même chose pour la Propriété 10.
Même chose pour la Propriété 10.
Propriété 10
Pour tout réel \(x\) :
\[
\begin{align*}
&\cos \left(\frac{\pi}{2}-x\right)=\sin(x)\\
&\sin \left(\frac{\pi}{2}-x\right)=\cos(x).
\end{align*}
\]
D) Formules d'addition et de duplication
Propriété 11
Pour tous réels \(a\) et \(b\) :
\[
\cos (a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)
\]
Démonstration
Attention, dans cette démonstration nous utilisons des résultats sur les vecteurs et les produits scalaires vus en Première.
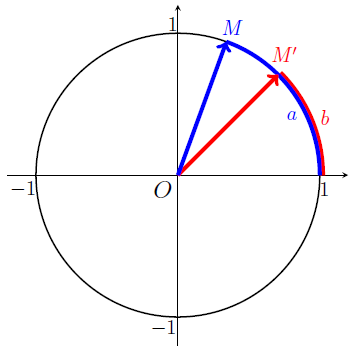
Soit \(M\) le point du cercle trigonométrique associé au réel \(a\), et \(M'\) le point du cercle trigonométrique associé au réel \(b\).
Comme \(M\) a pour coordonnées \((\cos (a), \sin (a))\) d'après la Définition 2, et \(O\) a pour coordonnées \((0,0)\), alors le vecteur \(\vec{OM}\) a pour coordonnées : \[ \begin{align*} \vec{OM}&=\left( \begin{matrix} x_{M}-x_{O} \\ y_{M}-y_{O} \end{matrix} \right)\\ &=\left( \begin{matrix} \cos(a)-0 \\ \sin(a)-0 \end{matrix} \right)\\ &=\left( \begin{matrix} \cos(a) \\ \sin(a) \end{matrix} \right) \end{align*} \] De même avec le point \(M'\), nous avons : \[ \vec{OM'}=\left( \begin{matrix} \cos(b) \\ \sin(b) \end{matrix} \right) \] Nous avons d'une part : \[ \vec{OM}.\vec{OM'}=\cos(a)\cos(b)+\sin(a)\sin(b), \] et d'autre part : \[ \begin{align*} \vec{OM}.\vec{OM'}&=\left \|\vec{OM} \right \| \left \|\vec{OM'} \right\| \cos\left(\vec{OM},\vec{OM'}\right)\\ &=1\times 1 \times \cos\left(\vec{OM},\vec{OM'}\right) \\ &=\cos\left(\vec{OM},\vec{OM'}\right) \\ &=\cos(a-b). \end{align*} \] Par conséquent pour tous réels \(a\) et \(b\) nous avons : \[ \cos (a-b)=\cos(a)\cos(b)+\sin(a)\sin(b), \] soit la Propriété 11.
Attention, dans cette démonstration nous utilisons des résultats sur les vecteurs et les produits scalaires vus en Première.

Soit \(M\) le point du cercle trigonométrique associé au réel \(a\), et \(M'\) le point du cercle trigonométrique associé au réel \(b\).
Comme \(M\) a pour coordonnées \((\cos (a), \sin (a))\) d'après la Définition 2, et \(O\) a pour coordonnées \((0,0)\), alors le vecteur \(\vec{OM}\) a pour coordonnées : \[ \begin{align*} \vec{OM}&=\left( \begin{matrix} x_{M}-x_{O} \\ y_{M}-y_{O} \end{matrix} \right)\\ &=\left( \begin{matrix} \cos(a)-0 \\ \sin(a)-0 \end{matrix} \right)\\ &=\left( \begin{matrix} \cos(a) \\ \sin(a) \end{matrix} \right) \end{align*} \] De même avec le point \(M'\), nous avons : \[ \vec{OM'}=\left( \begin{matrix} \cos(b) \\ \sin(b) \end{matrix} \right) \] Nous avons d'une part : \[ \vec{OM}.\vec{OM'}=\cos(a)\cos(b)+\sin(a)\sin(b), \] et d'autre part : \[ \begin{align*} \vec{OM}.\vec{OM'}&=\left \|\vec{OM} \right \| \left \|\vec{OM'} \right\| \cos\left(\vec{OM},\vec{OM'}\right)\\ &=1\times 1 \times \cos\left(\vec{OM},\vec{OM'}\right) \\ &=\cos\left(\vec{OM},\vec{OM'}\right) \\ &=\cos(a-b). \end{align*} \] Par conséquent pour tous réels \(a\) et \(b\) nous avons : \[ \cos (a-b)=\cos(a)\cos(b)+\sin(a)\sin(b), \] soit la Propriété 11.
A partir de la Propriété 11, nous pouvons déduire une formule pour \(\cos(a+b)\).
Propriété 12
Pour tous réels \(a\) et \(b\) :
\[
\cos (a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)
\]
Démonstration
\[ \begin{align*} \cos (a+b)&=\cos \left(a-(-b)\right)\\ &=\cos(a)\cos(-b)+\sin(a)\sin(-b) \\ &=\cos(a)\cos(b)+\sin(a)\times \left(-\sin(b)\right) \\ &=\cos(a)\cos(b)-\sin(a)\sin(b) \end{align*} \] Le passage de la première à la deuxième ligne s'obtient en utilisant la Propriété 11.
Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 5 \(\left(\cos(-b)=\cos(b)\right)\) et la Propriété 6 \(\left(\sin(-b)=-\sin(b)\right)\).
\[ \begin{align*} \cos (a+b)&=\cos \left(a-(-b)\right)\\ &=\cos(a)\cos(-b)+\sin(a)\sin(-b) \\ &=\cos(a)\cos(b)+\sin(a)\times \left(-\sin(b)\right) \\ &=\cos(a)\cos(b)-\sin(a)\sin(b) \end{align*} \] Le passage de la première à la deuxième ligne s'obtient en utilisant la Propriété 11.
Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 5 \(\left(\cos(-b)=\cos(b)\right)\) et la Propriété 6 \(\left(\sin(-b)=-\sin(b)\right)\).
Dans ce qui suit, nous démontrons la première partie des Propriétés 9 et 10 à partir des Propriétés 11 et 12.
Ces démonstrations nécessitent de connaître les valeurs remarquables du sinus et du cosinus rappelées dans le tableau sous la Propriété 3.
Démonstrations
Démonstration de la première partie de la Propriété 9 : \[ \begin{align*} \cos \left(x+\frac{\pi}{2}\right)&=\cos(x)\cos\left(\frac{\pi}{2}\right)-\sin(x)\sin\left(\frac{\pi}{2}\right)\\ &=\cos(x)\times 0-\sin(x)\times 1\\ &=0-\sin(x)\\ &=-\sin(x) \end{align*} \]
Démonstration de la première partie de la Propriété 10 : \[ \begin{align*} \cos \left(\frac{\pi}{2}-x\right)&=\cos\left(\frac{\pi}{2}\right)\cos(x)+\sin\left(\frac{\pi}{2}\right)\sin(x)\\ &=0\times \cos(x)+1\times \sin(x)\\ &=0+\sin(x)\\ &=\sin(x) \end{align*} \]
Démonstration de la première partie de la Propriété 9 : \[ \begin{align*} \cos \left(x+\frac{\pi}{2}\right)&=\cos(x)\cos\left(\frac{\pi}{2}\right)-\sin(x)\sin\left(\frac{\pi}{2}\right)\\ &=\cos(x)\times 0-\sin(x)\times 1\\ &=0-\sin(x)\\ &=-\sin(x) \end{align*} \]
Démonstration de la première partie de la Propriété 10 : \[ \begin{align*} \cos \left(\frac{\pi}{2}-x\right)&=\cos\left(\frac{\pi}{2}\right)\cos(x)+\sin\left(\frac{\pi}{2}\right)\sin(x)\\ &=0\times \cos(x)+1\times \sin(x)\\ &=0+\sin(x)\\ &=\sin(x) \end{align*} \]
Propriété 13
Pour tous réels \(a\) et \(b\) :
\[
\sin (a-b)=\sin(a)\cos(b)-\cos(a)\sin(b)
\]
Démonstration
\[ \begin{align*} \sin \left(a-b\right)&=\cos\left(\frac{\pi}{2}-(a-b)\right) \text{ (d'après la Propriété 10)}\\ &=\cos\left(\left(\frac{\pi}{2}-a\right)+b\right) \\ &=\cos\left(\frac{\pi}{2}-a\right)\cos(b)-\sin\left(\frac{\pi}{2}-a\right)\sin(b) \\ &=\sin(a)\cos(b)-\cos(a)\sin(b). \end{align*} \] Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 12.
Le passage de la troisième à la quatrième ligne s'obtient en utilisant la Propriété 10.
\[ \begin{align*} \sin \left(a-b\right)&=\cos\left(\frac{\pi}{2}-(a-b)\right) \text{ (d'après la Propriété 10)}\\ &=\cos\left(\left(\frac{\pi}{2}-a\right)+b\right) \\ &=\cos\left(\frac{\pi}{2}-a\right)\cos(b)-\sin\left(\frac{\pi}{2}-a\right)\sin(b) \\ &=\sin(a)\cos(b)-\cos(a)\sin(b). \end{align*} \] Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 12.
Le passage de la troisième à la quatrième ligne s'obtient en utilisant la Propriété 10.
A partir de la Propriété 13, nous pouvons déduire une formule pour \(\sin(a+b)\).
Propriété 14
Pour tous réels \(a\) et \(b\) :
\[
\sin (a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)
\]
Démonstration
\[ \begin{align*} \sin (a+b)&=\sin \left(a-(-b)\right)\\ &=\sin(a)\cos(-b)-\cos(a)\sin(-b) \\ &=\sin(a)\cos(b)-\cos(a)\times \left(-\sin(b)\right) \\ &=\sin(a)\cos(b)+\cos(a)\sin(b) \end{align*} \] Le passage de la première à la deuxième ligne s'obtient en utilisant la Propriété 13.
Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 5 \(\left(\cos(-b)=\cos(b)\right)\) et la Propriété 6 \(\left(\sin(-b)=-\sin(b)\right)\).
\[ \begin{align*} \sin (a+b)&=\sin \left(a-(-b)\right)\\ &=\sin(a)\cos(-b)-\cos(a)\sin(-b) \\ &=\sin(a)\cos(b)-\cos(a)\times \left(-\sin(b)\right) \\ &=\sin(a)\cos(b)+\cos(a)\sin(b) \end{align*} \] Le passage de la première à la deuxième ligne s'obtient en utilisant la Propriété 13.
Le passage de la deuxième à la troisième ligne s'obtient en utilisant la Propriété 5 \(\left(\cos(-b)=\cos(b)\right)\) et la Propriété 6 \(\left(\sin(-b)=-\sin(b)\right)\).
Dé même que précédemment, nous pouvons démontrer la deuxième partie des Propriétés 9 et 10 à partir des Propriétés 13 et 14. Nous avons besoin à nouveau d'utiliser les valeurs remarquables du sinus et du cosinus rappelées dans le tableau sous la Propriété 3.
Démonstrations
Démonstration de la deuxième partie de la Propriété 9 : \[ \begin{align*} \sin \left(x+\frac{\pi}{2}\right)&=\sin(x)\cos\left(\frac{\pi}{2}\right)+\cos(x)\sin\left(\frac{\pi}{2}\right)\\ &=\sin(x)\times 0+\cos(x)\times 1\\ &=0+\cos(x)\\ &=\cos(x) \end{align*} \]
Démonstration de la deuxième partie de la Propriété 10 : \[ \begin{align*} \sin \left(\frac{\pi}{2}-x\right)&=\sin\left(\frac{\pi}{2}\right)\cos(x)-\cos\left(\frac{\pi}{2}\right)\sin(x)\\ &=1\times \cos(x)-0\times \sin(x)\\ &=\cos(x)-0\\ &=\cos(x) \end{align*} \]
Démonstration de la deuxième partie de la Propriété 9 : \[ \begin{align*} \sin \left(x+\frac{\pi}{2}\right)&=\sin(x)\cos\left(\frac{\pi}{2}\right)+\cos(x)\sin\left(\frac{\pi}{2}\right)\\ &=\sin(x)\times 0+\cos(x)\times 1\\ &=0+\cos(x)\\ &=\cos(x) \end{align*} \]
Démonstration de la deuxième partie de la Propriété 10 : \[ \begin{align*} \sin \left(\frac{\pi}{2}-x\right)&=\sin\left(\frac{\pi}{2}\right)\cos(x)-\cos\left(\frac{\pi}{2}\right)\sin(x)\\ &=1\times \cos(x)-0\times \sin(x)\\ &=\cos(x)-0\\ &=\cos(x) \end{align*} \]
Propriété 15
Pour tout réel \(a\) :
\[
\begin{align*}
\cos (2a)&=\cos^{2}(a)-\sin^{2}(a) \\
\cos (2a)&=2\cos^{2}(a)-1\\
\cos (2a)&=1-2\sin^{2}(a)
\end{align*}
\]
Démonstrations
La première équation provient de l'application directe de la Propriété 12. En effet : \[ \begin{align*} \cos(2a)&=\cos(a+a) \\ &=\cos(a)\cos(a)-\sin(a)\sin(a)\\ &=\cos^{2}(a)-\sin^{2}(a). \end{align*} \]
La deuxième équation s'obtient à partir de la première et en utilisant la Propriété 2. En effet nous venons juste de démontrer que : \[ \cos(2a)=\cos^{2}(a)-\sin^{2}(a). \] Or d'après la Propriété 2, nous avons : \[ \begin{align*} & \cos^{2}(a)+\sin^{2}(a)=1 \\ \Longleftrightarrow & \sin^{2}(a)=1-\cos^{2}(a). \end{align*} \] En remplaçant \(\sin^{2}(a)\) par cette expression dans le calcul de \(\cos(2a)\), nous obtenons : \[ \begin{align*} \cos(2a)&=\cos^{2}(a)-\sin^{2}(a)\\ &=\cos^{2}(a)-\left(1-\cos^{2}(a)\right)\\ &=\cos^{2}(a)-1+\cos^{2}(a)\\ &=2\cos^{2}(a)-1, \end{align*} \] soit la deuxième équation.
Pour la troisième équation, on part à nouveau de la première équation et de la Propriété 2, sauf que partant de cette dernière, nous isolons \(\cos^{2}(a)\) : \[ \begin{align*} & \cos^{2}(a)+\sin^{2}(a)=1 \\ \Longleftrightarrow & \cos^{2}(a)=1-\sin^{2}(a), \end{align*} \] que nous remplaçons dans la première équation : \[ \begin{align*} \cos(2a)&=\cos^{2}(a)-\sin^{2}(a)\\ &=\left(1-\sin^{2}(a)\right)-\sin^{2}(a)\\ &=1-\sin^{2}(a)-\sin^{2}(a)\\ &=1-2\sin^{2}(a), \end{align*} \] soit la troisième équation.
La première équation provient de l'application directe de la Propriété 12. En effet : \[ \begin{align*} \cos(2a)&=\cos(a+a) \\ &=\cos(a)\cos(a)-\sin(a)\sin(a)\\ &=\cos^{2}(a)-\sin^{2}(a). \end{align*} \]
La deuxième équation s'obtient à partir de la première et en utilisant la Propriété 2. En effet nous venons juste de démontrer que : \[ \cos(2a)=\cos^{2}(a)-\sin^{2}(a). \] Or d'après la Propriété 2, nous avons : \[ \begin{align*} & \cos^{2}(a)+\sin^{2}(a)=1 \\ \Longleftrightarrow & \sin^{2}(a)=1-\cos^{2}(a). \end{align*} \] En remplaçant \(\sin^{2}(a)\) par cette expression dans le calcul de \(\cos(2a)\), nous obtenons : \[ \begin{align*} \cos(2a)&=\cos^{2}(a)-\sin^{2}(a)\\ &=\cos^{2}(a)-\left(1-\cos^{2}(a)\right)\\ &=\cos^{2}(a)-1+\cos^{2}(a)\\ &=2\cos^{2}(a)-1, \end{align*} \] soit la deuxième équation.
Pour la troisième équation, on part à nouveau de la première équation et de la Propriété 2, sauf que partant de cette dernière, nous isolons \(\cos^{2}(a)\) : \[ \begin{align*} & \cos^{2}(a)+\sin^{2}(a)=1 \\ \Longleftrightarrow & \cos^{2}(a)=1-\sin^{2}(a), \end{align*} \] que nous remplaçons dans la première équation : \[ \begin{align*} \cos(2a)&=\cos^{2}(a)-\sin^{2}(a)\\ &=\left(1-\sin^{2}(a)\right)-\sin^{2}(a)\\ &=1-\sin^{2}(a)-\sin^{2}(a)\\ &=1-2\sin^{2}(a), \end{align*} \] soit la troisième équation.
Propriété 16
Pour tout réel \(a\) :
\[
\sin(2a)=2\sin(a)\cos(a)
\]
Démonstration
Nous utilisons simplement la Propriété 14 : \[ \begin{align*} \sin(2a)&=\sin(a+a)\\ &=\sin(a)\cos(a)+\cos(a)\sin(a)\\ &=\sin(a)\cos(a)+\sin(a)\cos(a)\\ &=2\sin(a)\cos(a), \end{align*} \] soit la Propriété 16.
Nous utilisons simplement la Propriété 14 : \[ \begin{align*} \sin(2a)&=\sin(a+a)\\ &=\sin(a)\cos(a)+\cos(a)\sin(a)\\ &=\sin(a)\cos(a)+\sin(a)\cos(a)\\ &=2\sin(a)\cos(a), \end{align*} \] soit la Propriété 16.
E) Equations trigonométriques
Théorème 1
Pour tout réel \(a\), l'ensemble des solutions de l'équation \(\cos(x)=\cos(a)\) est l'ensemble des réels \(x\) qui peuvent s'écrire \(x=a+2k\pi\) ou \(x=-a+2k'\pi\), avec \(k\in \mathbb{Z}\) et \(k'\in \mathbb{Z}\).
Quelques explications : une première solution assez évidente de l'équation \(\cos(x)=\cos(a)\) est \(x=a\).
Mais ce n'est pas la seule. D'après la Propriété 4, nous avons pour tout \(k\in \mathbb{Z}\) : \[ \cos(a)=\cos(a+2k\pi) \] Donc l'ensemble des réels s'écrivant \(x=a+2k\pi\) avec \(k\in \mathbb{Z}\) sont solutions de l'équation \(\cos(x)=\cos(a)\).
D'autre part, d'après la Propriété 5, nous avons \(\cos(a)=\cos(-a)\) et par suite, \(\cos(a)=\cos(-a+2k\pi)\) avec \(k\in \mathbb{Z}\) d'après la Propriété 4.
Donc l'ensemble des réels s'écrivant \(x=-a+2k'\pi\) avec \(k'\in \mathbb{Z}\) sont aussi solutions de l'équation \(\cos(x)=\cos(a)\).
Mais ce n'est pas la seule. D'après la Propriété 4, nous avons pour tout \(k\in \mathbb{Z}\) : \[ \cos(a)=\cos(a+2k\pi) \] Donc l'ensemble des réels s'écrivant \(x=a+2k\pi\) avec \(k\in \mathbb{Z}\) sont solutions de l'équation \(\cos(x)=\cos(a)\).
D'autre part, d'après la Propriété 5, nous avons \(\cos(a)=\cos(-a)\) et par suite, \(\cos(a)=\cos(-a+2k\pi)\) avec \(k\in \mathbb{Z}\) d'après la Propriété 4.
Donc l'ensemble des réels s'écrivant \(x=-a+2k'\pi\) avec \(k'\in \mathbb{Z}\) sont aussi solutions de l'équation \(\cos(x)=\cos(a)\).
Théorème 2
Pour tout réel \(a\), l'ensemble des solutions de l'équation \(\sin(x)=\sin(a)\) est l'ensemble des réels \(x\) qui peuvent s'écrire \(x=a+2k\pi\) ou \(x=\pi-a+2k'\pi\), avec \(k\in \mathbb{Z}\) et \(k'\in \mathbb{Z}\).
Le raisonnement est assez proche de celui du théorème précédent. Une première solution assez évidente de l'équation \(\sin(x)=\sin(a)\) est \(x=a\).
Ce n'est pas la seule, puisque d'après la Propriété 4, nous avons pour tout \(k\in \mathbb{Z}\) : \[ \sin(a)=\sin(a+2k\pi) \] Donc l'ensemble des réels s'écrivant \(x=a+2k\pi\) avec \(k\in \mathbb{Z}\) sont solutions de l'équation \(\sin(x)=\sin(a)\).
D'autre part, d'après la Propriété 8, nous avons \(\sin(a)=\sin(\pi-a)\) et par suite, \(\sin(a)=\sin(\pi-a+2k'\pi)\) avec \(k'\in \mathbb{Z}\) d'après la Propriété 4.
Donc l'ensemble des réels s'écrivant \(x=\pi-a+2k'\pi\) avec \(k'\in \mathbb{Z}\) sont aussi solutions de l'équation \(\sin(x)=\sin(a)\).
Ce n'est pas la seule, puisque d'après la Propriété 4, nous avons pour tout \(k\in \mathbb{Z}\) : \[ \sin(a)=\sin(a+2k\pi) \] Donc l'ensemble des réels s'écrivant \(x=a+2k\pi\) avec \(k\in \mathbb{Z}\) sont solutions de l'équation \(\sin(x)=\sin(a)\).
D'autre part, d'après la Propriété 8, nous avons \(\sin(a)=\sin(\pi-a)\) et par suite, \(\sin(a)=\sin(\pi-a+2k'\pi)\) avec \(k'\in \mathbb{Z}\) d'après la Propriété 4.
Donc l'ensemble des réels s'écrivant \(x=\pi-a+2k'\pi\) avec \(k'\in \mathbb{Z}\) sont aussi solutions de l'équation \(\sin(x)=\sin(a)\).
II) Fonctions sinus et cosinus
A) Fonction sinus
Théorème 3
La fonction sinus est périodique de période \(2\pi\). On dit également que la fonction sinus est \(2\pi\)-périodique.
Ceci provient directement de la Propriété 4 étant donné que pour tout réel \(x\), nous avons \(\sin(x+2\pi)=\sin(x)\).
Théorème 4
La fonction sinus est impaire.
Ceci provient directement de la Propriété 6 étant donné que pour tout réel \(x\), nous avons \(\sin(-x)=-\sin(x)\).
Théorème 5
\[
\lim_{x\rightarrow 0}\frac{\sin(x)}{x}=1.
\]
La limite suivante est nécessaire au calcul de la dérivée de la fonction sinus, c'est pourquoi nous la voyons dès à présent.
Théorème 6
\[
\lim_{x\rightarrow 0}\frac{\cos(x)-1}{x}=0.
\]
Démonstration :
Lorsque \(x\) est proche de 0 : \[ \begin{align*} \frac{\cos(x)-1}{x}&=\frac{(\cos(x)-1) \color{red}( \color{red} \cos \color{red} ( \color{red} x \color{red} ) \color{red} + \color{red} 1 \color{red})}{x \color{red}( \color{red} \cos \color{red} ( \color{red} x \color{red} ) \color{red} + \color{red} 1 \color{red})}\\ &=\frac{\cos^{2}(x)-1}{x(\cos(x)+1)}\\ &=\frac{-\sin^{2}(x)}{x(\cos(x)+1)}\text{ (d'après la Propriété 2)}\\ &=-\frac{\sin(x)}{\cos(x)+1} \times \frac{\sin(x)}{x} \end{align*} \] Etant donné que \(\lim_{x\rightarrow 0} \sin(x)=0\) et \(\lim_{x\rightarrow 0} \cos(x)=1\), nous en déduisons que \(\displaystyle \lim_{x\rightarrow 0} \frac{\sin(x)}{\cos(x)+1}=\frac{0}{1+1}=0\).
D'autre part, d'après le Théorème 5, nous avons \(\displaystyle \lim_{x\rightarrow 0} \frac{\sin(x)}{x}=1\).
En conclusion, nous avons \(\displaystyle \lim_{x\rightarrow 0} -\frac{\sin(x)}{\cos(x)+1} \times \frac{\sin(x)}{x}=0\), donc \(\displaystyle \lim_{x\rightarrow 0}\frac{\cos(x)-1}{x}=0\), soit le Théorème 6.
Lorsque \(x\) est proche de 0 : \[ \begin{align*} \frac{\cos(x)-1}{x}&=\frac{(\cos(x)-1) \color{red}( \color{red} \cos \color{red} ( \color{red} x \color{red} ) \color{red} + \color{red} 1 \color{red})}{x \color{red}( \color{red} \cos \color{red} ( \color{red} x \color{red} ) \color{red} + \color{red} 1 \color{red})}\\ &=\frac{\cos^{2}(x)-1}{x(\cos(x)+1)}\\ &=\frac{-\sin^{2}(x)}{x(\cos(x)+1)}\text{ (d'après la Propriété 2)}\\ &=-\frac{\sin(x)}{\cos(x)+1} \times \frac{\sin(x)}{x} \end{align*} \] Etant donné que \(\lim_{x\rightarrow 0} \sin(x)=0\) et \(\lim_{x\rightarrow 0} \cos(x)=1\), nous en déduisons que \(\displaystyle \lim_{x\rightarrow 0} \frac{\sin(x)}{\cos(x)+1}=\frac{0}{1+1}=0\).
D'autre part, d'après le Théorème 5, nous avons \(\displaystyle \lim_{x\rightarrow 0} \frac{\sin(x)}{x}=1\).
En conclusion, nous avons \(\displaystyle \lim_{x\rightarrow 0} -\frac{\sin(x)}{\cos(x)+1} \times \frac{\sin(x)}{x}=0\), donc \(\displaystyle \lim_{x\rightarrow 0}\frac{\cos(x)-1}{x}=0\), soit le Théorème 6.
Nous avons à présent l'ensemble des éléments pour déterminer la dérivée de la fonction sinus.
Théorème 7
La fonction sinus est dérivable sur \(\mathbb{R}\), et pour tout réel \(x\) nous avons :
\[
\sin'(x)=\cos(x).
\]
Démonstration :
Calculons préalablement \(\displaystyle \frac{\sin(x+h)-\sin(x)}{h}\) en utilisant la Propriété 14.
\[ \begin{align*} \frac{\sin(x+h)-\sin(x)}{h}&=\frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h}\\ &=\frac{\sin(x)(\cos(h)-1)+\sin(h)\cos(x)}{h}\\ &=\sin(x)\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h} \end{align*} \] D'après le Théorème 6, nous avons : \[ \lim_{h\rightarrow 0}\frac{\cos(h)-1}{h}=0, \] et d'après le Théorème 5, nous avons : \[ \lim_{h\rightarrow 0}\frac{\sin(h)}{h}=1. \] Nous déduisons par conséquent que \[ \lim_{h\rightarrow 0} \frac{\sin(x+h)-\sin(x)}{h}=\cos(x). \] Or ce qui est à gauche de cette égalité est précisément \(\sin'(x)\) (voir le chapitre sur les dérivées).
On en déduit ainsi que : \[ \sin'(x)=\cos(x), \] c'est-à-dire le Théorème 7.
Calculons préalablement \(\displaystyle \frac{\sin(x+h)-\sin(x)}{h}\) en utilisant la Propriété 14.
\[ \begin{align*} \frac{\sin(x+h)-\sin(x)}{h}&=\frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h}\\ &=\frac{\sin(x)(\cos(h)-1)+\sin(h)\cos(x)}{h}\\ &=\sin(x)\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h} \end{align*} \] D'après le Théorème 6, nous avons : \[ \lim_{h\rightarrow 0}\frac{\cos(h)-1}{h}=0, \] et d'après le Théorème 5, nous avons : \[ \lim_{h\rightarrow 0}\frac{\sin(h)}{h}=1. \] Nous déduisons par conséquent que \[ \lim_{h\rightarrow 0} \frac{\sin(x+h)-\sin(x)}{h}=\cos(x). \] Or ce qui est à gauche de cette égalité est précisément \(\sin'(x)\) (voir le chapitre sur les dérivées).
On en déduit ainsi que : \[ \sin'(x)=\cos(x), \] c'est-à-dire le Théorème 7.
Théorème 8
Soit \(u\) une fonction dérivable sur un intervalle \(I\). Alors la fonction \(x\rightarrow \sin \left(u(x)\right)\) est dérivable sur \(I\) et nous avons :
\[
\sin'\left(u(x)\right)=u'(x)\cos \left(u(x)\right).
\]
Démonstration :
Il s'agit d'une application immédiate du théorème de dérivation d'une fonction composée. Avec \(v(x)=\sin(x)\), nous avons \((v \circ u)(x)=\sin \left(u(x)\right)\), et nous souhaitons calculer \[ \left(v\circ u\right)'(x)=v'\left(u(x)\right)\times u'(x) \] Or \(v'(x)=\cos(x)\) d'après le Théorème 7. En remplaçant, nous obtenons : \[ \begin{align*} \sin'\left(u(x)\right)=&\cos\left(u(x)\right)\times u'(x)\\ &=u'(x)\cos \left(u(x)\right), \end{align*} \] c'est-à-dire le Théorème 8.
Il s'agit d'une application immédiate du théorème de dérivation d'une fonction composée. Avec \(v(x)=\sin(x)\), nous avons \((v \circ u)(x)=\sin \left(u(x)\right)\), et nous souhaitons calculer \[ \left(v\circ u\right)'(x)=v'\left(u(x)\right)\times u'(x) \] Or \(v'(x)=\cos(x)\) d'après le Théorème 7. En remplaçant, nous obtenons : \[ \begin{align*} \sin'\left(u(x)\right)=&\cos\left(u(x)\right)\times u'(x)\\ &=u'(x)\cos \left(u(x)\right), \end{align*} \] c'est-à-dire le Théorème 8.
Dans ce qui suit, nous proposons d'étudier la fonction \(\sin(x)\) sur l'intervalle \([-\pi;\pi]\).
Soit \(f\) la fonction définie pour tout réel \(x\in [-\pi;\pi]\) par \(f(x)=\sin(x)\).
Nous savons que d'après le Théorème 4, la fonction sinus est impaire. Par conséquent, nous pouvons limiter dans un premier temps l'étude de la fonction \(f\) sur l'intervalle \([0;\pi]\).
Nous savons d'après le Théorème 7 que \(f'(x)=\cos(x)\). Etant donné que \(\cos(x)\) est positif pour tout \(\displaystyle x\in \left[0;\frac{\pi}{2}\right]\) et négatif pour tout \(\displaystyle x\in \left[\frac{\pi}{2};\pi\right]\), nous pouvons en déduire que la fonction \(f\) est croissante sur \(\displaystyle \left[0;\frac{\pi}{2}\right]\) et décroissante sur \(\displaystyle \left[\frac{\pi}{2};\pi\right]\).
Par conséquent, elle admet un maximum en \(\displaystyle \frac{\pi}{2}\) qui vaut \(\displaystyle f \left(\frac{\pi}{2}\right)=\sin \left(\frac{\pi}{2}\right)=1\). Nous savons également que \(f(0)=\sin(0)=0\) et \(f(\pi)=\sin(\pi)=0\)
Nous pouvons à présent dresser le tableau de variations de la fonction sinus sur l'intervalle \([0;\pi]\) :
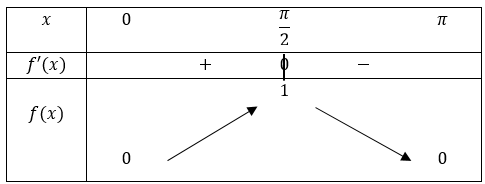
Etant donné que la fonction sinus est impaire, nous en déduisons immédiatement le tableau de variations sur l'intervalle \([-\pi;0]\) :

Et finalement sur l'intervalle \([-\pi;\pi]\) :

Nous pouvons également calculer l'équation de la tangente en 0 à la courbe représentative de la fonction sinus : \[ \begin{align*} y&=f'(0)(x-0)+f(0)\\ &=\cos(0)(x-0)+\sin(0)\\ &=1(x-0)\\ &=x \end{align*} \] Sur le graphique suivant figure la courbe représentative de la fonction sinus sur \([-\pi;\pi]\) ainsi que la tangente à cette courbe (notée \(\mathcal{T}\)) en 0 :
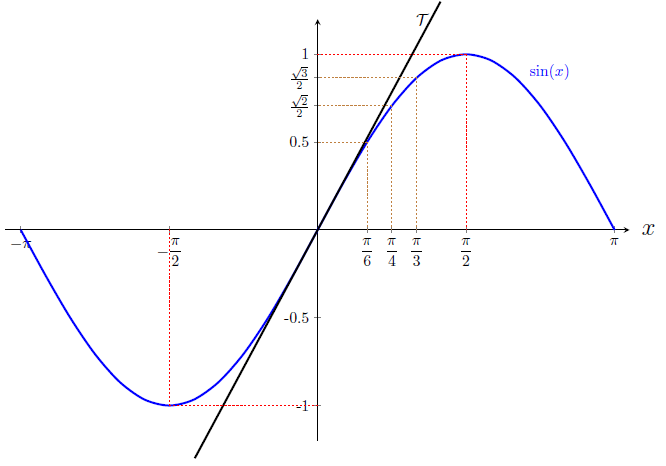
B) Fonction cosinus
Théorème 9
La fonction cosinus est périodique de période \(2\pi\). On dit également que la fonction cosinus est \(2\pi\)-périodique.
Ceci provient directement de la Propriété 4 étant donné que pour tout réel \(x\), nous avons \(\cos(x+2\pi)=\cos(x)\).
Théorème 10
La fonction cosinus est paire.
Ceci provient directement de la Propriété 5 étant donné que pour tout réel \(x\), nous avons \(\cos(-x)=\cos(x)\).
Théorème 11
La fonction cosinus est dérivable sur \(\mathbb{R}\), et pour tout réel \(x\) nous avons :
\[
\cos'(x)=-\sin(x).
\]
Démonstration :
D'après la Propriété 10, nous avons
\[
\displaystyle \cos(x)=\sin\left(\frac{\pi}{2}-x\right).
\]
En utilisant le Théorème 8, nous obtenons la dérivée de \(\cos(x)\) :
\[
\begin{align*}
\cos'(x)&=\left(\frac{\pi}{2}-x\right)'\cos \left(\frac{\pi}{2}-x\right)\\
&=-\cos \left(\frac{\pi}{2}-x\right)\\
&=-\sin(x),
\end{align*}
\]
d'après la Propriété 10, soit le résultat énoncé dans le Théorème 11.
Remarque : nous aurions pu aussi utiliser la Propriété 9 pour effectuer cette même démonstration.
Remarque : nous aurions pu aussi utiliser la Propriété 9 pour effectuer cette même démonstration.
Théorème 12
Soit \(u\) une fonction dérivable sur un intervalle \(I\). Alors la fonction \(x\rightarrow \cos \left(u(x)\right)\) est dérivable sur \(I\) et nous avons :
\[
\cos'\left(u(x)\right)=-u'(x)\sin \left(u(x)\right).
\]
Démonstration :
Il s'agit d'une application immédiate du théorème de dérivation d'une fonction composée. Avec \(v(x)=\cos(x)\), nous avons \((v \circ u)(x)=\cos \left(u(x)\right)\), et nous souhaitons calculer \[ \left(v\circ u\right)'(x)=v'\left(u(x)\right)\times u'(x) \] Or \(v'(x)=-\sin(x)\) d'après le Théorème 11. En remplaçant, nous obtenons : \[ \begin{align*} \cos'\left(u(x)\right)=&-\sin\left(u(x)\right)\times u'(x)\\ &=-u'(x)\sin \left(u(x)\right), \end{align*} \] c'est-à-dire le Théorème 12.
Il s'agit d'une application immédiate du théorème de dérivation d'une fonction composée. Avec \(v(x)=\cos(x)\), nous avons \((v \circ u)(x)=\cos \left(u(x)\right)\), et nous souhaitons calculer \[ \left(v\circ u\right)'(x)=v'\left(u(x)\right)\times u'(x) \] Or \(v'(x)=-\sin(x)\) d'après le Théorème 11. En remplaçant, nous obtenons : \[ \begin{align*} \cos'\left(u(x)\right)=&-\sin\left(u(x)\right)\times u'(x)\\ &=-u'(x)\sin \left(u(x)\right), \end{align*} \] c'est-à-dire le Théorème 12.
Soit \(g\) la fonction définie pour tout réel \(x\in [-\pi;\pi]\) par \(g(x)=\cos(x)\).
Nous savons que d'après le Théorème 10, la fonction cosinus est paire. Par conséquent, nous pouvons limiter dans un premier temps l'étude de la fonction \(g\) sur l'intervalle \([0;\pi]\).
Nous savons d'après le Théorème 11 que \(g'(x)=-\sin(x)\). Etant donné que \(\sin(x)\) est positif pour tout \(x\in [0;\pi]\), nous pouvons en déduire que \(-\sin(x)\) est négatif pour tout \(x\in [0;\pi]\) et par conséquent que la fonction \(g\) est décroissante sur \([0;\pi]\).
Nous savons que \(g(0)=\cos(0)=1\) et \(g(\pi)=\cos(\pi)=-1\)
Nous pouvons à présent dresser le tableau de variations de la fonction cosinus sur l'intervalle \([0;\pi]\) :
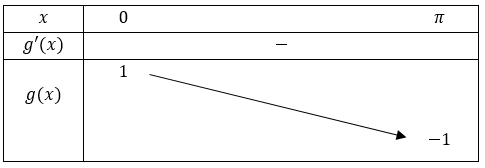
Etant donné que la fonction cosinus est paire, nous en déduisons immédiatement le tableau de variations sur l'intervalle \([-\pi;0]\) :
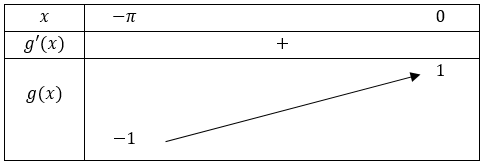
Et finalement sur l'intervalle \([-\pi;\pi]\) :

Nous pouvons également calculer l'équation de la tangente en 0 à la courbe représentative de la fonction cosinus : \[ \begin{align*} y&=f'(0)(x-0)+f(0)\\ &=-\sin(0)(x-0)+\cos(0)\\ &=0(x-0)+1\\ &=1 \end{align*} \] Sur le graphique suivant figure la courbe représentative de la fonction cosinus sur \([-\pi;\pi]\) ainsi que la tangente à cette courbe (notée \(\mathcal{T}\)) en 0 :
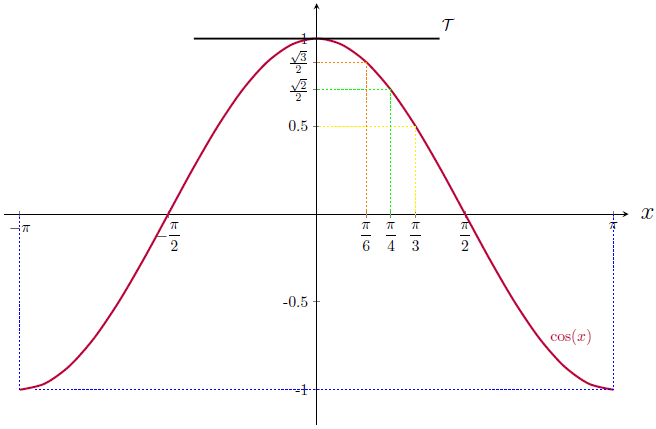
C) Primitives des fonctions trigonométriques
Théorème 13
Les primitives de la fonction \(x\rightarrow \sin(x)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow -\cos(x)+k\) avec \(k\in \mathbb{R}\).
Démonstration :
Soit \(k\) un réel et \(F\) la fonction définie pour tout réel \(x\) par \(F(x)=-\cos(x)\).
\(F\) est dérivable sur \(\mathbb{R}\) et pour tout réel \(x\), nous avons : \[ F'(x)=-\left(-\sin(x)\right)=\sin(x) \] après utilisation du Théorème 11.
Donc \(F\) est une primitive de la fonction sinus sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction sinus sont les fonctions de la forme \(x\rightarrow -\cos(x)+k\) avec \(k\in \mathbb{R}\).
Soit \(k\) un réel et \(F\) la fonction définie pour tout réel \(x\) par \(F(x)=-\cos(x)\).
\(F\) est dérivable sur \(\mathbb{R}\) et pour tout réel \(x\), nous avons : \[ F'(x)=-\left(-\sin(x)\right)=\sin(x) \] après utilisation du Théorème 11.
Donc \(F\) est une primitive de la fonction sinus sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction sinus sont les fonctions de la forme \(x\rightarrow -\cos(x)+k\) avec \(k\in \mathbb{R}\).
Théorème 14
Soit \(u\) une fonction dérivable sur un intervalle \(I\).
Les primitives de la fonction \(x\rightarrow u'(x)\sin \left(u(x)\right)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow -\cos\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Les primitives de la fonction \(x\rightarrow u'(x)\sin \left(u(x)\right)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow -\cos\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Démonstration :
Soit \(k\) un réel et \(F=-\cos\left(u(x)\right)\).
Etant donné que \(u\) est dérivable, il en est de même pour la fonction \(F\) d'après le Théorème 12. Nous avons ainsi pour tout réel \(x\) : \[ F'(x)=-\left(-u'(x)\sin\left(u(x)\right)\right)=u'(x)\sin\left(u(x)\right) \] Donc \(F\) est une primitive de la fonction \(x\rightarrow u'(x)\sin\left(u(x)\right)\) sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction \(x\rightarrow u'(x)\sin\left(u(x)\right)\) sont les fonctions de la forme \(x\rightarrow -\cos\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Soit \(k\) un réel et \(F=-\cos\left(u(x)\right)\).
Etant donné que \(u\) est dérivable, il en est de même pour la fonction \(F\) d'après le Théorème 12. Nous avons ainsi pour tout réel \(x\) : \[ F'(x)=-\left(-u'(x)\sin\left(u(x)\right)\right)=u'(x)\sin\left(u(x)\right) \] Donc \(F\) est une primitive de la fonction \(x\rightarrow u'(x)\sin\left(u(x)\right)\) sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction \(x\rightarrow u'(x)\sin\left(u(x)\right)\) sont les fonctions de la forme \(x\rightarrow -\cos\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Théorème 15
Les primitives de la fonction \(x\rightarrow \cos(x)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow \sin(x)+k\) avec \(k\in \mathbb{R}\).
Démonstration :
Soit \(k\) un réel et \(G\) la fonction définie pour tout réel \(x\) par \(G(x)=\sin(x)\).
\(G\) est dérivable sur \(\mathbb{R}\) et pour tout réel \(x\), nous avons : \[ G'(x)=\cos(x) \] d'après le Théorème 7. Donc \(G\) est une primitive de la fonction cosinus sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction cosinus sont les fonctions de la forme \(x\rightarrow \sin(x)+k\) avec \(k\in \mathbb{R}\).
Soit \(k\) un réel et \(G\) la fonction définie pour tout réel \(x\) par \(G(x)=\sin(x)\).
\(G\) est dérivable sur \(\mathbb{R}\) et pour tout réel \(x\), nous avons : \[ G'(x)=\cos(x) \] d'après le Théorème 7. Donc \(G\) est une primitive de la fonction cosinus sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction cosinus sont les fonctions de la forme \(x\rightarrow \sin(x)+k\) avec \(k\in \mathbb{R}\).
Théorème 16
Soit \(u\) une fonction dérivable sur un intervalle \(I\).
Les primitives de la fonction \(x\rightarrow u'(x)\cos \left(u(x)\right)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow \sin\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Les primitives de la fonction \(x\rightarrow u'(x)\cos \left(u(x)\right)\) sur \(\mathbb{R}\) sont les fonctions de la forme \(x\rightarrow \sin\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Démonstration :
Soit \(k\) un réel et \(G=\sin\left(u(x)\right)\).
Etant donné que \(u\) est dérivable, il en est de même pour la fonction \(G\) d'après le Théorème 8. Nous avons ainsi pour tout réel \(x\) : \[ G'(x)=u'(x)\cos\left(u(x)\right) \] Donc \(G\) est une primitive de la fonction \(x\rightarrow u'(x)\cos\left(u(x)\right)\) sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction \(x\rightarrow u'(x)\cos\left(u(x)\right)\) sont les fonctions de la forme \(x\rightarrow \sin\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).
Soit \(k\) un réel et \(G=\sin\left(u(x)\right)\).
Etant donné que \(u\) est dérivable, il en est de même pour la fonction \(G\) d'après le Théorème 8. Nous avons ainsi pour tout réel \(x\) : \[ G'(x)=u'(x)\cos\left(u(x)\right) \] Donc \(G\) est une primitive de la fonction \(x\rightarrow u'(x)\cos\left(u(x)\right)\) sur \(\mathbb{R}\).
Ainsi toutes les primitives de la fonction \(x\rightarrow u'(x)\cos\left(u(x)\right)\) sont les fonctions de la forme \(x\rightarrow \sin\left(u(x)\right)+k\) avec \(k\in \mathbb{R}\).