FONCTIONS TRIGONOMETRIQUES
|
Exercice 1 (Nouvelle-Calédonie décembre 2019 (extrait))
Partie C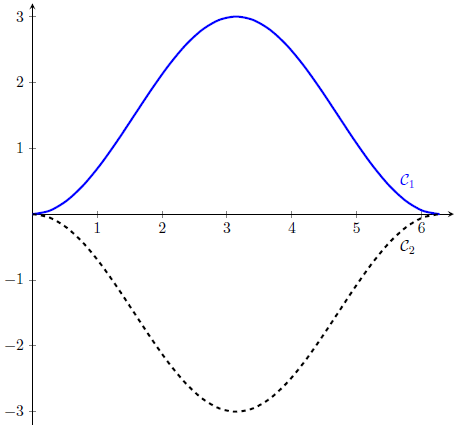
1) La fonction \(f\) est la somme de fonctions dérivables sur \(\left[0;2\pi\right]\) donc elle est dérivable sur \(\left[0;2\pi\right]\). Sa dérivée est : \[ \begin{align*} f'(x)&=-1.5\times \left(-\sin(x)\right) \\ &=1.5\sin(x). \end{align*} \] Etant donné que \(\sin(x)\) est positif lorsque \(x\in \left[0;\pi\right]\) et négatif lorsque \(x\in \left[\pi;2\pi\right]\), on en déduit que \(f'(x)\) est positif lorsque \(x\in \left[0;\pi\right]\) et négatif lorsque \(x\in \left[\pi;2\pi\right]\). Ceci implique que la fonction \(f\) est croissante sur \(\left[0;\pi\right]\) puis décroissante sur \(\left[\pi;2\pi\right]\).
On en déduit le tableau de variations de la fonction \(f\) :

Nous avons d'une part \(f(0)=-1.5\cos(0)+1.5=0\) et \(f(2\pi)=-1.5\cos(2\pi)+1.5=0\). D'après le tableau de variations, la fonction \(f\) admet deux minimums en \(0\) et \(2\pi\) qui valent 0. Donc sur l'intervalle \(\left[0;2\pi\right]\), \(f\) est positive.
2) L'aire comprise entre la courbe \(\mathcal{C}_{1}\) et l'axe des abscisses est l'intégrale de la fonction \(f\) sur l'intervalle \([0;2\pi]\).
Comme \(\mathcal{C}_{2}\) est le symétrique de \(\mathcal{C}_{1}\) par rapport à l'axe des abscisses, l'aire de la zone délimitée par les courbes \(\mathcal{C}_{1}\) et \(\mathcal{C}_{2}\) est égale à deux fois l'aire comprise entre la courbe \(\mathcal{C}_{1}\) et l'axe des abscisses.
Par conséquent : \[ \begin{align*} \mathcal{A}&=2\int_{0}^{2\pi}f(x)dx \\ &=2\int_{0}^{2\pi}-1.5\cos(x)+1.5 dx \\ &=2\left[-1.5\sin(x)+1.5x\right]_{0}^{2\pi}\\ &=2\left(-1.5\sin(2\pi)+1.5\times 2\pi-\left(-1.5\sin(0)+1.5\times 0\right)\right)\\ &=2\times 3\pi \\ &=6\pi \\ \end{align*} \] L'aire \(\mathcal{A}\) vaut \(6\pi\) unités d'aire.
Exercice 2 (Antilles Guyane juin 2018)
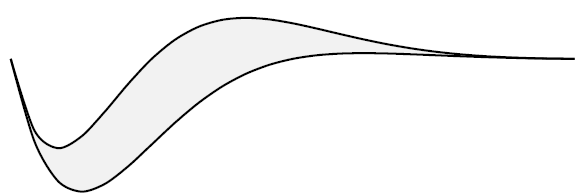
Partie A : Étude de la fonction \(f\)
1) Pour tout \(x\in \mathbb{R}\), nous avons : \[ -1\leq \cos(x) \leq 1 \] et \[ -1\leq \sin(x) \leq 1. \] Nous avons par conséquent : \[ -1\leq -\cos(x) \leq 1, \] puis : \[ -1\leq -\cos(x)+\sin(x)+1 \leq 3. \] En multipliant cette inégalité par \(e^{-x}\) qui est strictement positif pour tout \(x\) réel : \[ -e^{-x}\leq e^{-x}\left(-\cos(x)+\sin(x)+1\right) \leq 3e^{-x}, \] nous obtenons finalement l'inégalité désirée : \[ -e^{-x}\leq f(x) \leq 3e^{-x}. \]
2) Nous avons \(\lim_{x\rightarrow +\infty} e^{-x}=\lim_{X\rightarrow -\infty} e^{X}=0\).
Par conséquent, nous avons \(\lim_{x\rightarrow +\infty} 3e^{-x}=0\) et par le théorème des gendarmes, nous déduisons de l'inégalité de la question précédente que \(\lim_{x\rightarrow +\infty}f(x)=0\).
3) D'après l'énoncé, \(f\) est dérivable sur \(\mathbb{R}\) et sa dérivée est : \[ \begin{align*} f'(x)&=-e^{-x}\left(-\cos(x)+\sin(x)+1\right)+e^{-x}\left(\sin(x)+\cos(x)\right)\\ &=e^{-x}\left(\cos(x)-\sin(x)-1+\sin(x)+\cos(x)\right) \\ &=e^{-x}\left(2\cos(x)-1\right) \end{align*} \]
4)
a) Pour tout réel \(x\), nous avons \(e^{-x}>0\) donc le signe de \(f'\) est le signe de l'expression entre parenthèses.
Nous avons \(2\cos(x)-1\geq 0\) si et seulement si \(\displaystyle \cos(x)\geq \frac{1}{2}\). Avec l'aide du tableau des valeurs remarquables de la fonction cosinus, nous savons que les deux réels appartenant à l'intervalle \([−\pi;\pi]\) dont le cosinus vaut 0.5 sont \(\displaystyle -\frac{\pi}{3}\) et \(\displaystyle \frac{\pi}{3}\).
Par conséquent, \(f'(x)\geq 0\) pour tout \(\displaystyle x \in \left[-\frac{\pi}{3};\frac{\pi}{3}\right]\) et \(f'(x)\leq 0\) pour tout \(\displaystyle x\in \left[-\pi;-\frac{\pi}{3}\right]\cup \left[\frac{\pi}{3};\pi\right]\).
b) Nous avons : \[ \begin{align*} f(-\pi)&=e^{\pi}\left(-\cos(-\pi)+\sin(-\pi)+1\right)\\ &=e^{\pi}(1+0+1)\\ &=2e^{\pi} \end{align*} \] \[ \begin{align*} \displaystyle f\left(-\displaystyle \frac{\pi}{3}\right)&=e^{\left(\displaystyle \frac{\pi}{3}\right)}\left(-\cos\left(-\frac{\pi}{3}\right)+\sin\left(-\frac{\pi}{3}\right)+1\right)\\ &=\displaystyle e^{\left(\displaystyle \frac{\pi}{3}\right)}\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}+1 \right)\\ &=e^{\left(\displaystyle \frac{\pi}{3}\right)}\frac{1-\sqrt{3}}{2} \end{align*} \] \[ \begin{align*} \displaystyle f\left(\displaystyle \frac{\pi}{3}\right)&=e^{\left(\displaystyle -\frac{\pi}{3}\right)}\left(-\cos\left(\frac{\pi}{3}\right)+\sin\left(\frac{\pi}{3}\right)+1\right)\\ &=\displaystyle e^{\left(\displaystyle -\frac{\pi}{3}\right)}\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}+1 \right)\\ &=e^{\left(\displaystyle -\frac{\pi}{3}\right)}\frac{1+\sqrt{3}}{2} \end{align*} \] \[ \begin{align*} f(\pi)&=e^{-\pi}\left(-\cos(\pi)+\sin(\pi)+1\right)\\ &=e^{-\pi}(1+0+1)\\ &=2e^{-\pi} \end{align*} \] Nous pouvons à présent dresser le tableau de variations de la fonction \(f\) :

Nous avons \(2\cos(x)-1\geq 0\) si et seulement si \(\displaystyle \cos(x)\geq \frac{1}{2}\). Avec l'aide du tableau des valeurs remarquables de la fonction cosinus, nous savons que les deux réels appartenant à l'intervalle \([−\pi;\pi]\) dont le cosinus vaut 0.5 sont \(\displaystyle -\frac{\pi}{3}\) et \(\displaystyle \frac{\pi}{3}\).
Par conséquent, \(f'(x)\geq 0\) pour tout \(\displaystyle x \in \left[-\frac{\pi}{3};\frac{\pi}{3}\right]\) et \(f'(x)\leq 0\) pour tout \(\displaystyle x\in \left[-\pi;-\frac{\pi}{3}\right]\cup \left[\frac{\pi}{3};\pi\right]\).
b) Nous avons : \[ \begin{align*} f(-\pi)&=e^{\pi}\left(-\cos(-\pi)+\sin(-\pi)+1\right)\\ &=e^{\pi}(1+0+1)\\ &=2e^{\pi} \end{align*} \] \[ \begin{align*} \displaystyle f\left(-\displaystyle \frac{\pi}{3}\right)&=e^{\left(\displaystyle \frac{\pi}{3}\right)}\left(-\cos\left(-\frac{\pi}{3}\right)+\sin\left(-\frac{\pi}{3}\right)+1\right)\\ &=\displaystyle e^{\left(\displaystyle \frac{\pi}{3}\right)}\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}+1 \right)\\ &=e^{\left(\displaystyle \frac{\pi}{3}\right)}\frac{1-\sqrt{3}}{2} \end{align*} \] \[ \begin{align*} \displaystyle f\left(\displaystyle \frac{\pi}{3}\right)&=e^{\left(\displaystyle -\frac{\pi}{3}\right)}\left(-\cos\left(\frac{\pi}{3}\right)+\sin\left(\frac{\pi}{3}\right)+1\right)\\ &=\displaystyle e^{\left(\displaystyle -\frac{\pi}{3}\right)}\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}+1 \right)\\ &=e^{\left(\displaystyle -\frac{\pi}{3}\right)}\frac{1+\sqrt{3}}{2} \end{align*} \] \[ \begin{align*} f(\pi)&=e^{-\pi}\left(-\cos(\pi)+\sin(\pi)+1\right)\\ &=e^{-\pi}(1+0+1)\\ &=2e^{-\pi} \end{align*} \] Nous pouvons à présent dresser le tableau de variations de la fonction \(f\) :

Partie B : Aire du logo

1) Nous avons pour tout \(x\) réel : \[ \begin{align*} f(x)-g(x)&=e^{-x}\left(-\cos(x)+\sin(x)+1\right)-\left(-e^{-x}\cos(x)\right) \\ &=e^{-x}\left(-\cos(x)+\sin(x)+1\right)+e^{-x}\cos(x) \\ &=e^{-x}\left(-\cos(x)+\sin(x)+1+\cos(x)\right)\\ &=e^{-x}\left(\sin(x)+1\right) \end{align*} \] Etant donné que pour tout réel \(x\), nous avons \(e^{-x}>0\), le signe de \(f(x)-g(x)\) est celui de l'expression entre parenthèses.
Comme pour tout réel \(x\) nous avons \(-1\leq \sin(x) \leq 1\), nous en déduisons que \(\sin(x)+1\geq 0\) et par conséquent que \(f(x)-g(x)\geq 0\).
Ainsi, la courbe représentative de la fonction \(f\) notée \(\mathcal{C}_{f}\) est située au-dessus de celle de la fonction \(g\) notée \(\mathcal{C}_{f}\) sur \(\mathbb{R}\).
2)
a) Le domaine \(\mathcal{D}\) correspond au logo donné en début d'exercice.
b) Calcul de l'aire du domaine \(\mathcal{D}\) : \[ \begin{align*} \mathcal{D}&=\int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}}f(x)-g(x) dx \\ &=\int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-x}\left(\sin(x)+1\right)dx \\ &=\left[H(x)\right]_{-\frac{\pi}{2}}^{\frac{3\pi}{2}} \\ &=\displaystyle H\left(\frac{3\pi}{2}\right)-H\left(-\frac{\pi}{2}\right). \end{align*} \] Nous avons d'une part : \[ \begin{align*} \displaystyle H\left(\frac{3\pi}{2}\right)&=\left(-\frac{\cos \left(\frac{3\pi}{2}\right)}{2}-\frac{\sin \left(\frac{3\pi}{2}\right)}{2}-1\right)e^{-\frac{3\pi}{2}} \\ &=\left(-\frac{0}{2}-\frac{-1}{2}-1\right)e^{-\frac{3\pi}{2}} \\ &=\displaystyle -\frac{1}{2}e^{-\frac{3\pi}{2}}, \end{align*} \] et d'autre part : \[ \begin{align*} \displaystyle H\left(-\frac{\pi}{2}\right)&=\left(-\frac{\cos \left(-\frac{\pi}{2}\right)}{2}-\frac{\sin \left(-\frac{\pi}{2}\right)}{2}-1\right)e^{\frac{\pi}{2}} \\ &=\left(-\frac{0}{2}-\frac{-1}{2}-1\right)e^{\frac{\pi}{2}} \\ &=\displaystyle -\frac{1}{2}e^{\frac{\pi}{2}}. \end{align*} \] Par conséquent : \[ \begin{align*} \mathcal{D}&=\displaystyle H\left(\frac{3\pi}{2}\right)-H\left(-\frac{\pi}{2}\right)\\ &=\displaystyle -\frac{1}{2}e^{-\frac{3\pi}{2}}-\left(-\frac{1}{2}e^{\frac{\pi}{2}}\right) \\ &=\frac{e^{\frac{\pi}{2}}-e^{-\frac{3\pi}{2}}}{2}\\ &\approx 2.40\text{ unités d'aire} \end{align*} \] L'aire du logo est approximativement de 2.40 unités d'aire. Etant donné que l'unité graphique est de 2 cm, cela signifie que l'unité d'aire vaut \(2^{2}=4\) cm2.
Par conséquent, l'aire du logo est approximativement de \(2.40\times 4 \approx 9.60\) cm2.
b) Calcul de l'aire du domaine \(\mathcal{D}\) : \[ \begin{align*} \mathcal{D}&=\int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}}f(x)-g(x) dx \\ &=\int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-x}\left(\sin(x)+1\right)dx \\ &=\left[H(x)\right]_{-\frac{\pi}{2}}^{\frac{3\pi}{2}} \\ &=\displaystyle H\left(\frac{3\pi}{2}\right)-H\left(-\frac{\pi}{2}\right). \end{align*} \] Nous avons d'une part : \[ \begin{align*} \displaystyle H\left(\frac{3\pi}{2}\right)&=\left(-\frac{\cos \left(\frac{3\pi}{2}\right)}{2}-\frac{\sin \left(\frac{3\pi}{2}\right)}{2}-1\right)e^{-\frac{3\pi}{2}} \\ &=\left(-\frac{0}{2}-\frac{-1}{2}-1\right)e^{-\frac{3\pi}{2}} \\ &=\displaystyle -\frac{1}{2}e^{-\frac{3\pi}{2}}, \end{align*} \] et d'autre part : \[ \begin{align*} \displaystyle H\left(-\frac{\pi}{2}\right)&=\left(-\frac{\cos \left(-\frac{\pi}{2}\right)}{2}-\frac{\sin \left(-\frac{\pi}{2}\right)}{2}-1\right)e^{\frac{\pi}{2}} \\ &=\left(-\frac{0}{2}-\frac{-1}{2}-1\right)e^{\frac{\pi}{2}} \\ &=\displaystyle -\frac{1}{2}e^{\frac{\pi}{2}}. \end{align*} \] Par conséquent : \[ \begin{align*} \mathcal{D}&=\displaystyle H\left(\frac{3\pi}{2}\right)-H\left(-\frac{\pi}{2}\right)\\ &=\displaystyle -\frac{1}{2}e^{-\frac{3\pi}{2}}-\left(-\frac{1}{2}e^{\frac{\pi}{2}}\right) \\ &=\frac{e^{\frac{\pi}{2}}-e^{-\frac{3\pi}{2}}}{2}\\ &\approx 2.40\text{ unités d'aire} \end{align*} \] L'aire du logo est approximativement de 2.40 unités d'aire. Etant donné que l'unité graphique est de 2 cm, cela signifie que l'unité d'aire vaut \(2^{2}=4\) cm2.
Par conséquent, l'aire du logo est approximativement de \(2.40\times 4 \approx 9.60\) cm2.
Exercice 3 (Métropole - La Réunion juin 2016)
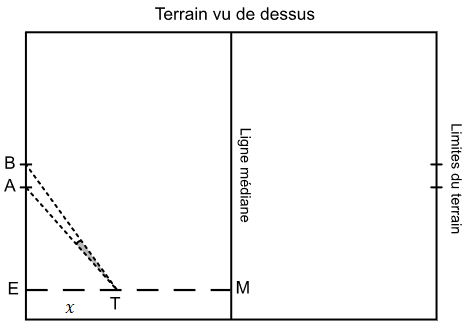
1) Le triangle \(ETA\) étant rectangle en \(E\), nous avons la relation suivante : \[ \begin{align*} \tan \alpha &= \frac{\text{côté opposé à }\widehat{ETA}}{\text{côté adjacent à }\widehat{ETA}}\\ &=\frac{AE}{ET}\\ &=\frac{25}{x}. \end{align*} \] Le triangle \(ETB\) étant rectangle en \(E\), nous avons la relation suivante : \[ \begin{align*} \tan \beta &= \frac{\text{côté opposé à }\widehat{ETB}}{\text{côté adjacent à }\widehat{ETB}}\\ &=\frac{BE}{ET}\\ &=\frac{AE+AB}{ET}\\ &=\frac{30.6}{x}. \end{align*} \]
2) La fonction \(\tan\) est le rapport de deux fonctions définies et dérivables sur \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\) et dont le dénominateur ne s'annule pas, donc la fonction \(\tan\) est dérivable sur \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\).
Nous avons : \[ \begin{align*} \left(\tan x\right)'&=\left(\frac{\sin x}{\cos x}\right)'\\ &=\frac{\cos x\times \cos x-\sin x \times (-\sin x)}{\left(\cos x\right)^{2}}\\ &=\frac{\cos^{2} x+\sin^{2} x }{\cos^{2} x}\\ &=\frac{1}{\cos^{2} x} \end{align*} \] Le dénominateur étant strictement positif (c'est un carré), on en déduit que la dérivée est strictement positive sur l’intervalle \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\) donc la fonction tangente est strictement croissante sur cet intervalle.
3) Nous avons : \[ \begin{align*} \gamma&=\widehat{ETB}-\widehat{ETA}\\ &=\beta-\alpha. \end{align*} \] Par conséquent : \[ \begin{align*} \tan \gamma &=\tan(\beta-\alpha)\\ &=\frac{\tan \beta - \tan \alpha}{1+\tan \beta \times \tan \alpha}\\ &=\frac{\displaystyle \frac{30.6}{x}-\frac{25}{x}}{1+\displaystyle \frac{30.6}{x}\times \frac{25}{x}}\\ &=\frac{\displaystyle\frac{5.6}{x}}{1+\displaystyle \frac{765}{x^{2}}}\\ &=\frac{\displaystyle\frac{5.6}{x}}{\displaystyle \frac{x^{2}+765}{x^{2}}}\\ &=\frac{5.6}{x}\times \frac{x^{2}}{x^{2}+765} \\ &=\frac{5.6x}{x^{2}+765}. \end{align*} \]
4) La fonction tangente étant strictement croissante sur \(\displaystyle \left]0 ;\frac{\pi}{2}\right[\) d'après la question 2, \(\gamma\) est maximal si et seulement si \(\tan \gamma\) est maximal.
Nous avons : \[ \begin{align*} \tan \gamma&=\frac{5.6x}{x^{2}+765} \\ &=\frac{5.6}{x+\displaystyle\frac{765}{x}}\\ &=\frac{5.6}{f(x)}, \end{align*} \] avec \(f(x)=x+\displaystyle\frac{765}{x}\).
Pour que \(\tan \gamma\) soit le plus grand possible, il faut que \(f(x)\) soit le plus petit possible. Autrement dit, il faut trouver le minimum de la fonction \(f\) sur l'intervalle \([0;50]\).
Etudions la fonction \(f\). \(f\) est dérivable et pour tout réel \(x\) nous avons : \[ \begin{align*} f'(x)&=1-\frac{765}{x^{2}}\\ &=\frac{1}{x^{2}}\left(x^{2}-765\right). \end{align*} \] Etant donné que \(\displaystyle \frac{1}{x^{2}}>0\) pour tout \(x\), le signe de \(f'\) est le signe de l'expression entre parenthèses, qui est un polynôme de degré 2.
Calcul du discriminant : \[ \Delta=0^{2}-4\times 1 \times (-765)=3060 \] Les deux racines sont : \[ \begin{align*} x_{1}=\frac{-0-\sqrt{3060}}{2\times 1}<0 \end{align*} \] et \[ \begin{align*} x_{2}&=\frac{-0+\sqrt{3060}}{2\times 1}\\ &=\frac{\sqrt{3060}}{2}\\ &=\sqrt{765}\\ &=3\sqrt{85} \end{align*} \] Nous pouvons dresser le tableau de variations de la fonction \(f\) sur l'intervalle \([0;50]\) :

Le minimum de la fonction \(f\) est atteint lorsque \(x=3\sqrt{85}\).
Par conséquent, pour maximiser \(\gamma\), il faudra choisir une valeur de \(x=3\sqrt{85}\approx 28\text{m}\).
Ceci nous donne : \[ \begin{align*} \tan \gamma &=\frac{5.6x}{x^{2}+765}\\ &\approx 0.10123 \end{align*} \] Avec la calculatrice, nous obtenons \(\gamma \approx 0.10\text{ radians}\).
Exercice 4 (Polynésie septembre 2015 (extrait))
Partie B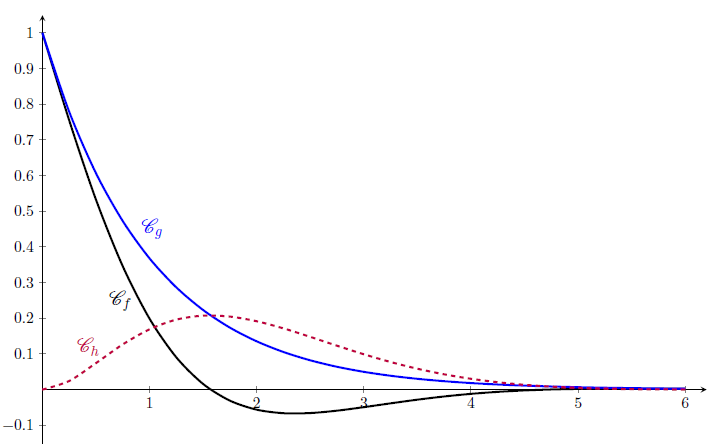
1)
a) Pour les limites des fonctions \(f\) et \(g\) en \(+\infty\), nous faisons les conjectures suivantes :
\[ \lim_{x\rightarrow +\infty} f(x)=\lim_{x\rightarrow +\infty} g(x)=0. \] b) Nous conjecturons que \(\mathscr{C}_{f}\) se situe en-dessous de \(\mathscr{C}_{g}\).
c) La valeur de l’abscisse \(x\) pour laquelle l’écart entre les deux courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\) est maximal semble être approximativement égale à 1.6.
\[ \lim_{x\rightarrow +\infty} f(x)=\lim_{x\rightarrow +\infty} g(x)=0. \] b) Nous conjecturons que \(\mathscr{C}_{f}\) se situe en-dessous de \(\mathscr{C}_{g}\).
c) La valeur de l’abscisse \(x\) pour laquelle l’écart entre les deux courbes \(\mathscr{C}_{f}\) et \(\mathscr{C}_{g}\) est maximal semble être approximativement égale à 1.6.
2) Nous allons étudier le signe de la fonction \(g-f\), c'est-à-dire la fonction \(h\), définie pour tout \(x\) réel positif par \(h(x)=e^{-x}(1-\cos x)\).
Pour tout \(x\) réel positif, nous avons \(e^{-x}>0\) et \(-1\leq \cos x \leq 1\), donc \(1-\cos x \geq 0\) ; par conséquent, la fonction \(h\) est positive pour tout \(x\) réel donc \(\mathscr{C}_{g}\) est située au-dessus de \(\mathscr{C}_{f}\) sur l’intervalle \([0 ;+\infty[\).
3) Nous avons \(\lim_{x\rightarrow +\infty}e^{-x}=\lim_{X\rightarrow -\infty}e^{X}=0\) donc \(\lim_{x\rightarrow +\infty}g(x)=0\).
Ainsi, la droite d'équation \(y=0\) est asymptote horizontale à la courbe \(\mathscr{C}_{g}\).
Nous avons : \[ -1 \leq \cos x \leq 1. \] En multipliant tous les membres de cette inéquation par \(e^{-x}\) qui est strictement positif, nous pouvons écrire : \[ -e^{-x}\leq f(x) \leq e^{-x}. \] Etant donné que \(\lim_{x\rightarrow +\infty}-e^{-x}=\lim_{x\rightarrow +\infty}e^{x}=0\), nous en déduisons par le théorème du gendarme que \(\lim_{x\rightarrow +\infty}f(x)=0\).
Ainsi, la droite d'équation \(y=0\) est aussi asymptote horizontale à la courbe \(\mathscr{C}_{f}\).
4)
a) La fonction \(h\) est définie et dérivable sur \(\mathbb{R}^{+}\) car c'est la somme de fonctions définies et dérivables sur \(\mathbb{R}^{+}\).
Nous avons : \[ \begin{align*} h'(x)&=-e^{-x}(1-\cos x)+e^{-x}\times \sin x\\ &=e^{-x}(\cos x + \sin x -1) \\ &=e^{-x}\left(\sqrt{2}\left(\frac{1}{\sqrt{2}}\cos x + \frac{1}{\sqrt{2}}\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\left(\frac{\sqrt{2}}{2}\cos x + \frac{\sqrt{2}}{2}\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\left(\cos \left(\frac{\pi}{4}\right)\cos x + \sin \left(\frac{\pi}{4}\right)\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\cos\left(\frac{\pi}{4}-x\right)-1\right)\\ &=e^{-x}\left[\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right] \end{align*} \] (Nous utilisons successivement les propriétés 11 et 5 du cours).
b) Soit \(x\in \displaystyle \left[0;\frac{\pi}{2}\right]\) : \[ 0\leq x \leq \frac{\pi}{2}. \] Alors : \[ 0-\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{\pi}{2}-\frac{\pi}{4}, \] c'est-à-dire : \[ -\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{\pi}{4}. \] Nous savons que \(\displaystyle \cos\left(-\frac{\pi}{4}\right)=\cos\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\).
En plaçant sur le cercle trigonométrique les points associés aux réels \(\displaystyle -\frac{\pi}{4}\) et \(\displaystyle \frac{\pi}{4}\) et dont l'abscisse vaut \(\displaystyle \frac{\sqrt{2}}{2}\), nous pouvons voir que pour n'importe quel angle dont la mesure est comprise entre \(\displaystyle -\frac{\pi}{4}\) et \(\displaystyle \frac{\pi}{4}\), le cosinus est supérieur à \(\displaystyle \frac{\sqrt{2}}{2}\). Autrement dit : \[ \cos \left(x-\frac{\pi}{4}\right)\geq \frac{\sqrt{2}}{2}\qquad \forall x\in \left[0;\frac{\pi}{2}\right]. \] De cette inégalité nous déduisons que sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\) : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq \sqrt{2}\frac{\sqrt{2}}{2}-1, \] et finalement : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0 \qquad\forall x\in \left[0;\frac{\pi}{2}\right]. \] A présent, prenons le cas où : \[ \frac{\pi}{2}\leq x \leq 2\pi. \] Alors : \[ \frac{\pi}{2}-\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq 2\pi-\frac{\pi}{4}, \] c'est-à-dire : \[ \frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{3\pi}{4}. \] La fonction cosinus étant décroissante sur \([0;\pi]\), nous avons : \[ \cos \left(\frac{3\pi}{4}\right)\leq \cos \left(x-\frac{\pi}{4}\right) \leq \cos \left(\frac{\pi}{4}\right), \] c'est-à-dire en particulier : \[ \cos \left(x-\frac{\pi}{4}\right) \leq \frac{\sqrt{2}}{2}. \] De cette inégalité nous déduisons que sur l’intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\) : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq \sqrt{2}\frac{\sqrt{2}}{2}-1, \] et finalement : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0 \qquad\forall x\in \left[\frac{\pi}{2};2\pi\right]. \] Nous avons bien \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0\) sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\) et \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0\) sur l'intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\).
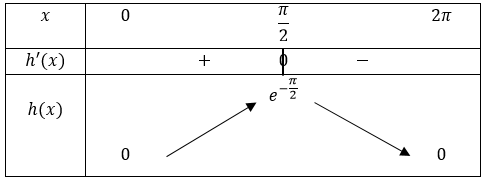
c) Quelques calculs pour le tableau de variations : \[ \begin{align*} &h(0)=e^{-0}\left(1-\cos 0\right)=0\\ &h\left(\frac{\pi}{2}\right)=e^{-\frac{\pi}{2}}\left(1-\cos \left(\frac{\pi}{2}\right)\right)=e^{-\frac{\pi}{2}}\\ &h\left(2\pi\right)=e^{-2\pi}\left(1-\cos (2\pi)\right)=0 \end{align*} \] Etant donné que \(e^{-x}>0\) pour tout réel \(x\) positif, avec les résultats de la question précédente nous avons \(\displaystyle \forall x\in \left[0;\frac{\pi}{2}\right]\): \[ e^{-x}\left(\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right)\geq 0, \] c'est-à-dire \(h'(x)\geq 0 \quad \forall x\in \displaystyle \left[0;\frac{\pi}{2}\right]\) donc la fonction \(h\) et croissante sur \(\displaystyle \left[0;\frac{\pi}{2}\right]\).
Et \(\displaystyle \forall x\in \left[\frac{\pi}{2};2\pi\right]\) nous avons : \[ e^{-x}\left(\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right)\leq 0, \] c'est-à-dire \(h'(x)\leq 0 \quad \forall x\in \displaystyle \left[\frac{\pi}{2};2\pi\right]\) donc la fonction \(h\) est décroissante sur \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\).
Nous avons à présent tous les éléments pour dresser le tableau de variations de la fonction \(h\) :
Nous avons : \[ \begin{align*} h'(x)&=-e^{-x}(1-\cos x)+e^{-x}\times \sin x\\ &=e^{-x}(\cos x + \sin x -1) \\ &=e^{-x}\left(\sqrt{2}\left(\frac{1}{\sqrt{2}}\cos x + \frac{1}{\sqrt{2}}\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\left(\frac{\sqrt{2}}{2}\cos x + \frac{\sqrt{2}}{2}\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\left(\cos \left(\frac{\pi}{4}\right)\cos x + \sin \left(\frac{\pi}{4}\right)\sin x \right) -1\right) \\ &=e^{-x}\left(\sqrt{2}\cos\left(\frac{\pi}{4}-x\right)-1\right)\\ &=e^{-x}\left[\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right] \end{align*} \] (Nous utilisons successivement les propriétés 11 et 5 du cours).
b) Soit \(x\in \displaystyle \left[0;\frac{\pi}{2}\right]\) : \[ 0\leq x \leq \frac{\pi}{2}. \] Alors : \[ 0-\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{\pi}{2}-\frac{\pi}{4}, \] c'est-à-dire : \[ -\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{\pi}{4}. \] Nous savons que \(\displaystyle \cos\left(-\frac{\pi}{4}\right)=\cos\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\).
En plaçant sur le cercle trigonométrique les points associés aux réels \(\displaystyle -\frac{\pi}{4}\) et \(\displaystyle \frac{\pi}{4}\) et dont l'abscisse vaut \(\displaystyle \frac{\sqrt{2}}{2}\), nous pouvons voir que pour n'importe quel angle dont la mesure est comprise entre \(\displaystyle -\frac{\pi}{4}\) et \(\displaystyle \frac{\pi}{4}\), le cosinus est supérieur à \(\displaystyle \frac{\sqrt{2}}{2}\). Autrement dit : \[ \cos \left(x-\frac{\pi}{4}\right)\geq \frac{\sqrt{2}}{2}\qquad \forall x\in \left[0;\frac{\pi}{2}\right]. \] De cette inégalité nous déduisons que sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\) : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq \sqrt{2}\frac{\sqrt{2}}{2}-1, \] et finalement : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0 \qquad\forall x\in \left[0;\frac{\pi}{2}\right]. \] A présent, prenons le cas où : \[ \frac{\pi}{2}\leq x \leq 2\pi. \] Alors : \[ \frac{\pi}{2}-\frac{\pi}{4}\leq x-\frac{\pi}{4} \leq 2\pi-\frac{\pi}{4}, \] c'est-à-dire : \[ \frac{\pi}{4}\leq x-\frac{\pi}{4} \leq \frac{3\pi}{4}. \] La fonction cosinus étant décroissante sur \([0;\pi]\), nous avons : \[ \cos \left(\frac{3\pi}{4}\right)\leq \cos \left(x-\frac{\pi}{4}\right) \leq \cos \left(\frac{\pi}{4}\right), \] c'est-à-dire en particulier : \[ \cos \left(x-\frac{\pi}{4}\right) \leq \frac{\sqrt{2}}{2}. \] De cette inégalité nous déduisons que sur l’intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\) : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq \sqrt{2}\frac{\sqrt{2}}{2}-1, \] et finalement : \[ \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0 \qquad\forall x\in \left[\frac{\pi}{2};2\pi\right]. \] Nous avons bien \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0\) sur l’intervalle \(\displaystyle \left[0;\frac{\pi}{2}\right]\) et \(\displaystyle \sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0\) sur l'intervalle \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\).
c) Quelques calculs pour le tableau de variations : \[ \begin{align*} &h(0)=e^{-0}\left(1-\cos 0\right)=0\\ &h\left(\frac{\pi}{2}\right)=e^{-\frac{\pi}{2}}\left(1-\cos \left(\frac{\pi}{2}\right)\right)=e^{-\frac{\pi}{2}}\\ &h\left(2\pi\right)=e^{-2\pi}\left(1-\cos (2\pi)\right)=0 \end{align*} \] Etant donné que \(e^{-x}>0\) pour tout réel \(x\) positif, avec les résultats de la question précédente nous avons \(\displaystyle \forall x\in \left[0;\frac{\pi}{2}\right]\): \[ e^{-x}\left(\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right)\geq 0, \] c'est-à-dire \(h'(x)\geq 0 \quad \forall x\in \displaystyle \left[0;\frac{\pi}{2}\right]\) donc la fonction \(h\) et croissante sur \(\displaystyle \left[0;\frac{\pi}{2}\right]\).
Et \(\displaystyle \forall x\in \left[\frac{\pi}{2};2\pi\right]\) nous avons : \[ e^{-x}\left(\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right)\leq 0, \] c'est-à-dire \(h'(x)\leq 0 \quad \forall x\in \displaystyle \left[\frac{\pi}{2};2\pi\right]\) donc la fonction \(h\) est décroissante sur \(\displaystyle \left[\frac{\pi}{2};2\pi\right]\).
Nous avons à présent tous les éléments pour dresser le tableau de variations de la fonction \(h\) :

5) Nous avons \(h(x)\geq 0\) pour tout réel positif \(x\). L’aire \(\mathscr{A}\) du domaine \(\mathscr{D}\) est ainsi égale à : \[ \begin{align*} \mathscr{A}&=\int_{0}^{2\pi}h(x)dx \\ &=\left[H(x)\right]_{0}^{2\pi} \\ &=H(2\pi)-H(0). \end{align*} \] Nous avons d'une part : \[ \begin{align*} H(2\pi)&=\frac{1}{2}e^{-2\pi}\left[-2+\cos(2\pi)-\sin(2\pi)\right] \\ &=\frac{1}{2}e^{-2\pi}\left[-2+1-0\right] \\ &=-\frac{1}{2}e^{-2\pi}, \end{align*} \] et d'autre part : \[ \begin{align*} H(0)&=\frac{1}{2}e^{-0}\left[-2+\cos(0)-\sin(0)\right] \\ &=\frac{1}{2}\left[-2+1-0\right] \\ &=-\frac{1}{2}. \end{align*} \] Finalement : \[ \begin{align*} \mathscr{A}&=H(2\pi)-H(0)\\ &=-\frac{1}{2}e^{-2\pi}-\left(-\frac{1}{2}\right) \\ &=\frac{1-e^{-2\pi}}{2} \text{ unités d'aire.} \end{align*} \]
Exercice 5 (Nouvelle-Calédonie novembre 2015 (extrait))
Partie C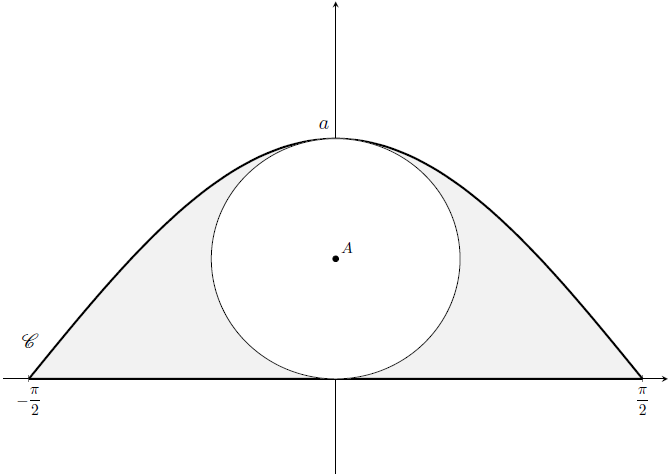
1) Soit \(\mathscr{A}\) l’aire du domaine compris entre l’axe des abscisses, les droites d’équation \(\displaystyle x=-\frac{\pi}{2}\) et \(\displaystyle x=\frac{\pi}{2}\), et la courbe \(\mathscr{C}\).
Nous avons : \[ \begin{align*} \mathscr{A}&=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}y(x) dx\\ &=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}a\cos(x) dx\\ &=a\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos(x) dx\\ &=a\left[\sin x\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\ &=a\left(\sin\left(\frac{\pi}{2}\right)-\sin\left(-\frac{\pi}{2}\right)\right) \\ &=a\left(1-(-1)\right)\\ &=2a \text{ unités d'aire} \end{align*} \]
2) L'aire du disque que l'on note \(\mathscr{D}\) est égale à : \[ \begin{align*} \mathscr{D}&=\pi R^{2}\\ &=\pi \times \left(\frac{a}{2}\right)^{2}\\ &=\pi \times \frac{a^{2}}{4}\\ &=\frac{a^{2}\pi}{4} \end{align*} \] L'aire de la surface grisée est égale à : \[ \mathscr{D}-\mathscr{A}=2a-\frac{a^{2}\pi}{4} \] On souhaite que la surface grisée soit égale à celle du disque. Ceci implique de résoudre l'équation suivante : \[ \begin{align*} &\mathscr{D}-\mathscr{A}=\mathscr{A}\\ \Leftrightarrow & 2a-\frac{a^{2}\pi}{4}=\frac{a^{2}\pi}{4}\\ \Leftrightarrow & 2a=2\frac{a^{2}\pi}{4}\\ \Leftrightarrow & a=\frac{a^{2}\pi}{4}\\ \Leftrightarrow & a=\frac{4}{\pi}*\text{ (valeur exacte)}\\ \Leftrightarrow & a\approx 1.27\text{ (valeur arrondie au centième)}\\ \end{align*} \] Il faut que \(a\) soit approximativement égal à 1.27 unités.
(*Précision : \(a=0\) n'est pas solution de l'équation car on précise dans l'énoncé que \(a\) est strictement positif.)