FONCTIONS AFFINES ET LINEAIRES
|
I) Fonction linéaire
A) Définition
Définition
On appelle fonction linéaire toute
fonction qui peut s'écrire sous la forme :
\[f:x \rightarrow ax \] Avec \(a\) un nombre connu et constant.
\[f:x \rightarrow ax \] Avec \(a\) un nombre connu et constant.
Exemple 1 :
\[ \begin{align*} f(x)&=3x\\ g(x)&=-4x\\ h(x)&=-\sqrt{2}x\\ t(x)&=\pi x \end{align*} \] Les quatre fonctions ci-dessus sont linéaires.
B) Caractérisation
1. Calcul des images et des antécédents
Une fonction linéaire se définit par son coefficient \(a\). On peut facilement déterminer
les images et les antécédents d'un nombre à partir de cette information.
Exemple 2 :
Soit \(h\) la fonction linéaire de coefficient -2. Quelle est l'image de 5 ?
On en déduit que l'expression de la fonction \(h\) est :
\[h(x)=-2x\] Et par conséquent que l'image de 5 est égale à :
\[ \begin{align*} h(5)&=-2\times 5\\ &=-10 \end{align*} \] L'image de 5 est -10.
Exemple 3 :
Soit \(t\) la fonction linéaire de coefficient 3. Quel est l'antécédent de -2 ?
On en déduit que l'expression de la fonction \(t\) est :
\[ h(x)=3x \] Et par conséquent que l'antécédent de -2 est égal à :
\[ \begin{align*} &-2=3x\\ &x=-\frac{2}{3} \end{align*} \] L'antécédent de -2 est \(\displaystyle -\frac{2}{3}\).
Exemple 2 :
Soit \(h\) la fonction linéaire de coefficient -2. Quelle est l'image de 5 ?
On en déduit que l'expression de la fonction \(h\) est :
\[h(x)=-2x\] Et par conséquent que l'image de 5 est égale à :
\[ \begin{align*} h(5)&=-2\times 5\\ &=-10 \end{align*} \] L'image de 5 est -10.
Exemple 3 :
Soit \(t\) la fonction linéaire de coefficient 3. Quel est l'antécédent de -2 ?
On en déduit que l'expression de la fonction \(t\) est :
\[ h(x)=3x \] Et par conséquent que l'antécédent de -2 est égal à :
\[ \begin{align*} &-2=3x\\ &x=-\frac{2}{3} \end{align*} \] L'antécédent de -2 est \(\displaystyle -\frac{2}{3}\).
2. Détermination de la fonction
Parfois, on sait qu'une
fonction est linéaire mais on ne connait pas son
coefficient. Nous pouvons la déterminer en connaissant un seul
couple \((x;f(x))\).
Exemple 4 :
Soit \(h\) une fonction linéaire telle que l'image de 2 soit égale à 6. Déterminer la fonction \(h\).
On sait que \(h\) est une fonction linéaire donc elle s'écrit sous la forme :
\[ h(x)=ax \] Nous savons également que :
\[ h(2)=a \times 2=6 \] Nous pouvons par conséquent en déduire \(a\) :
\[a=\frac{6}{2}=3\] La fonction \(h\) est donc une fonction linéaire de coefficient 3. On peut ainsi l'écrire de la façon suivante :
\[h(x)=3x \]
Exemple 5 :
Soit le tableau suivant :
On remarque qu'il s'agit d'un tableau de proportionnalité puisqu'on multiplie tous les membres de la première ligne par 2 pour obtenir ceux de la seconde ligne, on peut en déduire que la fonction \(f\) est égale à :
\[f(x)=2x \]
Exemple 4 :
Soit \(h\) une fonction linéaire telle que l'image de 2 soit égale à 6. Déterminer la fonction \(h\).
On sait que \(h\) est une fonction linéaire donc elle s'écrit sous la forme :
\[ h(x)=ax \] Nous savons également que :
\[ h(2)=a \times 2=6 \] Nous pouvons par conséquent en déduire \(a\) :
\[a=\frac{6}{2}=3\] La fonction \(h\) est donc une fonction linéaire de coefficient 3. On peut ainsi l'écrire de la façon suivante :
\[h(x)=3x \]
Remarque
Les fonctions linéaires représentent les
situations de proportionnalité. Le coefficient \(a\)
représente le coefficient de proportionnalité.
Exemple 5 :
Soit le tableau suivant :
| \(x\) | 2 | 3 | 5 | 6 | 8 |
| \(f(x)\) | 4 | 6 | 10 | 12 | 16 |
On remarque qu'il s'agit d'un tableau de proportionnalité puisqu'on multiplie tous les membres de la première ligne par 2 pour obtenir ceux de la seconde ligne, on peut en déduire que la fonction \(f\) est égale à :
\[f(x)=2x \]
C) Représentation graphique
Définition
La représentation graphique d'une fonction
linéaire est
une droite passant par l'origine du repère. On
appelle le paramètre \(a\) le
coefficient directeur
de la droite.
Pour déterminer graphiquement le coefficient directeur de la droite, on part d'un point donné de cette droite, on se déplace de 1 unité vers la droite et on regarde de combien on est monté ou descendu en ordonnées pour tomber sur un autre point de la droite. Cette distance correspond au coefficient directeur.
Exemple 6 :
Représenter la fonction suivante :
\[h(x)=2x \] Pour la représenter, on peut calculer quelques valeurs, renseignées dans le tableau suivant :
| \(x\) | -2 | 0 | 3 |
| \(h(x)\) | -4 | 0 | 6 |
On place ainsi les points de coordonnées (-2 ; -4) (0 ; 0) et (3 ; 6), puis on trace la droite.

Lorsqu'on prend n'importe quel point de cette droite et que l'on se déplace d'une unité vers la droite (flèche violette), on doit systématiquement monter de deux unités (flèche verte) pour tomber sur un autre point de la droite donc le coefficient directeur est bien égal à 2.
(Si on était descendu, le coefficient serait négatif).
II) Fonction affine
A) Définition
Définition
On appelle fonction affine toute
fonction qui peut s'écrire sous la forme :
\[f:x \rightarrow ax+b \] Avec \(a\) et \(b\) deux nombres connus et constants.
\[f:x \rightarrow ax+b \] Avec \(a\) et \(b\) deux nombres connus et constants.
Exemple 7 :
\[\begin{align*} f(x)&=-x+2\\ g(x)&=\frac{5}{7}x-\sqrt{3}\\ h(x)&=-\sqrt{2}x+\frac{1}{3}\\ t(x)&=\pi x-\pi \end{align*} \] Les quatre fonctions ci-dessus sont affines.
Remarque
Il existe deux cas particuliers de
fonction affine :
- lorsque \(b=0\), la fonction est linéaire. En
effet, une fonction linéaire est une fonction affine pour laquelle \(b=0\).
- lorsque \(a=0\), la fonction est constante. Tous les nombres ont la même image, égale à \(b\).
- lorsque \(a=0\), la fonction est constante. Tous les nombres ont la même image, égale à \(b\).
Exemple 8 :
La fonction \(h(x)=10\) est une fonction constante. Quel que soit \(x\) elle vaut toujours 10.
B) Caractérisation
1. Calcul des images et des antécédents
Une fonction affine se définit par son coefficient \(a\) ainsi que par le nombre \(b\). On peut facilement déterminer
les images et les antécédents d'un nombre à partir de ces informations.
Exemple 9 :
Soit \(h\) la fonction affine telle que \(a=6\) et \(b=-2\). Quelle est l'image de 2 ?
On en déduit que l'expression de la fonction \(h\) est :
\[h(x)=6x-2\] Et par conséquent que l'image de 2 est égale à :
\[ \begin{align*} h(2)&=6\times 2-2\\ &=12-2\\ &=10 \end{align*} \] L'image de 2 est 10.
Exemple 10 :
Soit \(t\) la fonction affine telle que \(a=-3\) et \(b=6\). Quelle est l'antécédent de 5 ?
On en déduit que l'expression de la fonction \(t\) est :
\[t(x)=-3x+6 \] Et par conséquent que l'antécédent de 5 est égal à :
\[ \begin{align*} &5=-3x+6\\ &-1=-3x\\ &1=3x\\ &x=\frac{1}{3} \end{align*} \] L'antécédent de 5 est \(\displaystyle \frac{1}{3}\).
Exemple 9 :
Soit \(h\) la fonction affine telle que \(a=6\) et \(b=-2\). Quelle est l'image de 2 ?
On en déduit que l'expression de la fonction \(h\) est :
\[h(x)=6x-2\] Et par conséquent que l'image de 2 est égale à :
\[ \begin{align*} h(2)&=6\times 2-2\\ &=12-2\\ &=10 \end{align*} \] L'image de 2 est 10.
Exemple 10 :
Soit \(t\) la fonction affine telle que \(a=-3\) et \(b=6\). Quelle est l'antécédent de 5 ?
On en déduit que l'expression de la fonction \(t\) est :
\[t(x)=-3x+6 \] Et par conséquent que l'antécédent de 5 est égal à :
\[ \begin{align*} &5=-3x+6\\ &-1=-3x\\ &1=3x\\ &x=\frac{1}{3} \end{align*} \] L'antécédent de 5 est \(\displaystyle \frac{1}{3}\).
2. Détermination de la fonction
Parfois, on sait qu'une
fonction est affine mais on ne connait pas son coefficient ni son
nombre.
Nous pouvons les déterminer en connaissant deux couples \((x;f(x))\) étant donné qu'il y a
deux inconnues.
Par suite, en utilisant un des couples, on détermine le paramètre \(b\).
Exemple 12 :
Soit \(h\) une fonction affine telle que l'image de 2 soit égale à 6 et l'image de 4 soit égale à 2. Déterminer la fonction \(h\).
On sait que \(h\) est une fonction affine donc elle s'écrit sous la forme :
\[h(x)=ax+b \] Nous savons également d'après l'énoncé que \(h(2)=6\) et \(h(4)=2\). Nous pouvons calculer la valeur du coefficient directeur d'après la formule précédente :
\[ \begin{align*} a&=\frac{h(4)-h(2)}{4-2}\\ &=\frac{2-6}{4-2}\\ &=\frac{-4}{2}\\ &=-2 \end{align*} \] Le coefficient directeur \(a\) de notre fonction affine est égal à -2. Nous pouvons par conséquent réécrire \(h\) de la façon suivante : \[h(x)=-2x+b\] Sachant par exemple que \(h(2)=6\) (nous pouvons aussi prendre \(h(4)=2\)), nous pouvons déterminer le coefficient \(b\) :
\[ \begin{align*} &6=-2 \times 2+b\\ &6=-4+b \\ &b=10 \end{align*} \] Le nombre \(b\) vaut 10. En conclusion :
\[h(x)=-2x+10\]
Définition
Soit \((x_{1};f(x_{1}))\)
et \((x_{2};f(x_{2}))\)
ces deux couples. Alors le coefficient directeur \(a\)
est égal à :
\[ a=\frac{f(x_{2})-f(x_{2})}{x_{2}-x_{1}} \]
\[ a=\frac{f(x_{2})-f(x_{2})}{x_{2}-x_{1}} \]
Par suite, en utilisant un des couples, on détermine le paramètre \(b\).
Exemple 12 :
Soit \(h\) une fonction affine telle que l'image de 2 soit égale à 6 et l'image de 4 soit égale à 2. Déterminer la fonction \(h\).
On sait que \(h\) est une fonction affine donc elle s'écrit sous la forme :
\[h(x)=ax+b \] Nous savons également d'après l'énoncé que \(h(2)=6\) et \(h(4)=2\). Nous pouvons calculer la valeur du coefficient directeur d'après la formule précédente :
\[ \begin{align*} a&=\frac{h(4)-h(2)}{4-2}\\ &=\frac{2-6}{4-2}\\ &=\frac{-4}{2}\\ &=-2 \end{align*} \] Le coefficient directeur \(a\) de notre fonction affine est égal à -2. Nous pouvons par conséquent réécrire \(h\) de la façon suivante : \[h(x)=-2x+b\] Sachant par exemple que \(h(2)=6\) (nous pouvons aussi prendre \(h(4)=2\)), nous pouvons déterminer le coefficient \(b\) :
\[ \begin{align*} &6=-2 \times 2+b\\ &6=-4+b \\ &b=10 \end{align*} \] Le nombre \(b\) vaut 10. En conclusion :
\[h(x)=-2x+10\]
C) Représentation graphique
Définition
La représentation graphique d'une fonction
affine est
une droite. On
appelle le paramètre \(a\) le
coefficient directeur
et le paramètre \(b\) l'ordonnée à l'origine
de la droite.
La méthode de détermination graphique du coefficient directeur est identique à celle d'une fonction linéaire. Pour l'ordonnée à l'origine (paramètre \(b\)), il suffit de lire l'ordonnée du point qui a pour abscisse 0.
Exemple 13 :
Représenter la fonction suivante :
\[h(x)=-2x+2 \] Pour la représenter, on peut calculer quelques valeurs, renseignées dans le tableau suivant :
| \(x\) | -2 | 0 | 3 |
| \(h(x)\) | 6 | 2 | -4 |
On place ainsi les points de coordonnées (-2 ; 6) (0 ; 2) et (3 ; -4), puis on trace la droite.
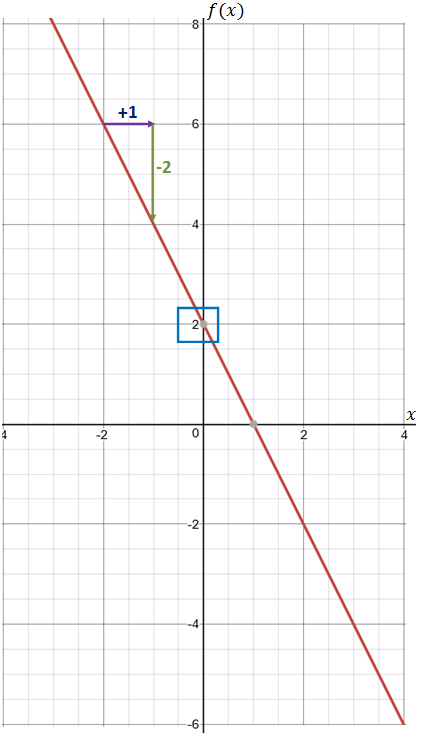
On vérifie bien qu'il s'agit d'une fonction affine : sa représentation graphique est une droite, mais elle ne passe pas par l'origine du repère.
Lorsqu'on prend n'importe quel point de cette droite et que l'on se déplace d'une unité vers la droite (flèche violette), on doit systématiquement descendre de deux unités (flèche verte) pour tomber sur un autre point de la droite donc le coefficient directeur est bien égal à -2.
Pour l'ordonnée à l'origine (paramètre \(b\)), l'ordonnée du point qui a pour abscisse 0 est 2 (cadre bleu) donc on a bien \(b=2\).