EXPONENTIELLE
|
Exercice 1 (Antilles-Guyane juin 2019)
Partie ASoit \(a\) et \(b\) des nombres réels. On considère une fonction \(f\) définie sur \([0 ;+\infty[\) par \[ f(x)=\frac{a}{1+e^{-bx}}. \] La courbe \(\mathscr{C}_{f}\) représentant la fonction \(f\) dans un repère orthogonal est donnée ci-dessous.
La courbe \(\mathscr{C}_{f}\) passe par le point \(A(0; 0,5)\). La tangente à la courbe \(\mathscr{C}_{f}\) au point \(A\) passe par le point \(B(10;1)\).

1) Justifier que \(a=1\).
On obtient alors, pour tout réel \(x\geq 0\), \[ f(x)=\frac{1}{1+e^{-bx}}. \] 2) On admet que la fonction \(f\) est dérivable sur \([0 ;+\infty[\) et on note \(f′\) sa fonction dérivée. Vérifier que, pour tout réel \(x>0\) \[ f'(x)=\frac{be^{-bx}}{\left(1+e^{-bx}\right)^{2}} \] 3) En utilisant les données de l’énoncé, détermine \(b\).
Partie B
La proportion d’individus qui possèdent un certain type d’équipement dans une population est modélisée par la fonction \(p\) définie sur \([0 ;+\infty[\) par \[ p(x)=\frac{1}{1+e^{-0.2x}}. \] Le réel \(x\) représente le temps écoulé, en année, depuis le 1er janvier 2000.
Le nombre \(p(x)\) modélise la proportion d’individus équipés après \(x\) années. Ainsi, pour ce modèle, \(p(0)\) est la proportion d’individus équipés au 1er janvier 2000 et \(p(3,5)\) est la proportion d’individus équipés au milieu de l’année 2003.
1) Quelle est, pour ce modèle, la proportion d’individus équipés au 1er janvier 2010 ? On en donnera une valeur arrondie au centième.
2)
a) Déterminer le sens de variation de la fonction \(p\) sur \([0 ;+\infty[\).
b) Calculer la limite de la fonction \(p\) en \(+\infty\).
c) Interpréter cette limite dans le contexte de l’exercice.
3) On considère que, lorsque la proportion d’individus équipés dépasse 95%, le marché est saturé.b) Calculer la limite de la fonction \(p\) en \(+\infty\).
c) Interpréter cette limite dans le contexte de l’exercice.
Déterminer, en expliquant la démarche, l’année au cours de laquelle cela se produit.
4) On définit la proportion moyenne d’individus équipés entre 2008 et 2010 par \[ m=\frac{1}{2}\int_{8}^{10}p(x)dx. \]
a) Vérifier que, pour tout réel \(x>0\),
\[
p(x)=\frac{e^{0.2x}}{1+e^{0.2x}}.
\]
b) En déduire une primitive de la fonction \(p\) sur \([0 ;+\infty[\).
c) Déterminer la valeur exacte de \(m\) et son arrondi au centième.
c) Déterminer la valeur exacte de \(m\) et son arrondi au centième.
Exercice 2 (Asie juin 2019 Partie B)
La loi de refroidissement de Newton stipule que le taux d’évolution de la température d’un corps est proportionnel à la différence entre la température de ce corps et celle du milieu environnant.Une tasse de café est servie à une température initiale de 80°C dans un milieu dont la température, exprimée en degré Celsius, supposée constante, est notée \(M\).
Le but de cet exercice est d’étudier le refroidissement du café en appliquant la loi de Newton.
Pour tout réel \(t\) positif ou nul, on note \(\theta(t)\) la température du café à l’instant \(t\), avec \(\theta(t)\) exprimé en degré Celsius et \(t\) en minute. On a ainsi \(\theta(0)=80\).
Dans ce modèle, on suppose que \(\theta\) est une fonction dérivable sur l’intervalle \([0 ;+\infty[\) et que, pour tout réel \(t\) de cet intervalle, la loi de Newton se modélise par l’égalité : \[ \theta'(t)=-0.2\left(\theta(t)-M\right). \] 1) Dans cette question, on choisit \(M=0\). On cherche alors une fonction \(\theta\) dérivable sur l’intervalle \([0 ;+\infty[\) vérifiant \(\theta(0)=80\) et, pour tout réel \(t\) de cet intervalle : \(\theta′(t)=−0,2\theta(t)\).
a) Si \(\theta\) est une telle fonction, on pose pour tout \(t\) de l’intervalle \([0 ;+\infty[\),
\[
f(t)=\frac{\theta(t)}{e^{-0.2t}}.
\]
Montrer que la fonction \(f\) est dérivable sur \([0 ;+\infty[\) et que, pour tout réel \(t\) de cet intervalle, \(f′(t)=0\).
b) En conservant l’hypothèse du a), calculer \(f(0)\). En déduire, pour tout \(t\) de l’intervalle \([0 ;+\infty[\) , une expression de \(f(t)\), puis de \(\theta(t)\).
c) Vérifier que la fonction \(\theta\) trouvée en b) est solution du problème.
2) Dans cette question, on choisit \(M=10\). On admet qu’il existe une unique fonction \(g\) dérivable sur \([0 ;+\infty[\), modélisant la température du café à tout instant positif \(t\), et que, pour tout \(t\) de l’intervalle \([0 ;+\infty[\) :
\[
g(t)=10+70e^{-0.2t},
\]
où \(t\) est exprimé en minute et \(g(t)\) en degré Celsius. b) En conservant l’hypothèse du a), calculer \(f(0)\). En déduire, pour tout \(t\) de l’intervalle \([0 ;+\infty[\) , une expression de \(f(t)\), puis de \(\theta(t)\).
c) Vérifier que la fonction \(\theta\) trouvée en b) est solution du problème.
Une personne aime boire son café à 40 °C.
Montrer qu’il existe un unique réel \(t_{0}\) dans \([0 ;+\infty[\) tel que \(g(t_{0})=40\).
Donner la valeur de \(t_{0}\) arrondie à la seconde.
Exercice 3 (Métropole-La Réunion juin 2019)
Partie AOn considère la fonction \(f\) définie sur l’ensemble \(\mathbb{R}\) des nombres réels par : \[ f(x)=\frac{7}{2}-\frac{1}{2}\left(e^{x}+e^{-x}\right). \] 1)
a) Déterminer la limite de la fonction \(f\) en \(+\infty\).
b) Montrer que la fonction \(f\) est strictement décroissante sur l’intervalle \([0 ;+\infty[\).
c) Montrer que l’équation \(f(x)=0\) admet, sur l’intervalle \([0 ;+\infty[\), une unique solution, que l’on note \(\alpha\).
2) En remarquant que, pour tout réel \(x\), \(f(−x)=f(x)\), justifier que l’équation \(f(x)=0\) admet exactement deux solutions dans \(\mathbb{R}\) et qu’elles sont opposées. b) Montrer que la fonction \(f\) est strictement décroissante sur l’intervalle \([0 ;+\infty[\).
c) Montrer que l’équation \(f(x)=0\) admet, sur l’intervalle \([0 ;+\infty[\), une unique solution, que l’on note \(\alpha\).
Partie B
Les serres en forme de tunnel sont fréquemment utilisées pour la culture des plantes fragiles ; elles limitent les effets des intempéries ou des variations de température.
Elles sont construites à partir de plusieurs arceaux métalliques identiques qui sont ancrés au sol et supportent une bâche en plastique.
Le plan est rapporté à un repère orthonormé d’unité 1 mètre. La fonction \(f\) et le réel \(\alpha\) sont définis dans la partie A. Dans la suite de l’exercice, on modélise un arceau de serre par la courbe \(\mathscr{C}\) de la fonction \(f\) sur l’intervalle \([−\alpha;+\alpha]\).
On a représenté ci-dessous la courbe \(\mathscr{C}\) sur l’intervalle \([−\alpha;+\alpha]\).

On admettra que la courbe \(\mathscr{C}\) admet l’axe des ordonnées pour axe de symétrie.
1) Calculer la hauteur d’un arceau.
2)
a) Dans cette question, on se propose de calculer la valeur exacte de la longueur de la courbe \(\mathscr{C}\) sur l’intervalle \([0 ;\alpha]\). On admet que cette longueur est donnée, en mètre, par l’intégrale :
\[
I=\int_{0}^{\alpha}\sqrt{1+\left(f'(x)\right)^{2}}dx
\]
Montrer que, pour tout réel \(x\), on a :
\[
1+\left(f'(x)\right)^{2}=\frac{1}{4}\left(e^{x}+e^{-x}\right)^{2}
\]
b) En déduire la valeur de l’intégrale \(I\) en fonction de \(\alpha\).
Justifier que la longueur d’un arceau, en mètre, est égale à : \(e^{\alpha}-e^{-\alpha}\).
Justifier que la longueur d’un arceau, en mètre, est égale à : \(e^{\alpha}-e^{-\alpha}\).
Partie C
On souhaite construire une serre de jardin en forme de tunnel.
On fixe au sol quatre arceaux métalliques, dont la forme est celle décrite dans la partie précédente, espacés de 1,5 mètre, comme indiqué sur le schéma ci-dessous.
Sur la façade sud, on prévoit une ouverture modélisée sur le schéma par le rectangle ABCD de largeur 1 mètre et de longueur 2 mètres.
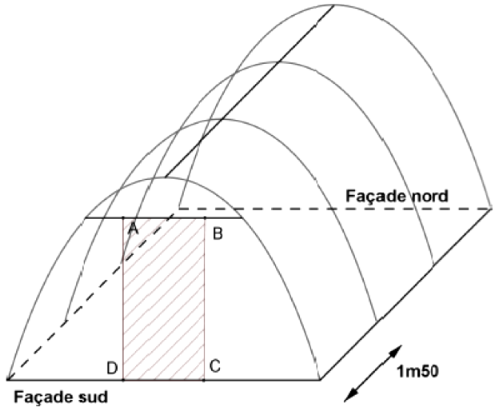
On souhaite connaître la quantité, exprimée en m2, de bâche plastique nécessaire pour réaliser cette serre.
Cette bâche est constituée de trois parties, l’une recouvrant la façade nord, l’autre la façade sud (sauf l’ouverture), la troisième partie de forme rectangulaire recouvrant le toit de la serre.
1) Montrer que la quantité de bâche nécéssaire pour recouvrir les façades sud et nord est donnée, en m2, par : \[ \mathscr{A}=4\int_{0}^{\alpha}f(x)dx-2 \] 2) On prend 1,92 pour valeur approchée de \(\alpha\). Déterminer, au m2 près, l’aire totale de la bâche plastique nécessaire pour réaliser cette serre.
Exercice 4 (Amérique du Sud Novembre 2019)
La vasopressine est une hormone favorisant la réabsorption de l’eau par l’organisme.Le taux de vasopressine dans le sang est considéré normal s’il est inférieur à 2,5μg/mL.
Cette hormone est sécrétée dès que le volume sanguin diminue. En particulier, il y a production de vasopressine suite à une hémorragie.
On utilisera dans la suite la modélisation suivante : \[ f(t)=3te^{-\frac{1}{4}t}+2\text{ avec } t\geq 0, \] où \(f(t)\) représente le taux de vasopressine (en μg/mL) dans le sang en fonction du temps \(t\) (en minute) écoulé après le début d’une hémorragie.
1)
a) Quel est le taux de vasopressine dans le sang à l’instant \(t=0\) ?
b) Justifier que douze secondes après une hémorragie, le taux de vasopressine dans le sang n’est pas normal.
c) Déterminer la limite de la fonction \(f\) en \(+\infty\). Interpréter ce résultat.
2) On admet que la fonction \(f\) est dérivable sur \([0 ;+\infty[\). b) Justifier que douze secondes après une hémorragie, le taux de vasopressine dans le sang n’est pas normal.
c) Déterminer la limite de la fonction \(f\) en \(+\infty\). Interpréter ce résultat.
Vérifier que pour tout nombre réel \(t\) positif, \[ f'(t)=\frac{3}{4}(4-t)e^{-\frac{1}{4}t}. \] 3)
a) Étudier le sens de variation de \(f\) sur l’intervalle \([0 ;+\infty[\) et dresser le tableau de variations de la fonction \(f\) (en incluant la limite en \(+\infty\)).
b) À quel instant le taux de vasopressine est-il maximal ?
Quel est alors ce taux ? On en donnera une valeur approchée à 10−2 près.
4)
b) À quel instant le taux de vasopressine est-il maximal ?
Quel est alors ce taux ? On en donnera une valeur approchée à 10−2 près.
a) Démontrer qu’il existe une unique valeur \(t_{0}\) appartenant à \([0 ; 4]\) telle que \(f(t_{0})=2.5\).
En donner une valeur approchée à 10−3 près.
En donner une valeur approchée à 10−3 près.
On admet qu’il existe une unique valeur \(t_{1}\) appartenant à \([4 ;+\infty[\) vérifiant \(f(t_{1})=2.5\).
On donne une valeur approchée de \(t_{1}\) à 10−3 près : \(t_{1}≈18,930\).
b) Déterminer pendant combien de temps, chez une personne victime d’une hémorragie, le taux de vasopressine reste supérieur à 2,5μg/mL dans le sang.
5) Soit \(F\) la fonction définie sur \([0 ;+\infty[\) par \[ F(t)=-12(t+4)e^{-\frac{1}{4}t}+2t. \]
a) Démontrer que la fonction \(F\) est une primitive de la fonction \(f\) et en déduire une valeur approchée de \(\displaystyle \int_{t_{0}}^{t_{1}}f(t)dt\) à l'unité près.
b) En déduire une valeur approchée à 0.1 près du taux moyen de vasopressine, lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL.
b) En déduire une valeur approchée à 0.1 près du taux moyen de vasopressine, lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL.
Exercice 5 (Nouvelle Calédonie février 2020)
Partie AOn considère la fonction \(f\) définie sur l’intervalle \([0 ;+\infty[\) par \[ f(x)=(ax+b)e^{-\frac{1}{2}x}, \] où \(a\) et \(b\) désignent deux nombres réels. On admet que cette fonction est dérivable sur l’intervalle \([0 ;+\infty[\) et on note \(f′\) sa fonction dérivée. Sa courbe représentative \(\mathscr{C}_{f}\) est tracée ci-dessous.

Elle coupe l’axe des ordonnées au point d’ordonnée 1 et admet une tangente horizontale au point d’abscisse 1.
1) Donner les valeurs de \(f(0)\) et \(f′(1)\).
2) Démontrer que, pour tout réel positif \(x\), \[ f'(x)=\left(-\frac{1}{2}ax-\frac{1}{2}b+a\right)e^{-\frac{1}{2}x}. \] 3) Déterminer les valeurs de \(a\) et \(b\).
Partie B
Pour la suite de l’exercice, on admet que la fonction \(f\) est définie sur \([0 ;+\infty[\) par : \[ f(x)=(x+1)e^{-\frac{1}{2}x}. \] 1)
a) Justifier que, pour tout réel \(x\) positif,
\[
f(x)=2\left(\frac{\frac{1}{2}x}{e^{\frac{1}{2}x}}\right)+e^{-\frac{1}{2}x}.
\]
b) Calculer la limite de la fonction \(f\) en \(+\infty\).
2) Étudier les variations de la fonction \(f\) sur \([0 ;+\infty[\) et construire son tableau de variations. 3) Démontrer que l’équation \(f(x)=0,07\) admet une unique solution \(\alpha\) sur l’intervalle \([0 ;+\infty[\).
4) Donner l'arrondi de \(\alpha\) à l'unité.
Partie C - Modélisation d'un tas de sable
Dans cette partie, on considère que la courbe de la fonction \(f\) modélise le profil d’un tas de sable.
La longueur \(x\) et la hauteur \(f(x)\) sont exprimées en mètres.
Ainsi, le fait que \(f(0)=1\) signifie qu’à son extrémité gauche, la hauteur du tas de sable est de 1 mètre.
On souhaite que le tas de sable soit limité par deux murs comme indiqué sur le schéma ci-dessous.
Le mur de gauche coïncide avec l’axe des ordonnées et le mur de droite est placé de telle sorte que la hauteur de sable à cet endroit est de 7 cm.

1) Pourquoi le mur de droite doit-il être placé à environ 10 mètres du mur de gauche ?
2) Vérifier que la fonction \(G\) définie sur \([0; 10]\) par \(G(x)=(-2x-4)e^{-\frac{1}{2}x}\) est une primitive de la fonction \(g\) définie sur \([0; 10]\) par \(g(x)=xe^{−\frac{1}{2}x}\).
3) En déduire une primitive de la fonction \(f\) sur l’intervalle \([0; 10]\).
4) Pour pouvoir créer un terrain de sport sur sable, on décide de niveler le tas de sable, c’est-à-dire de l’étaler à une même hauteur entre les deux murs.
Quelle sera la hauteur du tas de sable une fois le nivellement réalisé ? Expliquer le raisonnement et arrondir le résultat au centimètre.