EXPONENTIELLE
|
I) Définition
Définition 1
Il existe une unique fonction définie et dérivable sur \(\mathbb{R}\), égale à sa dérivée et prenant la valeur 1 en 0.
Cette fonction est appelée exponentielle et se note \(\exp\).
Par définition, pour tout réel \(x\), nous avons : \[ \begin{align*} &\exp'(x)=\exp(x) \text{ et } \exp(0)=1 \end{align*} \]
Cette fonction est appelée exponentielle et se note \(\exp\).
Par définition, pour tout réel \(x\), nous avons : \[ \begin{align*} &\exp'(x)=\exp(x) \text{ et } \exp(0)=1 \end{align*} \]
Démonstration
En terminale, nous n'avons pas encore les connaissances pour démontrer l'existence d'une telle fonction. Nous nous contenterons ici de démontrer l'unicité de cette fonction.
Partie 1
Nous allons devoir démontrer tout d'abord que pour tout \(x\) réel : \[ \exp(x)\times \exp(-x)=1, \] et par conséquent \(\exp(x)\neq 0\) \(\forall x\in \mathbb{R}\).
Pour démontrer ceci, nous considérons la fonction \(g\) définie sur \(\mathbb{R}\) par \[ g(x)=\exp(x)\times \exp(-x), \qquad \forall x\in \mathbb{R}. \] \(g\) est dérivable sur \(\mathbb{R}\) car c'est le produit de deux fonctions dérivables sur \(\mathbb{R}\). Nous avons \(\forall x\in \mathbb{R}\) : \[ \begin{align*} g'(x)&=\left(\exp(x)\right)' \times \exp(-x)+\exp(x)\times \left(\exp(-x)\right)' \\ &=\exp(x)\times \exp(-x)+\exp(x)\times \exp(-x)\times (-1) \end{align*} \] (on utilise la propriété sur la dérivée de fonctions composées : \(\left(f\left(u(x)\right)\right)'=f'\left(u(x)\right)u'(x)\), avec \(u(x)=-x\) et \(f(x)=\exp(x)\). )
Reprenons notre calcul : \[ \begin{align*} g'(x)&=\exp(x)\times \exp(-x)+\exp(x)\times \exp(-x)\times (-1) \\ &=\exp(x)\times \exp(-x)-\exp(x)\times \exp(-x)\\ &=0 \end{align*} \] Puisque la dérivée de la fonction \(g\) est nulle pour tout \(x\) réel, cela signifie que \(g\) est une fonction constante sur \(\mathbb{R}\).
En particulier : \[ \begin{align*} g(x)&=g(0) \quad \forall x \in \mathbb{R}\\ &=\exp(0)\times \exp(-0)\\ &=\exp(0)\times \exp(0)\\ &=1\times 1\\ &=1. \end{align*} \] Par conséquent, pour tout réel \(x\), nous avons \[ \exp(x)\times \exp(-x)=1, \] et \(\exp(x)\neq 0, \forall x\in \mathbb{R}\).
Partie 2
Nous allons à présent démontrer l'unicité.
Soit \(f\) une fonction définie et dérivable sur \(\mathbb{R}\) vérifiant \(f'=f\) et \(f(0)=1\).
Considérons la fonction \(h\) définie sur \(\mathbb{R}\) par : \[ h(x)=\frac{f(x)}{\exp(x)} \] (Nous avons vu dans la première partie que \(\exp(x)\neq 0 \forall x \in \mathbb{R}\), donc le dénominateur de \(h\) ne s'annule pas.)
Nous avons pour tout réel \(x\) : \[ \begin{align*} h'(x)&=\frac{f'(x)\times \exp(x)-f(x)\times \left(\exp(x)\right)'}{\left(\exp(x)\right)^{2}}\\ &=\frac{f'(x)\times \exp(x)-f(x)\times \exp(x)}{\left(\exp(x)\right)^{2}}\text{ car }\left(\exp(x)\right)'=\exp(x)\\ &=\frac{f(x)\times \exp(x)-f(x)\times \exp(x)}{\left(\exp(x)\right)^{2}}\text{ car } f'=f\\ &=0 \end{align*} \] La dérivée de la fonction \(h\) est nulle pour tout réel \(x\), donc \(h\) est constante sur \(\mathbb{R}\).
En particulier, \[ \begin{align*} h(x)&=h(0) \quad \forall x \in \mathbb{R} \\ &=\frac{f(0)}{\exp(0)}\\ &=\frac{1}{1}\\ &=1 \end{align*} \] Puisque \(h(x)=1\) pour tout réel \(x\), cela signifie que \(f(x)=\exp(x)\).
Nous avons bien démontré l'unicité.
En terminale, nous n'avons pas encore les connaissances pour démontrer l'existence d'une telle fonction. Nous nous contenterons ici de démontrer l'unicité de cette fonction.
Partie 1
Nous allons devoir démontrer tout d'abord que pour tout \(x\) réel : \[ \exp(x)\times \exp(-x)=1, \] et par conséquent \(\exp(x)\neq 0\) \(\forall x\in \mathbb{R}\).
Pour démontrer ceci, nous considérons la fonction \(g\) définie sur \(\mathbb{R}\) par \[ g(x)=\exp(x)\times \exp(-x), \qquad \forall x\in \mathbb{R}. \] \(g\) est dérivable sur \(\mathbb{R}\) car c'est le produit de deux fonctions dérivables sur \(\mathbb{R}\). Nous avons \(\forall x\in \mathbb{R}\) : \[ \begin{align*} g'(x)&=\left(\exp(x)\right)' \times \exp(-x)+\exp(x)\times \left(\exp(-x)\right)' \\ &=\exp(x)\times \exp(-x)+\exp(x)\times \exp(-x)\times (-1) \end{align*} \] (on utilise la propriété sur la dérivée de fonctions composées : \(\left(f\left(u(x)\right)\right)'=f'\left(u(x)\right)u'(x)\), avec \(u(x)=-x\) et \(f(x)=\exp(x)\). )
Reprenons notre calcul : \[ \begin{align*} g'(x)&=\exp(x)\times \exp(-x)+\exp(x)\times \exp(-x)\times (-1) \\ &=\exp(x)\times \exp(-x)-\exp(x)\times \exp(-x)\\ &=0 \end{align*} \] Puisque la dérivée de la fonction \(g\) est nulle pour tout \(x\) réel, cela signifie que \(g\) est une fonction constante sur \(\mathbb{R}\).
En particulier : \[ \begin{align*} g(x)&=g(0) \quad \forall x \in \mathbb{R}\\ &=\exp(0)\times \exp(-0)\\ &=\exp(0)\times \exp(0)\\ &=1\times 1\\ &=1. \end{align*} \] Par conséquent, pour tout réel \(x\), nous avons \[ \exp(x)\times \exp(-x)=1, \] et \(\exp(x)\neq 0, \forall x\in \mathbb{R}\).
Partie 2
Nous allons à présent démontrer l'unicité.
Soit \(f\) une fonction définie et dérivable sur \(\mathbb{R}\) vérifiant \(f'=f\) et \(f(0)=1\).
Considérons la fonction \(h\) définie sur \(\mathbb{R}\) par : \[ h(x)=\frac{f(x)}{\exp(x)} \] (Nous avons vu dans la première partie que \(\exp(x)\neq 0 \forall x \in \mathbb{R}\), donc le dénominateur de \(h\) ne s'annule pas.)
Nous avons pour tout réel \(x\) : \[ \begin{align*} h'(x)&=\frac{f'(x)\times \exp(x)-f(x)\times \left(\exp(x)\right)'}{\left(\exp(x)\right)^{2}}\\ &=\frac{f'(x)\times \exp(x)-f(x)\times \exp(x)}{\left(\exp(x)\right)^{2}}\text{ car }\left(\exp(x)\right)'=\exp(x)\\ &=\frac{f(x)\times \exp(x)-f(x)\times \exp(x)}{\left(\exp(x)\right)^{2}}\text{ car } f'=f\\ &=0 \end{align*} \] La dérivée de la fonction \(h\) est nulle pour tout réel \(x\), donc \(h\) est constante sur \(\mathbb{R}\).
En particulier, \[ \begin{align*} h(x)&=h(0) \quad \forall x \in \mathbb{R} \\ &=\frac{f(0)}{\exp(0)}\\ &=\frac{1}{1}\\ &=1 \end{align*} \] Puisque \(h(x)=1\) pour tout réel \(x\), cela signifie que \(f(x)=\exp(x)\).
Nous avons bien démontré l'unicité.
Notation
Pour tout réel \(x\), l'exponentielle de \(x\) peut se noter indifféremment \(\exp(x)\) ou \(e^{x}\).
En particulier, nous avons \(e^{1}=e\approx 2.718\).
II) Propriétés algébriques
Propriété 1
Pour tout \(a\in \mathbb{R}\) et \(b\in \mathbb{R}\) :
\[
\exp(a+b)=\exp(a)\times \exp(b).
\]
Démonstration
Soit \(b\) un réel fixé. D'après la démonstration Partie 1 de la définition 1, nous savons que \(\exp(b)\neq 0\).
Soit \(g\) la fonction définie pour tout réel \(a\) par : \[ g(a)=\frac{\exp(a+b)}{\exp(b)} \] Notons que le dénominateur est une constante (il ne dépend pas de \(a\)), et il est strictement différent de 0.
Nous avons d'une part : \[ \begin{align*} g'(a)&=\frac{\left(\exp(a+b)\right)'}{\exp(b)}\\ &=\frac{\exp(a+b)}{\exp(b)}\\ &=g(a), \end{align*} \] et d'autre part : \[ \begin{align*} g(0)&=\frac{\exp(0+b)}{\exp(b)}\\ &=\frac{\exp(b)}{\exp(b)}\\ &=1. \end{align*} \] \(g\) est une fonction définie et dérivable sur \(\mathbb{R}\) telle que \(g'=g\) et \(g(0)=1\), donc \(g\) est la fonction exponentielle d'après la définition 1.
On en déduit que pour tout réel \(a\) : \[ g(a)=\exp(a) \] c'est-à-dire \[ \frac{\exp(a+b)}{\exp(b)}=\exp(a), \] et finalement la Propriété 1 : \[ \exp(a+b)=\exp(a)\times \exp(b) \]
Soit \(b\) un réel fixé. D'après la démonstration Partie 1 de la définition 1, nous savons que \(\exp(b)\neq 0\).
Soit \(g\) la fonction définie pour tout réel \(a\) par : \[ g(a)=\frac{\exp(a+b)}{\exp(b)} \] Notons que le dénominateur est une constante (il ne dépend pas de \(a\)), et il est strictement différent de 0.
Nous avons d'une part : \[ \begin{align*} g'(a)&=\frac{\left(\exp(a+b)\right)'}{\exp(b)}\\ &=\frac{\exp(a+b)}{\exp(b)}\\ &=g(a), \end{align*} \] et d'autre part : \[ \begin{align*} g(0)&=\frac{\exp(0+b)}{\exp(b)}\\ &=\frac{\exp(b)}{\exp(b)}\\ &=1. \end{align*} \] \(g\) est une fonction définie et dérivable sur \(\mathbb{R}\) telle que \(g'=g\) et \(g(0)=1\), donc \(g\) est la fonction exponentielle d'après la définition 1.
On en déduit que pour tout réel \(a\) : \[ g(a)=\exp(a) \] c'est-à-dire \[ \frac{\exp(a+b)}{\exp(b)}=\exp(a), \] et finalement la Propriété 1 : \[ \exp(a+b)=\exp(a)\times \exp(b) \]
Propriété 2
Pour tout \(a\in \mathbb{R}\) :
\[
\exp(-a)=\frac{1}{\exp(a)}.
\]
Démonstration :
Cela provient directement de la démonstration de la Définition 1, partie 1. En effet, nous avions démontré que pour tout réel \(a\) : \[ \exp(a)\times \exp(-a)=1, \] d'où nous obtenons : \[ \exp(-a)=\frac{1}{\exp(a)}. \]
Cela provient directement de la démonstration de la Définition 1, partie 1. En effet, nous avions démontré que pour tout réel \(a\) : \[ \exp(a)\times \exp(-a)=1, \] d'où nous obtenons : \[ \exp(-a)=\frac{1}{\exp(a)}. \]
Propriété 3
Pour tout \(a\in \mathbb{R}\) et tout \(b\in \mathbb{R}\) :
\[
\exp(a-b)=\frac{\exp(a)}{\exp(b)}
\]
Démonstration :
Nous pouvons démontrer cette propriété en utilisant les propriétés 1 et 2. En effet, pour tout \(a\in \mathbb{R}\) et tout \(b\in \mathbb{R}\) nous avons \[ \begin{align*} \exp(a-b)&=\exp\left(a+(-b)\right)\\ &=\exp(a)\times \exp(-b) \text{ (d'après la Propriété 1)}\\ &=\exp(a)\times \frac{1}{\exp(b)} \text{ (d'après la Propriété 2)} \\ &=\frac{\exp(a)}{\exp(b)}. \end{align*} \] Nous avons bien \(\displaystyle \exp(a-b)=\frac{\exp(a)}{\exp(b)}\), soit la propriété 3.
Nous pouvons démontrer cette propriété en utilisant les propriétés 1 et 2. En effet, pour tout \(a\in \mathbb{R}\) et tout \(b\in \mathbb{R}\) nous avons \[ \begin{align*} \exp(a-b)&=\exp\left(a+(-b)\right)\\ &=\exp(a)\times \exp(-b) \text{ (d'après la Propriété 1)}\\ &=\exp(a)\times \frac{1}{\exp(b)} \text{ (d'après la Propriété 2)} \\ &=\frac{\exp(a)}{\exp(b)}. \end{align*} \] Nous avons bien \(\displaystyle \exp(a-b)=\frac{\exp(a)}{\exp(b)}\), soit la propriété 3.
Propriété 4
Pour tout \(a\in \mathbb{R}\) et tout \(n\in \mathbb{Z}\) :
\[
\left(\exp(a)\right)^{n}=\exp(an)
\]
Démonstration :
Nous allons démontrer cette propriété par récurrence et à l'aide de la Propriété 1. Nous considérons d'abord le cas \(n\in \mathbb{N}\).
Initialisation : \(n=0\)
Pour tout \(a\in \mathbb{R}\), \[ \left(\exp(a)\right)^{0}=1=\exp(0)=\exp(a\times 0) \] donc la propriété est vraie au rang 0.
Hérédité : Supposons la propriété vraie au rang \(n\). Alors pour tout \(a\in \mathbb{R}\) : \[ \begin{align*} \left(\exp(a)\right)^{n+1}&=\left(\exp(a)\right)^{n}\times \exp(a) \\ &=\exp(an)\times\exp(a) \text{ (par hypothèse de récurrence)}\\ &=\exp (an\times a) \text{ (d'après la Propriété 1)}\\ &=\exp \left(a(n+1)\right) \end{align*} \] donc la propriété est vraie au rang \(n+1\).
Conclusion : \(\forall a\in \mathbb{R}\), \(\forall n\in \mathbb{N}\), nous avons \(\left(\exp (a)\right)^{n}=\exp(an)\).
Dans le cas où \(n\) est un entier relatif négatif, nous allons utiliser la Propriété 2 pour démontrer le résultat voulu. En effet, pour tout \(a\in \mathbb{R}\) : \[ \begin{align*} \exp(a^{n})&=\frac{1}{\exp \left(a^{-n}\right)} \text{ (d'après la Propriété 2)} \\ &=\frac{1}{\exp(-an)} \\ &=\exp(an) \text{ (d'après la Propriété 2)} \end{align*} \] car \(-n\) est positif et d'après la récurrence précédente. La propriété est également vraie pour les entiers relatifs négatifs.
Nous avons bien \(\forall a\in \mathbb{R}\), \(\forall n\in \mathbb{Z}\), \(\exp (a^{n})=\exp(an)\), soit la Propriété 4.
Nous allons démontrer cette propriété par récurrence et à l'aide de la Propriété 1. Nous considérons d'abord le cas \(n\in \mathbb{N}\).
Initialisation : \(n=0\)
Pour tout \(a\in \mathbb{R}\), \[ \left(\exp(a)\right)^{0}=1=\exp(0)=\exp(a\times 0) \] donc la propriété est vraie au rang 0.
Hérédité : Supposons la propriété vraie au rang \(n\). Alors pour tout \(a\in \mathbb{R}\) : \[ \begin{align*} \left(\exp(a)\right)^{n+1}&=\left(\exp(a)\right)^{n}\times \exp(a) \\ &=\exp(an)\times\exp(a) \text{ (par hypothèse de récurrence)}\\ &=\exp (an\times a) \text{ (d'après la Propriété 1)}\\ &=\exp \left(a(n+1)\right) \end{align*} \] donc la propriété est vraie au rang \(n+1\).
Conclusion : \(\forall a\in \mathbb{R}\), \(\forall n\in \mathbb{N}\), nous avons \(\left(\exp (a)\right)^{n}=\exp(an)\).
Dans le cas où \(n\) est un entier relatif négatif, nous allons utiliser la Propriété 2 pour démontrer le résultat voulu. En effet, pour tout \(a\in \mathbb{R}\) : \[ \begin{align*} \exp(a^{n})&=\frac{1}{\exp \left(a^{-n}\right)} \text{ (d'après la Propriété 2)} \\ &=\frac{1}{\exp(-an)} \\ &=\exp(an) \text{ (d'après la Propriété 2)} \end{align*} \] car \(-n\) est positif et d'après la récurrence précédente. La propriété est également vraie pour les entiers relatifs négatifs.
Nous avons bien \(\forall a\in \mathbb{R}\), \(\forall n\in \mathbb{Z}\), \(\exp (a^{n})=\exp(an)\), soit la Propriété 4.
III) Propriétés analytiques
Théorème 1
La fonction exponentielle est stritement positive sur \(\mathbb{R}\)
\[
\exp(x) >0 \quad \forall x\in \mathbb{R}.
\]
Démonstration 1 :
Une première possibilité consiste à utiliser la Propriété 1. En effet, pour tout réel \(x\) : \[ \begin{align*} \exp(x)&=\exp \left(\frac{x}{2}+\frac{x}{2}\right) \\ &=\exp \left(\frac{x}{2}\right) \times \exp \left(\frac{x}{2}\right)\text{ (d'après la Propriété 1)} \\ &=\left(\exp \left(\frac{x}{2}\right)\right)^{2} \\ &\geq 0, \end{align*} \] car le carré d'un réel est positif.
D'après la démonstration de la Définition 1, Partie 1, nous avons \(\exp(x)\neq 0\). Par conséquent, nous avons bien \(\exp(x)>0\) pour tout réel \(x\).
Démonstration 2
La fonction \(\exp\) est continue sur \(\mathbb{R}\) (car dérivable sur \(\mathbb{R}\)), et \(\exp(0)=1\).
Imaginons que la fonction exponentielle prenne une valeur strictement négative en un certain réel \(x\), alors d'après le théorème des valeurs intermédiaires, il existe au moins un réel \(\alpha\) tel que \(\exp(\alpha)=0\).
Or nous avons vu dans la démonstration de l'unicité de la fonction exponentielle (Définition 1, Partie 1) que \(\exp(x)\neq 0\) pour tout réel \(x\).
Par conséquent, il est impossible que la fonction exponentielle prenne une valeur strictement négative en un certain réel \(x\).
Nous avons bien \(\exp(x) > 0\) pour tout réel \(x\).
Une première possibilité consiste à utiliser la Propriété 1. En effet, pour tout réel \(x\) : \[ \begin{align*} \exp(x)&=\exp \left(\frac{x}{2}+\frac{x}{2}\right) \\ &=\exp \left(\frac{x}{2}\right) \times \exp \left(\frac{x}{2}\right)\text{ (d'après la Propriété 1)} \\ &=\left(\exp \left(\frac{x}{2}\right)\right)^{2} \\ &\geq 0, \end{align*} \] car le carré d'un réel est positif.
D'après la démonstration de la Définition 1, Partie 1, nous avons \(\exp(x)\neq 0\). Par conséquent, nous avons bien \(\exp(x)>0\) pour tout réel \(x\).
Démonstration 2
La fonction \(\exp\) est continue sur \(\mathbb{R}\) (car dérivable sur \(\mathbb{R}\)), et \(\exp(0)=1\).
Imaginons que la fonction exponentielle prenne une valeur strictement négative en un certain réel \(x\), alors d'après le théorème des valeurs intermédiaires, il existe au moins un réel \(\alpha\) tel que \(\exp(\alpha)=0\).
Or nous avons vu dans la démonstration de l'unicité de la fonction exponentielle (Définition 1, Partie 1) que \(\exp(x)\neq 0\) pour tout réel \(x\).
Par conséquent, il est impossible que la fonction exponentielle prenne une valeur strictement négative en un certain réel \(x\).
Nous avons bien \(\exp(x) > 0\) pour tout réel \(x\).
Théorème 2
La fonction exponentielle est stritement croissante sur \(\mathbb{R}\).
Démonstration :
La fonction \(\exp\) est continue et dérivable sur \(\mathbb{R}\). Nous avons \[ \begin{align*} \left(\exp(x)\right)'&=\exp(x) \\ &>0, \text{ (d'après le Théorème 1),} \end{align*} \] donc la fonction exponentielle est strictement croissante sur \(\mathbb{R}\).
La fonction \(\exp\) est continue et dérivable sur \(\mathbb{R}\). Nous avons \[ \begin{align*} \left(\exp(x)\right)'&=\exp(x) \\ &>0, \text{ (d'après le Théorème 1),} \end{align*} \] donc la fonction exponentielle est strictement croissante sur \(\mathbb{R}\).
De la croissance de la fonction exponentielle, il vient immédiatement la propriété suivante.
Propriété 5
Pour tout \(a\in\mathbb{R}\) et \(b\in\mathbb{R}\) :
\[
\begin{align*}
&a < b \Leftrightarrow \exp(a) < \exp(b) \\
&a=b \Leftrightarrow \exp(a)=\exp(b).
\end{align*}
\]
Nous avons également :
Propriété 6
Pour tout \(a\in\mathbb{R}\) :
\[
\begin{align*}
&\exp(a)>1 \Leftrightarrow a>0 \\
&\exp(a)=1 \Leftrightarrow a=0 \\
&\exp(a)<1 \Leftrightarrow a<0 \\
\end{align*}
\]
Nous serons en mesure de résoudre les équations du type \(\exp(x)=a\) avec \(a\) un réel strictement positif dans le chapitre n°10.
Intéressons-nous à présent aux limites aux bornes de l'intervalle de définition de la fonction \(\exp\).
Propriété 7
\[
\begin{align*}
&\lim_{x\rightarrow +\infty}\exp(x)=+\infty
&\text{ et } \qquad
&\lim_{x\rightarrow -\infty}\exp(x)=0
\end{align*}
\]
Démonstration
Pour la première limite, nous allons démontrer que pour tout réel \(x\) positif, \(\exp(x)\geq x\).
Soit \(f\) la fonction définie sur \(\mathbb{R}+\) par \[ f(x)=\exp(x)-x \] \(f\) est dérivable sur \(\mathbb{R}+\) car c'est la somme de deux fonctions dérivables sur \(\mathbb{R}+\).
Pour tout réel \(x\) positif, nous avons : \[ f'(x)=\exp(x)-1 \] En utilisant la Propriété 6, nous avons \(f'(x)\geq 0\) pour tout \(x\) réel positif.
Par conséquent, la fonction \(f\) est croissante sur \(\mathbb{R}+\).
Nous avons donc nécessairement : \[ \begin{align*} f(x)&\geq f(0) \; \forall x\geq 0 \\ &\geq \exp(0)-0 \\ &\geq 1 \\ &> 0 \end{align*} \] Comme \(f(x)>0\) pour tout réel \(x\) strictement positif, on en déduit que \(\exp(x) > x\).
Etant donné que \(\lim_{x\rightarrow +\infty}x=+\infty\), on déduit de l'inégalité précédente que : \[ \lim_{x\rightarrow +\infty} \exp(x)=+\infty. \]
Concernant la deuxième limite : \[ \begin{align*} \lim_{x\rightarrow -\infty}\exp(x)&=\lim_{x\rightarrow +\infty}\exp(-x)\\ &=\lim_{x\rightarrow +\infty}\frac{1}{\exp(x)} \text{ (d'après la Propriété 2)}\\ &=0, \end{align*} \] car \(\lim_{x\rightarrow +\infty}\exp(x)=+\infty\) d'après la première démonstration.
Pour la première limite, nous allons démontrer que pour tout réel \(x\) positif, \(\exp(x)\geq x\).
Soit \(f\) la fonction définie sur \(\mathbb{R}+\) par \[ f(x)=\exp(x)-x \] \(f\) est dérivable sur \(\mathbb{R}+\) car c'est la somme de deux fonctions dérivables sur \(\mathbb{R}+\).
Pour tout réel \(x\) positif, nous avons : \[ f'(x)=\exp(x)-1 \] En utilisant la Propriété 6, nous avons \(f'(x)\geq 0\) pour tout \(x\) réel positif.
Par conséquent, la fonction \(f\) est croissante sur \(\mathbb{R}+\).
Nous avons donc nécessairement : \[ \begin{align*} f(x)&\geq f(0) \; \forall x\geq 0 \\ &\geq \exp(0)-0 \\ &\geq 1 \\ &> 0 \end{align*} \] Comme \(f(x)>0\) pour tout réel \(x\) strictement positif, on en déduit que \(\exp(x) > x\).
Etant donné que \(\lim_{x\rightarrow +\infty}x=+\infty\), on déduit de l'inégalité précédente que : \[ \lim_{x\rightarrow +\infty} \exp(x)=+\infty. \]
Concernant la deuxième limite : \[ \begin{align*} \lim_{x\rightarrow -\infty}\exp(x)&=\lim_{x\rightarrow +\infty}\exp(-x)\\ &=\lim_{x\rightarrow +\infty}\frac{1}{\exp(x)} \text{ (d'après la Propriété 2)}\\ &=0, \end{align*} \] car \(\lim_{x\rightarrow +\infty}\exp(x)=+\infty\) d'après la première démonstration.
Nous pouvons à présent établir le tableau de variations de la fonction \(\exp(x)\).
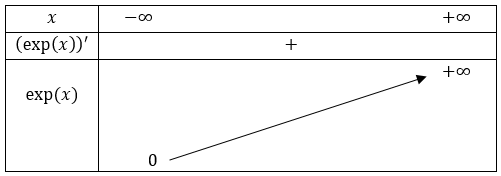
Ci-dessous nous traçons la courbe représentative de la fonction \(\exp(x)\) en bleu.
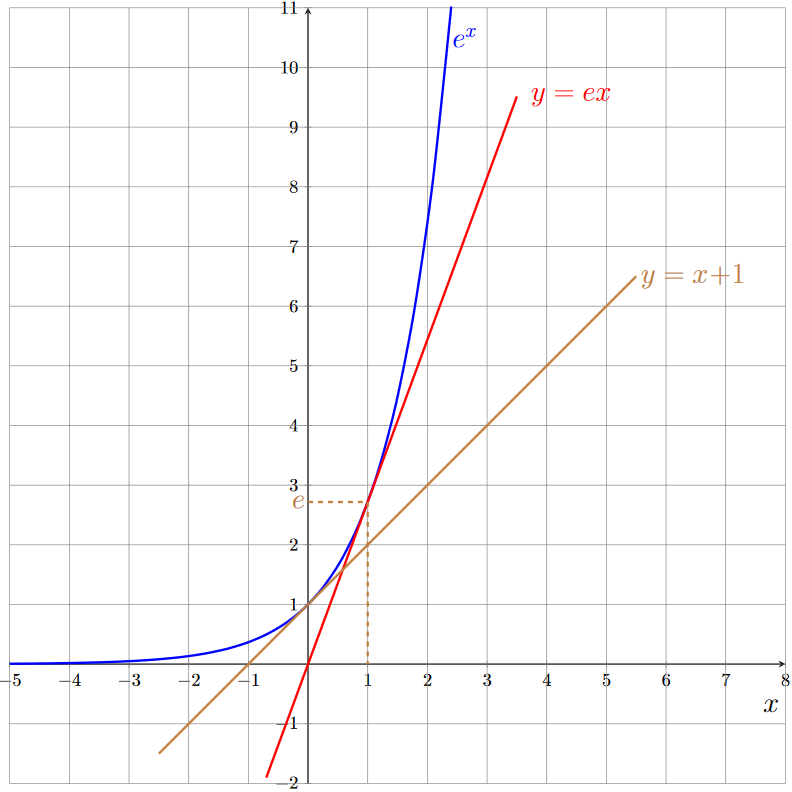
Nous avons vu précédemment que \(\lim_{x\rightarrow -\infty} \exp(x)=0\), donc l'axe des abscisses est asymptote à la courbe représentative de la fonction \(\exp\).
Nous observons bien la croissance de la fonction \(\exp\), et nous pouvons voir que \(\exp\) tend vers \(+\infty\) beaucoup plus rapidement que \(x\). Cela traduit graphiquement le Théorème 2 que nous verrons par la suite dans ce cours.
L'équation de la tangente à la courbe représentative de \(\exp\) au point \((0;1)\) est \(y=x+1\). Nous avons tracé sur le graphique la courbe représentative de cette tangente en marron.
Une autre tangente intéressante à tracer est celle au point d'abscisse 1. En effet son équation est \(y=ex\), ce qui signifie qu'elle passe par l'origine du repère. Nous avons tracé sur le graphique la courbe représentative de cette tangente en rouge.
Certains calculs de limites avec l'exponentielle peuvent poser (momentanément) problème.
Si on souhaite calculer \(\displaystyle \lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}\), on se trouve en face d'une forme indéterminée, du type \(\displaystyle \frac{+\infty}{+\infty}\).
C'est aussi le cas lorsqu'on souhaite calculer \(\lim_{x\rightarrow -\infty}x\exp(x)\) où on a une forme indéterminée du type \(-\infty\times 0\). Le théorème suivant lève l'indétermination de ces deux limites.
Théorème 2
\[
\begin{align*}
&\lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}=+\infty
&\text{ et } \qquad
&\lim_{x\rightarrow -\infty}x\exp(x)=0
\end{align*}
\]
Démonstration
Lorsque nous avons démontré la Propriété 7, nous avons établi que : \[ \exp(x)>x, \; \forall x\in \mathbb{R}+. \] En appliquant cette relation à \(\displaystyle \frac{x}{2}\), nous avons \[ \exp \left(\frac{x}{2}\right)>\left(\frac{x}{2}\right), \; \forall x\in \mathbb{R}+. \] Comme la fonction \(x\rightarrow x^{2}\) est croissante sur \(\mathbb{R}+\), nous avons : \[ \begin{align*} &\left(\exp \left(\frac{x}{2}\right)\right)^{2}>\left(\frac{x}{2}\right)^{2} \\ \Leftrightarrow & \exp \left(2\times \frac{x}{2}\right)> \frac{x^{2}}{4} \text{ (d'après la Propriété 4)} \\ \Leftrightarrow & \exp(x)> \frac{x^{2}}{4} \\ \Leftrightarrow & \frac{\exp(x)}{x}> \frac{x}{4}, \text{ car } x\in \mathbb{R}+. \end{align*} \] Etant donné que \(\displaystyle \lim_{x\rightarrow +\infty} \frac{x}{4}=0\), nous en déduisons que : \[ \lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}=+\infty. \]
soit la première limite énoncée dans le Théorème 2.
Concernant la deuxième limite : \[ \begin{align*} \lim_{x\rightarrow -\infty}x\exp(x)&=\lim_{x\rightarrow +\infty}-x\exp(-x)\\ &=\lim_{x\rightarrow +\infty}-x\frac{1}{\exp(x)}\text{ (d'après la Propriété 2)}\\ &=\lim_{x\rightarrow +\infty}-\frac{1}{\frac{\exp(x)}{x}}\\ \end{align*} \] Or nous avons vu que \(\displaystyle \lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}=+\infty\). Par conséquent : \[ \lim_{x\rightarrow -\infty}x\exp(x)=0, \] soit la deuxième limite énoncée dans le Théorème 2.
Lorsque nous avons démontré la Propriété 7, nous avons établi que : \[ \exp(x)>x, \; \forall x\in \mathbb{R}+. \] En appliquant cette relation à \(\displaystyle \frac{x}{2}\), nous avons \[ \exp \left(\frac{x}{2}\right)>\left(\frac{x}{2}\right), \; \forall x\in \mathbb{R}+. \] Comme la fonction \(x\rightarrow x^{2}\) est croissante sur \(\mathbb{R}+\), nous avons : \[ \begin{align*} &\left(\exp \left(\frac{x}{2}\right)\right)^{2}>\left(\frac{x}{2}\right)^{2} \\ \Leftrightarrow & \exp \left(2\times \frac{x}{2}\right)> \frac{x^{2}}{4} \text{ (d'après la Propriété 4)} \\ \Leftrightarrow & \exp(x)> \frac{x^{2}}{4} \\ \Leftrightarrow & \frac{\exp(x)}{x}> \frac{x}{4}, \text{ car } x\in \mathbb{R}+. \end{align*} \] Etant donné que \(\displaystyle \lim_{x\rightarrow +\infty} \frac{x}{4}=0\), nous en déduisons que : \[ \lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}=+\infty. \]
soit la première limite énoncée dans le Théorème 2.
Concernant la deuxième limite : \[ \begin{align*} \lim_{x\rightarrow -\infty}x\exp(x)&=\lim_{x\rightarrow +\infty}-x\exp(-x)\\ &=\lim_{x\rightarrow +\infty}-x\frac{1}{\exp(x)}\text{ (d'après la Propriété 2)}\\ &=\lim_{x\rightarrow +\infty}-\frac{1}{\frac{\exp(x)}{x}}\\ \end{align*} \] Or nous avons vu que \(\displaystyle \lim_{x\rightarrow +\infty}\frac{\exp(x)}{x}=+\infty\). Par conséquent : \[ \lim_{x\rightarrow -\infty}x\exp(x)=0, \] soit la deuxième limite énoncée dans le Théorème 2.
Si nous souhaitons à présent calculer \(\displaystyle \lim_{x\rightarrow 0} \frac{\exp(x)-1}{x}\), cette forme semble indéterminée, du type \(\displaystyle \frac{0}{0}\). Le Théorème suivant lève l'indétermination de cette limite.
Théorème 3
\[
\lim_{x\rightarrow 0}\frac{\exp(x)-1}{x}=1
\]
Démonstration
Nous avons : \[ \begin{align*} \lim_{x\rightarrow 0}\frac{\exp(x)-1}{x}&=\lim_{x\rightarrow 0}\frac{\exp(0+x)-\exp(0)}{x}\\ &=\exp'(0)\\ &=\exp(0) \text{ (d'après la Définition 1)} \\ &=1 \end{align*} \] En effet, on reconnaît ici le nombre dérivé de la fonction exponentielle en 0 qui vaut 1. En conclusion, nous avons bien \[ \lim_{x\rightarrow 0}\frac{\exp(x)-1}{x}=1. \]
Nous avons : \[ \begin{align*} \lim_{x\rightarrow 0}\frac{\exp(x)-1}{x}&=\lim_{x\rightarrow 0}\frac{\exp(0+x)-\exp(0)}{x}\\ &=\exp'(0)\\ &=\exp(0) \text{ (d'après la Définition 1)} \\ &=1 \end{align*} \] En effet, on reconnaît ici le nombre dérivé de la fonction exponentielle en 0 qui vaut 1. En conclusion, nous avons bien \[ \lim_{x\rightarrow 0}\frac{\exp(x)-1}{x}=1. \]
IV) Dérivées et Primitives
Dans cette section, nous allons voir comment calculer la dérivée de la fonction \(x\rightarrow \exp \left(u(x)\right)\).Le théorème de dérivation d'une fonction composée donne immédiatement le résultat, énoncé dans le Théorème 4 ci-dessous.
Théorème 4
Soit \(u\) une fonction dérivable sur un intervalle \(I\). Soit \(f\) la fonction définie par
\[
\begin{align*}
f:I&\longrightarrow \mathbb{R}^{*}_{+} \\
x&\longrightarrow \exp \left(u(x)\right)
\end{align*}
\]
La fonction \(f\) est dérivable sur \(I\) et
\[
f'(x)=u'(x)\exp \left(u(x)\right), \qquad \forall x\in I.
\]
Le théorème suivant permet de calculer les primitives de fonctions contenant des exponentielles.
Théorème 5
Soit \(u\) une fonction dérivable sur un intervalle \(I\). Les primitives sur \(\mathbb{R}\) de la fonction \(x\rightarrow u'(x)\exp\left(u(x)\right)\) sont les fonctions de la forme \(x\rightarrow \exp \left(u(x)\right)+a\), avec \(a\in \mathbb{R}\).