EXPONENTIELLE
|
Exercice 1 (Antilles-Guyane juin 2019)
Partie AD'après l'énoncé, la courbe \(\mathscr{C}_{f}\) passe par le point \(A(0; 0,5)\) donc nous avons \[ \begin{align*} &f(0)=0.5 \\ &\Longleftrightarrow \frac{a}{1+e^{-b\times 0}}=0.5 \\ &\Longleftrightarrow \frac{a}{1+e^{0}}=0.5 \\ &\Longleftrightarrow \frac{a}{1+1}=0.5 \\ &\Longleftrightarrow \frac{a}{2}=0.5 \\ &\Longleftrightarrow a=1 \end{align*} \] Nous avons alors, pour tout réel \(x\geq 0\), \[ f(x)=\frac{1}{1+e^{-bx}}. \]
2) La fonction \(f\) est dérivable sur \([0 ;+\infty[\) et pour tout réel \(x>0\), nous avons : \[ \begin{align*} &f'(x)=\frac{-1\times \left(1+e^{-bx}\right)'}{\left(1+e^{-bx}\right)^{2}}\\ &f'(x)=\frac{-\left((-b)\times e^{-bx}\right)}{\left(1+e^{-bx}\right)^{2}}\\ &f'(x)=\frac{be^{-bx}}{\left(1+e^{-bx}\right)^{2}} \end{align*} \]
3) La tangente à la courbe \(\mathscr{C}_{f}\) au point \(A (0;0.5)\) a pour équation : \[ y=f'(0)(x-0)+f(0), \] avec \( f(0)=0.5 \) et \[ \begin{align*} f'(0)&=\frac{be^{-b\times 0}}{\left(1+e^{-b\times 0}\right)^{2}}\\ &=\frac{be^{0}}{\left(1+e^{0}\right)^{2}} \\ &=\frac{b\times 1}{\left(1+1\right)^{2}} \\ &=\frac{b}{2^{2}} \\ &=\frac{b}{4}. \end{align*} \] En remplaçant dans l'équation de la tangente, cela donne : \[ y=\frac{b}{4}x+0.5. \] Nous savons que la tangente à la courbe \(\mathscr{C}_{f}\) au point \(A\) passe par le point \(B (10;1)\). Comme \(B\) appartient à cette tangente, nous avons : \[ \begin{align*} &1=\frac{b}{4}\times 10+0.5 \\ \Longleftrightarrow &1=2.5b+0.5 \\ \Longleftrightarrow &0.5=2.5b\\ \Longleftrightarrow &b=\frac{0.5}{2.5}\\ \Longleftrightarrow &b=0.2 \end{align*} \]
Partie B
1) On cherche à connaître la proportion d’individus équipés après 10 années. Elle est égale à \[ \begin{align*} p(10)&=\frac{1}{1+e^{-0.2\times 10}}\\ &=\frac{1}{1+e^{-2}}\\ &\approx 0.88 \text{ (valeur arrondie au centième)} \end{align*} \] La proportion d’individus équipés au 1er janvier 2010 est approximativement de 0.88.
2)
a) Comme la fonction \(f\) est dérivable sur \([0;+\infty[\) d'après la question 2 de la Partie A, il en est de même de la fonction \(p\) (c'est un cas particulier de la fonction \(f\) avec \(b=0.2\)).
Nous avons immédiatement pour tout \(x\) réel positif : \[ p'(x)=\frac{0.2e^{-0.2x}}{\left(1+e^{-0.2x}\right)^{2}}. \] Le démonimateur de \(p'\) étant strictement positif (le carré d'un nombre réel est toujours positif) de même que le numérateur (l'exponentielle d'un nombre est strictement positive), nous en déduisons que \(p'(x)>0\) pour tout \(x\) réel positif, ce qui signifie que \(p\) est strictement croissante sur \([0;+\infty[\).
b) Etant donné que \(\lim_{x\rightarrow +\infty}e^{-0.2x}=0\), nous pouvons conclure que \[ \lim_{x\rightarrow +\infty} p(x)=\lim_{x\rightarrow +\infty}\frac{1}{1+e^{-0.2x}}=1. \]
c) Cela signifie que lorsque la période de temps écoulé depuis le 1er janvier 2000 devient très importante, la totalité des individus possèdent l'équipement.
3) Lorsque la proportion d’individus équipés dépasse 95%, cela signifie mathématiquement que :
\[
\begin{align*}
&p(x)>0.95 \\
\Longleftrightarrow & \frac{1}{1+e^{-0.2x}} > 0.95 \\
\Longleftrightarrow & 1 > 0.95\left(1+e^{-0.2x}\right) \\
\Longleftrightarrow & 1 > 0.95+0.95e^{-0.2x} \\
\Longleftrightarrow & 0.05 > 0.95e^{-0.2x} \\
\Longleftrightarrow & \frac{0.05}{0.95} > e^{-0.2x} \\
\Longleftrightarrow & \ln \left(\frac{0.05}{0.95}\right) > -0.2x \\
\Longleftrightarrow & \frac{1}{-0.2}\ln \left(\frac{0.05}{0.95}\right) < x \\
\Longleftrightarrow & x > -5\ln \left(\frac{0.05}{0.95}\right)
\end{align*}
\]
Comme \(\displaystyle -5\ln \left(\frac{0.05}{0.95}\right) \approx 14.72\), cela signifie que c'est dans le courant de l'année 2014 (vers la fin de l'année) que le marché sera saturé.Nous avons immédiatement pour tout \(x\) réel positif : \[ p'(x)=\frac{0.2e^{-0.2x}}{\left(1+e^{-0.2x}\right)^{2}}. \] Le démonimateur de \(p'\) étant strictement positif (le carré d'un nombre réel est toujours positif) de même que le numérateur (l'exponentielle d'un nombre est strictement positive), nous en déduisons que \(p'(x)>0\) pour tout \(x\) réel positif, ce qui signifie que \(p\) est strictement croissante sur \([0;+\infty[\).
b) Etant donné que \(\lim_{x\rightarrow +\infty}e^{-0.2x}=0\), nous pouvons conclure que \[ \lim_{x\rightarrow +\infty} p(x)=\lim_{x\rightarrow +\infty}\frac{1}{1+e^{-0.2x}}=1. \]
c) Cela signifie que lorsque la période de temps écoulé depuis le 1er janvier 2000 devient très importante, la totalité des individus possèdent l'équipement.
4)
a) Pour tout réel \(x>0\) :
\[
\begin{align*}
p(x)&=\frac{1}{1+e^{-0.2x}}\\
&= \frac{1}{1+\displaystyle \frac{1}{e^{0.2x}}}\\
&=\frac{1}{\displaystyle \frac{e^{0.2x}}{e^{0.2x}}+\frac{1}{e^{0.2x}}}\\
&=\frac{1}{\displaystyle \frac{e^{0.2x}+1}{e^{0.2x}}}\\
&=\frac{e^{0.2x}}{e^{0.2x}+1}\\
&=\frac{e^{0.2x}}{1+e^{0.2x}}.
\end{align*}
\]
b) Nous avons
\[
\begin{align*}
\int p(x)dx&= \int \frac{e^{0.2x}}{1+e^{0.2x}} dx \\
&=\int \frac{0.2}{0.2}\frac{e^{0.2x}}{1+e^{0.2x}} dx \\
&=\frac{1}{0.2} \int \frac{0.2e^{0.2x}}{1+e^{0.2x}} dx \\
&=5\ln \left(1+e^{0.2x}\right)+k,
\end{align*}
\]
avec \(k\) une constante réelle.
c) Calcul de la valeur de \(m\) : \[ \begin{align*} m&=\frac{1}{2}\int_{8}^{10}p(x)dx \\ &=\frac{1}{2}\left[5\ln \left(1+e^{0.2x}\right)\right]_{8}^{10} \\ &=\frac{1}{2}\left(5 \ln \left(1+e^{0.2\times 10}\right)- 5\ln \left(1+e^{0.2\times 8}\right)\right) \\ &=2.5\left(\ln \left(1+e^{2}\right)-\ln \left(1+e^{1.6}\right)\right) \\ &=2.5 \ln\left(\frac{1+e^{2}}{1+e^{1.6}}\right) \text{ (valeur exacte)} \\ &\approx 0.86 \text{ (valeur arrondie au centième)} \end{align*} \] La proportion moyenne d'individus équipés entre 2006 et 2008 est de 0.86.
c) Calcul de la valeur de \(m\) : \[ \begin{align*} m&=\frac{1}{2}\int_{8}^{10}p(x)dx \\ &=\frac{1}{2}\left[5\ln \left(1+e^{0.2x}\right)\right]_{8}^{10} \\ &=\frac{1}{2}\left(5 \ln \left(1+e^{0.2\times 10}\right)- 5\ln \left(1+e^{0.2\times 8}\right)\right) \\ &=2.5\left(\ln \left(1+e^{2}\right)-\ln \left(1+e^{1.6}\right)\right) \\ &=2.5 \ln\left(\frac{1+e^{2}}{1+e^{1.6}}\right) \text{ (valeur exacte)} \\ &\approx 0.86 \text{ (valeur arrondie au centième)} \end{align*} \] La proportion moyenne d'individus équipés entre 2006 et 2008 est de 0.86.
Exercice 2 (Asie juin 2019 Partie B)
1)
a) D'après l'énoncé, \(\theta\) est une fonction dérivable sur l'intervalle \([0 ;+\infty[\).
D'autre part, la fonction \( t \longrightarrow e^{-0.2t}\) est dérivable sur ce même intervalle et non nulle.
Comme \(f\) est le quotient de deux fonctions dérivables sur \([0 ;+\infty[\) dont le dénominateur ne s'annule pas, alors \(f\) est dérivable sur \([0 ;+\infty[\).
Nous avons pour tout réel \(t\) positif : \[ \begin{align*} f'(t)&=\frac{\theta'(t)e^{-0.2t}-\theta(t)\times \left(-0.2e^{-0.2t}\right)}{\left(e^{-0.2t}\right)^{2}} \\ &=\frac{-0.2\theta(t) e^{-0.2t}+0.2\theta(t)e^{-0.2t}}{\left(e^{-0.2t}\right)^{2}} \\ &=0 \end{align*} \]
b) Nous avons : \[ \begin{align*} f(0)&=\frac{\theta(0)}{e^{-0.2\times 0}}\\ &=\frac{80}{e^{0}}\\ &=\frac{80}{1}\\ &=80 \end{align*} \]
D'après la question a), nous avons \(f'(t)=0\) pour tout \(t\in [0;+\infty[\) ce qui signifie que \(f\) est constante sur \([0;+\infty[\).
En particulier, \(f(t)=f(0)\) pour tout réel \(t\) positif. Or \(f(0)=80\) et nous avons par conséquent \(\forall t \in [0;+\infty[\) : \[ f(t)=80 \] et comme \[ f(t)=\frac{\theta(t)}{e^{-0.2t}}, \] nous en déduisons \(\forall t \in [0;+\infty[\) : \[ \begin{align*} \theta(t)&=f(t)e^{-0.2t}\\ &=80e^{-0.2t}. \end{align*} \]
c) Nous devons vérifier que \(\theta(0)=80\) et que \(\theta'(t)=-0.2\theta(t)\).
Nous avons d'une part : \[ \begin{align*} \theta(0)&=80e^{-0.2\times 0}\\ &=80e^{0}\\ &=80\times 1\\ &=80, \end{align*} \] et d'autre part : \[ \begin{align*} \theta'(t)&=80\times (-0.2)\times e^{-0.2t}\\ &=-0.2\times 80\times e^{-0.2t}\\ &=-0.2\theta(t). \end{align*} \] La fonction \(\theta\) trouvée en b) est bien solution du problème.
D'autre part, la fonction \( t \longrightarrow e^{-0.2t}\) est dérivable sur ce même intervalle et non nulle.
Comme \(f\) est le quotient de deux fonctions dérivables sur \([0 ;+\infty[\) dont le dénominateur ne s'annule pas, alors \(f\) est dérivable sur \([0 ;+\infty[\).
Nous avons pour tout réel \(t\) positif : \[ \begin{align*} f'(t)&=\frac{\theta'(t)e^{-0.2t}-\theta(t)\times \left(-0.2e^{-0.2t}\right)}{\left(e^{-0.2t}\right)^{2}} \\ &=\frac{-0.2\theta(t) e^{-0.2t}+0.2\theta(t)e^{-0.2t}}{\left(e^{-0.2t}\right)^{2}} \\ &=0 \end{align*} \]
b) Nous avons : \[ \begin{align*} f(0)&=\frac{\theta(0)}{e^{-0.2\times 0}}\\ &=\frac{80}{e^{0}}\\ &=\frac{80}{1}\\ &=80 \end{align*} \]
D'après la question a), nous avons \(f'(t)=0\) pour tout \(t\in [0;+\infty[\) ce qui signifie que \(f\) est constante sur \([0;+\infty[\).
En particulier, \(f(t)=f(0)\) pour tout réel \(t\) positif. Or \(f(0)=80\) et nous avons par conséquent \(\forall t \in [0;+\infty[\) : \[ f(t)=80 \] et comme \[ f(t)=\frac{\theta(t)}{e^{-0.2t}}, \] nous en déduisons \(\forall t \in [0;+\infty[\) : \[ \begin{align*} \theta(t)&=f(t)e^{-0.2t}\\ &=80e^{-0.2t}. \end{align*} \]
c) Nous devons vérifier que \(\theta(0)=80\) et que \(\theta'(t)=-0.2\theta(t)\).
Nous avons d'une part : \[ \begin{align*} \theta(0)&=80e^{-0.2\times 0}\\ &=80e^{0}\\ &=80\times 1\\ &=80, \end{align*} \] et d'autre part : \[ \begin{align*} \theta'(t)&=80\times (-0.2)\times e^{-0.2t}\\ &=-0.2\times 80\times e^{-0.2t}\\ &=-0.2\theta(t). \end{align*} \] La fonction \(\theta\) trouvée en b) est bien solution du problème.
2) La fonction \(g\) est dérivable sur \([0;+\infty[\) et de dérivée : \[ \begin{align*} g'(t)&=70\times (-0.2)\times e^{-0.2t}\\ &=-14e^{-0.2t} \end{align*} \] Nous voyons immédiatement que cette dérivée est strictement négative pour tout réel \(t\) positif, donc \(g\) est strictement décroissante sur \([0;+\infty[\).
D'autre part, nous avons \(g(0)=80>40\) et d'autre part \(\lim_{t\rightarrow +\infty}g(t)=10<40\). La fonction \(g\) étant continu et strictement décroissante sur \([0;+\infty[\), il existe un unique réel \(t_{0}\in [0;+\infty[\) tel que \(g(t_{0})=40\) d'après le théorème des valeurs intermédiaires.
Pour déterminer la valeur de \(t_{0}\), nous devons résoudre l'équation suivante : \[ \begin{align*} &g(t_{0})=40\\ \Longleftrightarrow & 10+70e^{-0.2t_{0}}=40 \\ \Longleftrightarrow & 70e^{-0.2t_{0}}=30 \\ \Longleftrightarrow & e^{-0.2t_{0}}=\frac{30}{70} \\ \Longleftrightarrow & e^{-0.2t_{0}}=\frac{3}{7} \\ \Longleftrightarrow & -0.2t_{0}=\ln\left(\frac{3}{7}\right) \\ \Longleftrightarrow & t_{0}=\frac{1}{-0.2}\ln\left(\frac{3}{7}\right) \\ \Longleftrightarrow & t_{0}=-5\ln\left(\frac{3}{7}\right) \text{ min} \\ \Longleftrightarrow & t_{0}=-5\ln\left(\frac{3}{7}\right)\times 60 \text{ s} \\ \Longleftrightarrow & t_{0}\approx 254 \text{ s} \\ \end{align*} \] Il faudra attendre environ 254 secondes, soit 4 minutes et 14 secondes, pour que le café soit à 40 degrés.
Exercice 3 (Métropole-La Réunion juin 2019)
Partie A1)
a) Nous avons \(\lim_{x\rightarrow +\infty}e^{x}=+\infty\) et \(\lim_{x\rightarrow +\infty}e^{-x}=\lim_{x\rightarrow +\infty}\displaystyle \frac{1}{e^{x}}=0\).
Par conséquent, nous avons \(\lim_{x\rightarrow +\infty}\left(e^{x}+e^{-x}\right)=+\infty\) donc \(\lim_{x\rightarrow +\infty}-\displaystyle \frac{1}{2}\left(e^{x}+e^{-x}\right)=-\infty\).
Finalement : \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \]
b) La fonction \(f\) est dérivable sur \([0 ;+\infty[\) car c'est la somme de fonctions dérivables sur ce même intervalle.
Pour tout réel \(x\) positif, nous avons : \[ f'(x)=-\frac{1}{2}\left(e^{x}-e^{-x}\right) \] Pour tout \(x\) réel strictement positif, nous avons \(-x < x \). Par croissance de la fonction exponentielle, nous avons \(e^{-x} < e^{x}\), donc \(e^{x}-e^{-x}>0\). Par conséquent, \(f'\) est strictement négative \(]0;+\infty[\) et nulle uniquement en 0 donc la fonction \(f\) est décroissante sur \([0;+\infty[\).
c) La fonction \(f\) est continue et strictement décroissante sur \([0;+\infty[\) d'après la question 1b).
De plus, \(f(0)=\displaystyle \frac{7}{2}-\frac{1}{2}\left(e^{0}+e^{-0}\right)=\frac{5}{2}>0\), et \(\lim_{x\rightarrow +\infty}f(x)=-\infty<0\) d'après la question 1a).
D'après le théorème des valeurs intermédiaires, il existe une unique valeur \(\alpha\in [0;+\infty[\) telle que \(f(x)=0\).
2) Nous avons :
\[
\begin{align*}
f(-x)&=\frac{7}{2}-\frac{1}{2}\left(e^{-x}+e^{-(-x)}\right)\\
&=\frac{7}{2}-\frac{1}{2}\left(e^{-x}+e^{x}\right)\\
&=\frac{7}{2}-\frac{1}{2}\left(e^{x}+e^{-x}\right)\\
&=f(x)
\end{align*}
\]
Comme \(f(x)=f(-x)\), étant donné que \(f(\alpha)=0\), nous avons \(f(-\alpha)=0\). Par conséquent, nous avons \(\lim_{x\rightarrow +\infty}\left(e^{x}+e^{-x}\right)=+\infty\) donc \(\lim_{x\rightarrow +\infty}-\displaystyle \frac{1}{2}\left(e^{x}+e^{-x}\right)=-\infty\).
Finalement : \[ \lim_{x\rightarrow +\infty} f(x)=-\infty. \]
b) La fonction \(f\) est dérivable sur \([0 ;+\infty[\) car c'est la somme de fonctions dérivables sur ce même intervalle.
Pour tout réel \(x\) positif, nous avons : \[ f'(x)=-\frac{1}{2}\left(e^{x}-e^{-x}\right) \] Pour tout \(x\) réel strictement positif, nous avons \(-x < x \). Par croissance de la fonction exponentielle, nous avons \(e^{-x} < e^{x}\), donc \(e^{x}-e^{-x}>0\). Par conséquent, \(f'\) est strictement négative \(]0;+\infty[\) et nulle uniquement en 0 donc la fonction \(f\) est décroissante sur \([0;+\infty[\).
c) La fonction \(f\) est continue et strictement décroissante sur \([0;+\infty[\) d'après la question 1b).
De plus, \(f(0)=\displaystyle \frac{7}{2}-\frac{1}{2}\left(e^{0}+e^{-0}\right)=\frac{5}{2}>0\), et \(\lim_{x\rightarrow +\infty}f(x)=-\infty<0\) d'après la question 1a).
D'après le théorème des valeurs intermédiaires, il existe une unique valeur \(\alpha\in [0;+\infty[\) telle que \(f(x)=0\).
Etant donné qu'\(\alpha\) est l'unique valeur annulant la fonction \(f\) sur \([0;+\infty[\), \(-\alpha\) est l'unique valeur annulant la fonction \(f\) sur \(]-\infty;0]\).
Par conséquent l'équation \(f(x)=0\) admet deux solutions dans \(\mathbb{R}\) qui sont opposées.
Partie B

1) La fonction \(f\) étant strictement décroissante sur \([0;\alpha[\), elle est strictement croissante sur \(]-\alpha;0]\) étant donné que \(f\) est paire.
Par conséquent, \(f\) admet son maximum en 0, qui vaut \(f(0)=\displaystyle \frac{5}{2}=2.5\).
\(f\) admet son minimum en \(-\alpha\) et en \(\alpha\), avec \(f(\alpha)=f(-\alpha)=0\).
Par conséquent, la hauteur d'un arceau est de 2.5 mètres.
2)
a) Nous avons pour tout réel \(x\) :
\[
\begin{align*}
1+\left(f'(x)\right)^{2}&=1+\left(-\frac{1}{2}\left(e^{x}-e^{-x}\right)\right)^{2}\\
&=1+\left(-\frac{1}{2}\right)^{2}\times \left(e^{x}-e^{-x}\right)^{2} \\
&=1+\frac{1}{4}\left(e^{2x}-2e^{x}e^{-x}+e^{-2x}\right) \\
&=\frac{4}{4}+\frac{1}{4}\left(e^{2x}-2+e^{-2x}\right) \\
&=\frac{1}{4}\left(4+e^{2x}-2+e^{-2x}\right) \\
&=\frac{1}{4}\left(e^{2x}+2+e^{-2x}\right) \\
&=\frac{1}{4}\left(e^{x}+e^{-x}\right)^{2}
\end{align*}
\]
b) Calcul de l'intégrale \(I\) :
\[
\begin{align*}
I&=\int_{0}^{\alpha}\sqrt{1+\left(f'(x)\right)^{2}}dx\\
&=\int_{0}^{\alpha}\sqrt{\frac{1}{4}\times \left(e^{x}+e^{-x}\right)^{2}}dx\text{ (d'après 2a))} \\
&=\int_{0}^{\alpha}\sqrt{\frac{1}{4}}\times \sqrt{\left(e^{x}+e^{-x}\right)^{2}}dx \\
&=\int_{0}^{\alpha}\frac{1}{2}\times \left(e^{x}+e^{-x}\right)dx\text{ car } e^{x}+e^{-x}>0 \\
&=\frac{1}{2}\int_{0}^{\alpha}e^{x}+e^{-x} dx \\
&=\frac{1}{2}\left[e^{x}-e^{-x}\right]_{0}^{\alpha} \\
&=\frac{1}{2} \left(\left(e^{\alpha}-e^{-\alpha}\right)-\left(e^{0}-e^{-0}\right)\right) \\
&=\frac{1}{2} \left(\left(e^{\alpha}-e^{-\alpha}\right)-\left(1-1\right)\right)\\
&=\frac{1}{2} \left(e^{\alpha}-e^{-\alpha}\right)
\end{align*}
\]
La longueur de la courbe \(\mathscr{C}\) sur l'intervalle \([0;\alpha]\) vaut \(I\).
Par symétrie (\(f\) étant paire), la longueur de la courbe \(\mathscr{C}\) entre \([-\alpha;0]\) vaut également \(I\).
On en conclut que la longueur d'un arceau est \(2I\), soit \(e^{\alpha}-e^{-\alpha}\).
Par symétrie (\(f\) étant paire), la longueur de la courbe \(\mathscr{C}\) entre \([-\alpha;0]\) vaut également \(I\).
On en conclut que la longueur d'un arceau est \(2I\), soit \(e^{\alpha}-e^{-\alpha}\).
Partie C
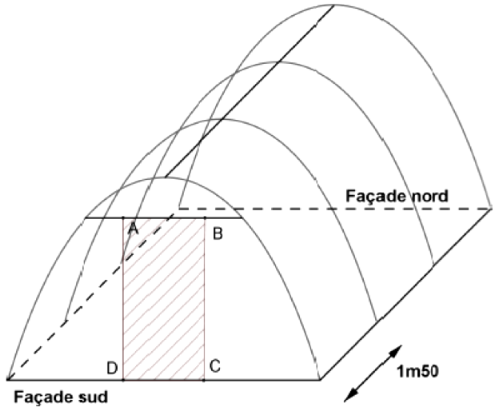
1) L'aire à calculer correspond à l'aire des deux façades à laquelle on retire l'aire du rectangle ABCD qui est de 2m2.
L'aire de chaque façade hors ouverture correspond à l'aire comprise entre la courbe représentative de la fonction \(f\), l'axe des abscisses, et les droites d'équation \(x=\alpha\) et \(x=-\alpha\).
Nous avons ainsi : \[ \begin{align*} \mathscr{A}&=2\int_{-\alpha}^{\alpha} f(x) dx-2 \\ &=2\left(\int_{-\alpha}^{0} f(x)dx+\int_{0}^{\alpha} f(x)dx\right) dx-2\\ &\text{ (d'après la relation de Chasles)} \\ &=2\times 2\int_{0}^{\alpha} f(x)dx-2 \text{ (car }f\text{ est paire)} \\ &=4\int_{0}^{\alpha}f(x)dx-2 \end{align*} \]
2) Calculons \(\mathscr{A}\) : \[ \begin{align*} \mathscr{A}&=4\int_{0}^{\alpha}f(x)dx-2\\ &=4\int_{0}^{\alpha}\left(\frac{7}{2}-\frac{1}{2}\left(e^{x}+e^{-x}\right)\right)dx-2\\ &=4\left[\frac{7}{2}x-\frac{1}{2}\left(e^{x}-e^{-x}\right)\right]_{0}^{\alpha}-2\\ &=4\left(\frac{7}{2}\alpha-\frac{1}{2}\left(e^{\alpha}-e^{-\alpha}\right)\right)-2 \\ &=14\alpha-2\left(e^{\alpha}-e^{-\alpha}\right)-2 \end{align*} \] L'aire du toit de la serre correspond à l'aire d'un rectangle, avec pour dimensions 4.5 mètres et \(2I\) (la longueur calculée dans la partie B).
L'aire totale de la bâche plastique nécessaire pour réaliser cette serre est égale à l'aire \(\mathscr{A}\) à laquelle on rajoute l'aire du toit, soit : \[ \begin{align*} \text{Aire}&=\mathscr{A}+4.5\times 2I\\ &=14\alpha-2\left(e^{\alpha}-e^{-\alpha}\right)-2+4.5\left(e^{\alpha}-e^{-\alpha}\right) \\ &=14\alpha+2.5\left(e^{\alpha}-e^{-\alpha}\right)-2\text{ (valeur exacte)}\\ &\approx 42\text{ m}^{2} \end{align*} \] Il faudra environ 42 m2 pour réaliser cette serre.
Exercice 4 (Amérique du Sud Novembre 2019)
1)
a) Nous avons
\[
\begin{align*}
f(0)&=3\times 0 \times e^{-\frac{1}{4}\times 0}+2 \\
&=2
\end{align*}
\]
Le taux de vasopressine dans le sang à l'instant \(t=0\) est de 2μg/mL.
b) Nous avons 12s = 0.2 min, donc : \[ \begin{align*} f(0.2)&=3\times 0.2 \times e^{-\frac{1}{4}\times 0.2}+2 \\ &=0.6e^{-0.05}+2\\ &\approx 2.57 \end{align*} \] Après 12 secondes, le taux de vasopressine dans le sang est de 2.57μg/mL, ce qui est au-dessus de 2.5μg/mL.
Par conséquent, le taux de vasopressine n'est pas normal.
c) Nous pouvons réécrire \(f\) de la façon suivante : \[ \begin{align*} f(t)&=3te^{-\frac{1}{4}t}+2 \\ &=3\times 4 \times \frac{1}{4}te^{-\frac{1}{4}t}+2 \\ &=12\times\left(\frac{1}{4}\right)te^{-\frac{1}{4}t}+2 \\ &=12\times\frac{\frac{1}{4}t}{e^{\frac{1}{4}t}}+2 \end{align*} \] Comme \[ \lim_{t\rightarrow +\infty}\frac{\frac{1}{4}t}{e^{\frac{1}{4}t}}=\lim_{T\rightarrow +\infty}\frac{T}{e^{T}}=0, \] nous avons finalement : \[ \lim_{t\rightarrow +\infty}f(t)=2. \] Le taux de vasopressine de stabilise à terme à 2μg/mL.
2) \(f\) est dérivable sur \([0 ;+\infty[\), et pour tout réel \(t\) positif, nous avons :
\[
\begin{align*}
f'(t)&=3\left(1\times e^{-\frac{1}{4}t}+t\times \left(-\frac{1}{4}\right)e^{-\frac{1}{4}t}\right)\\
&=3\left(e^{-\frac{1}{4}t}-\frac{1}{4}te^{-\frac{1}{4}t}\right)\\
&=3e^{-\frac{1}{4}t}\left(1-\frac{1}{4}t\right)\\
&=\frac{3}{4}(4-t)e^{-\frac{1}{4}t}.
\end{align*}
\]
3)
b) Nous avons 12s = 0.2 min, donc : \[ \begin{align*} f(0.2)&=3\times 0.2 \times e^{-\frac{1}{4}\times 0.2}+2 \\ &=0.6e^{-0.05}+2\\ &\approx 2.57 \end{align*} \] Après 12 secondes, le taux de vasopressine dans le sang est de 2.57μg/mL, ce qui est au-dessus de 2.5μg/mL.
Par conséquent, le taux de vasopressine n'est pas normal.
c) Nous pouvons réécrire \(f\) de la façon suivante : \[ \begin{align*} f(t)&=3te^{-\frac{1}{4}t}+2 \\ &=3\times 4 \times \frac{1}{4}te^{-\frac{1}{4}t}+2 \\ &=12\times\left(\frac{1}{4}\right)te^{-\frac{1}{4}t}+2 \\ &=12\times\frac{\frac{1}{4}t}{e^{\frac{1}{4}t}}+2 \end{align*} \] Comme \[ \lim_{t\rightarrow +\infty}\frac{\frac{1}{4}t}{e^{\frac{1}{4}t}}=\lim_{T\rightarrow +\infty}\frac{T}{e^{T}}=0, \] nous avons finalement : \[ \lim_{t\rightarrow +\infty}f(t)=2. \] Le taux de vasopressine de stabilise à terme à 2μg/mL.
a) Le signe de \(f'\) est celui de \(4-t\). Nous avons \(f'>0\) lorsque \(t<4\), \(f'=0\) lorsque \(t=4\), et \(f'<0\) lorsque \(t>4\).
\(f\) est croissante sur \([0;4]\) et décroissante sur \([4;+\infty[\), et \(f(4)=\displaystyle \frac{12}{e}+2\).
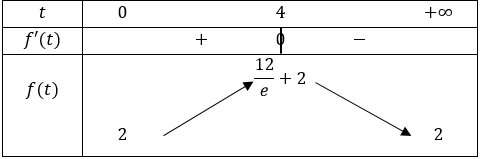
b) D'après le tableau de variations, le taux de vasopressine est maximal 4 minutes après le début de l'hémorragie. \[ \begin{align*} f(4)&=3\times 4\times e^{-\frac{1}{4}\times 4}+2\\ &=12e^{-1}+2 \\ &=\frac{12}{e}+2 \text{ (valeur exacte)} \\ &\approx 6.41 \text{ (valeur arrondie au centième)} \end{align*} \] Le taux de vasopressine est maximal au bout de 4 minutes après le début de l'hémorragie et vaut environ 6.41μg/mL.
4)
\(f\) est croissante sur \([0;4]\) et décroissante sur \([4;+\infty[\), et \(f(4)=\displaystyle \frac{12}{e}+2\).

b) D'après le tableau de variations, le taux de vasopressine est maximal 4 minutes après le début de l'hémorragie. \[ \begin{align*} f(4)&=3\times 4\times e^{-\frac{1}{4}\times 4}+2\\ &=12e^{-1}+2 \\ &=\frac{12}{e}+2 \text{ (valeur exacte)} \\ &\approx 6.41 \text{ (valeur arrondie au centième)} \end{align*} \] Le taux de vasopressine est maximal au bout de 4 minutes après le début de l'hémorragie et vaut environ 6.41μg/mL.
a) La fonction \(f\) est continue et strictement croissante sur l'intervalle \([0;4]\).
De plus, nous avons \(f(0)=2 < 2.5\), et \(f(4)\approx 6.41 > 2.5\), donc d'après le théorème des valeurs intermédiaires, il existe une unique valeur \(t_{0}\in [0;4]\) telle que \(f(t_{0})=2.5\).
En utilisant la calculatrice, nous obtenons \(t_{0}\approx 0.175\).
b) Le taux de vasopressine est supérieur à 2.5μg/mL chez une personne victime d’une hémorragie entre \(t=0.175\) et \(t=18.930\), soit pendant 18.755 minutes.
De plus, nous avons \(f(0)=2 < 2.5\), et \(f(4)\approx 6.41 > 2.5\), donc d'après le théorème des valeurs intermédiaires, il existe une unique valeur \(t_{0}\in [0;4]\) telle que \(f(t_{0})=2.5\).
En utilisant la calculatrice, nous obtenons \(t_{0}\approx 0.175\).
b) Le taux de vasopressine est supérieur à 2.5μg/mL chez une personne victime d’une hémorragie entre \(t=0.175\) et \(t=18.930\), soit pendant 18.755 minutes.
5)
a) Nous avons :
\[
\begin{align*}
F'(t)&=-12\left(e^{-\frac{1}{4}t}+(t+4)\times \left(-\frac{1}{4}\right)e^{-\frac{1}{4}t}\right)+2\\
&=3\left(-4e^{-\frac{1}{4}t}+(t+4)\times e^{-\frac{1}{4}t}\right)+2\\
&=3\left(-4e^{-\frac{1}{4}t}+t\times e^{-\frac{1}{4}t}+4e^{-\frac{1}{4}t}\right)+2\\
&=3t\times e^{-\frac{1}{4}t}+2\\
&=f(t)
\end{align*}
\]
Etant donné que \(F'(t)=f(t)\) pour tout réel \(t\) positif, nous pouvons conclure que \(F\) est une primitive de la fonction \(f\).
Nous avons : \[ \begin{align*} \int_{t_{0}}^{t_{1}}f(t)dt&=\left[F(t)\right]_{t_{0}}^{t_{1}}\\ &=-12\left(t_{1}+4\right)e^{-\frac{1}{4}t_{1}}+2t_{1}+12\left(t_{0}+4\right)e^{-\frac{1}{4}t_{0}}-2t_{0}\\ &\approx 83 \end{align*} \]
b) Le taux moyen de vasopressine lors d'un lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL est égal à : \[ \begin{align*} \frac{1}{t_{1}-t_{0}}\int_{t_{0}}^{t_{1}}f(t)dt&\approx\frac{1}{18.930-0.175}\times 83 \\ &\approx 4.4 \end{align*} \] Le taux moyen de vasopressine lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL est de 4.4μg/mL.
Nous avons : \[ \begin{align*} \int_{t_{0}}^{t_{1}}f(t)dt&=\left[F(t)\right]_{t_{0}}^{t_{1}}\\ &=-12\left(t_{1}+4\right)e^{-\frac{1}{4}t_{1}}+2t_{1}+12\left(t_{0}+4\right)e^{-\frac{1}{4}t_{0}}-2t_{0}\\ &\approx 83 \end{align*} \]
b) Le taux moyen de vasopressine lors d'un lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL est égal à : \[ \begin{align*} \frac{1}{t_{1}-t_{0}}\int_{t_{0}}^{t_{1}}f(t)dt&\approx\frac{1}{18.930-0.175}\times 83 \\ &\approx 4.4 \end{align*} \] Le taux moyen de vasopressine lors d’un accident hémorragique durant la période où ce taux est supérieur à 2,5 μg/mL est de 4.4μg/mL.
Exercice 5 (Nouvelle Calédonie février 2020)
Partie A
1) Etant donné que la courbe représentative de la fonction \(f\) coupe l'axe des ordonnées au point d'ordonnée 1, nous avons \(f(0)=1\).
Etant donné que la courbe représentative de la fonction \(f\) admet une tangente horizontale au point d'abscisse 1, cela signifie que nous avons \(f'(1)=0\).
2) La fonction \(f\) est dérivable sur \([0;+\infty[\) d'après l'énoncé. Pour tout réel \(x\) positif, nous avons : \[ \begin{align*} f'(x)&=ae^{-\frac{1}{2}x}+(ax+b)\times \left(-\frac{1}{2}\right)e^{-\frac{1}{2}x}\\ &=\left(a-\frac{1}{2}\left(ax+b\right)\right)e^{-\frac{1}{2}x} \\ &=\left(-\frac{1}{2}ax-\frac{1}{2}b+a\right)e^{-\frac{1}{2}x}. \end{align*} \]
3) Calcul de \(f(0)\) : \[ \begin{align*} f(0)&=(a\times 0+b)e^{-\frac{1}{2}\times 0} \\ &=be^{0}\\ &=b \end{align*} \] Comme \(f(0)=1\), on en déduit que \(b=1\).
D'autre part : \[ \begin{align*} f'(1)&=\left(-\frac{1}{2}a\times 1-\frac{1}{2}b+a\right)e^{-\frac{1}{2}\times 1} \\ &=\left(-\frac{1}{2}a-\frac{1}{2}b+a\right)e^{-\frac{1}{2}} \\ &=\frac{1}{2}\left(a-b\right)e^{-\frac{1}{2}} \\ \end{align*} \] Comme \(f'(1)=0\), nous avons nécessairement \(a-b=0\) (l'exponentielle étant strictement positive).
Nous avons par conséquent \(a=b\), et en utilisant le résultat précédent, \(a=b=1\).
Au final : \[ f(x)=(x+1)e^{-\frac{1}{2}x}. \]
Partie B
1)
a) Pour tout réel \(x\) positif, nous avons :
\[
\begin{align*}
f(x)&=(x+1)e^{-\frac{1}{2}x}\\
&=xe^{-\frac{1}{2}x}+e^{-\frac{1}{2}x}\\
&=\frac{x}{e^{\frac{1}{2}x}}+e^{-\frac{1}{2}x}\\
&=\frac{2\times \frac{1}{2}x}{e^{\frac{1}{2}x}}+e^{-\frac{1}{2}x}\\
&=2\left(\frac{\frac{1}{2}x}{e^{\frac{1}{2}x}}\right)+e^{-\frac{1}{2}x}.
\end{align*}
\]
b) Nous avons d'une part \(\lim_{x\rightarrow +\infty} e^{-\frac{1}{2}x}=0\), et d'autre part \[ \lim_{x\rightarrow +\infty}\frac{\frac{1}{2}x}{e^{\frac{1}{2}x}}=\lim_{X\rightarrow +\infty}\frac{X}{e^{X}}=\lim_{X\rightarrow +\infty}\frac{1}{\frac{e^{X}}{X}}=0, \] car d'après le cours \(\displaystyle \lim_{X\rightarrow +\infty}\frac{e^{X}}{X}=+\infty\).
Par conséquent : \[ \lim_{x\rightarrow +\infty}f(x)=0. \]
2) En utilisant le résultat de la question 2 de la Partie A, en prenant \(a=b=1\), nous avons :
\[
\begin{align*}
f'(x)&=\left(-\frac{1}{2}x+\frac{1}{2}\right)e^{-\frac{1}{2}x}\\
&=\frac{1}{2}\left(1-x\right)e^{-\frac{1}{2}x}.
\end{align*}
\]
Comme l'exponentielle d'un réel est strictement positive, le signe de \(f'\) est celui de \(1-x\).b) Nous avons d'une part \(\lim_{x\rightarrow +\infty} e^{-\frac{1}{2}x}=0\), et d'autre part \[ \lim_{x\rightarrow +\infty}\frac{\frac{1}{2}x}{e^{\frac{1}{2}x}}=\lim_{X\rightarrow +\infty}\frac{X}{e^{X}}=\lim_{X\rightarrow +\infty}\frac{1}{\frac{e^{X}}{X}}=0, \] car d'après le cours \(\displaystyle \lim_{X\rightarrow +\infty}\frac{e^{X}}{X}=+\infty\).
Par conséquent : \[ \lim_{x\rightarrow +\infty}f(x)=0. \]
Nous avons \(f'(x)>0\) lorsque \(0\leq x < 1\), \(f'(x)=0\) lorsque \(x=1\), et \(f'(x)>0\) lorsque \(x > 1\).
Par conséquent, \(f\) est strictement croissante sur \([0;1]\) et strictement décroissante sur \([1;+\infty[\).
D'autre part, \(\displaystyle f(1)=2e^{-\frac{1}{2}}\), nous pouvons à présent dresser le tableau de variations de la fonction \(f\).

3) Pour tout réel \(x\) appartenant à l'intervalle \([0;1]\), nous avons \(f(x)\geq 1\) donc l'équation \(f(x)=0.07\) n'admet aucune solution sur l'intervalle \([0;1]\).
La fonction \(f\) est continue et strictement décroissante sur \([1;+\infty[\). Nous avons d'une part \(f(1)=2e^{-\frac{1}{2}}>0.07\), et d'autre part \(\lim_{x\rightarrow +\infty} f(x)=0<0.07\) donc d'après le théorème des aleurs intermédiaires, il existe une unique solution sur l'intervalle \([1;+\infty[\) à l'équation \(f(x)=0.07\), que l'on note \(\alpha\).
Conclusion : L'équation \(f(x)=0.07\) admet une unique solution sur l'intervalle \([0;+\infty[\).
4) En utilisant la calculatrice, nous obtenons \(\alpha \approx 10\).
Partie C - Modélisation d'un tas de sable

1) Si le tas de sable a pour hauteur 7 cm, ou encore 0.07 mètre, cela signifie que \(f(x)=0.07\).
Or nous avons trouvé l'unique valeur de \(x\) telle que cette égalité soit vraie dans la Partie B : \(x=\alpha\approx 10\).
Par conséquent le mur de droite doit être placé à environ 10 mètres du mur de gauche.
2) Nous avons pour tout réel \(x\in [0;10]\) : \[ \begin{align*} G'(x)&=(-2x-4)'e^{-\frac{1}{2}x}+(-2x-4)\left(e^{-\frac{1}{2}x}\right)'\\ &=-2e^{-\frac{1}{2}x}+(-2x-4)\times \left(-\frac{1}{2}\right)e^{-\frac{1}{2}x} \\ &=-2e^{-\frac{1}{2}x}+xe^{-\frac{1}{2}x}+2e^{-\frac{1}{2}x} \\ &=xe^{-\frac{1}{2}x}\\ &=g(x) \end{align*} \] Comme \(G'(x)=g(x)\), alors \(G\) est une primitive de la fonction \(g\) sur l'intervalle \([0;10]\).
3) Nous avons : \[ \begin{align*} \int_{0}^{10}f(x)dx&=\int_{0}^{10}(x+1)e^{-\frac{1}{2}x}dx\\ &=\int_{0}^{10}xe^{-\frac{1}{2}x}dx+\int_{0}^{10}e^{-\frac{1}{2}x}dx\\ &=\int_{0}^{10}g(x) dx+\int_{0}^{10}e^{-\frac{1}{2}x}dx\\ &=\left[G(x)\right]_{0}^{10}+\left[-2e^{-\frac{1}{2}x}\right]_{0}^{10}\\ &=\left[G(x)-2e^{-\frac{1}{2}x}\right]_{0}^{10}\\ &=G(10)-2e^{-5}-\left(G(0)-2e^{0}\right)\\ &=G(10)-2e^{-5}-G(0)+2\\ &=(-2\times 10-4)e^{-\frac{1}{2}\times 10}-2e^{-5}-(-4)e^{0}+2 \\ &=-24e^{-5}-2e^{-5}+4+2 \\ &=6-26e^{-5} \end{align*} \]
4) Nous devons calculer la valeur moyenne de la fonction\(f\) sur l'intervalle \([0;10]\) : \[ \begin{align*} \frac{1}{10-0}\int_{0}^{10}f(x)dx&=\frac{1}{10}\times \left(6-26e^{-5}\right)\\ &\approx 0.582 m \end{align*} \] La hauteur du tas de sable une fois le nivellement réalisé sera d'environ 58 cm (valeur arrondie au cm près).