ANGLES, POLYGONES REGULIERS Correction des exercices ***

Exercice 1 (Nouvelle Calédonie décembre 2015)

1)

2) Soit A, B et C trois sommets consécutifs de ce polygone et O son centre. L'angle \(\widehat{ABC}\) qui est un angle au sommet mesure 140°. La droite (OB) est la bissectrice de l'angle \(\widehat{ABC}\), par conséquent nous avons :
\[\widehat{OBA}=\widehat{OBC}=\frac{140}{2}=70^{\circ} \] Etant donné que le triangle OBA est isocèle en O, puisque O est le centre du polygone régulier, alors les angles \(\widehat{OAB}\) et \(\widehat{OBA}\) sont égaux et nous avons :
\[\widehat{OBA}=\widehat{OAB}=70^{\circ} \] La somme des angles du triangle AOB vaut 180°, par conséquent, la mesure de l'angle \(\widehat{AOB}\) vaut :
\[ \begin{align*} \widehat{AOB}&=180-\widehat{OBA}-\widehat{OAB}\\ &=180-70-70\\
&=40^{\circ} \end{align*} \] L'angle au centre \(\widehat{AOB}\) mesure 40°.
Comme la somme des angles au centre vaut 360° et que chaque angle au centre mesure 40°, ce polygone régulier a un nombre de côtés égal à :
\[\frac{360}{40}=9 \] Ce polygone régulier a 9 côtés, il s'agit d'un ennéagone (pour la culture générale !)
Chaque côté mesurant 5 cm, le périmètre est par conséquent égal à :
\[5\times 9=45\text{ centimètres} \]

Exercice 2 (Nouvelle-Calédonie mars 2015)

1) et 2)

3) [AB] est un diamètre du cercle de centre O et D un point de ce cercle donc le triangle ABD est rectangle en D.

4) Le triangle ABD est rectangle en D donc les angles \(\widehat{ABD}\) et \(\widehat{BAD}\) sont complémentaires, c'est-à-dire que leur somme vaut 90°. On en déduit la mesure de l'angle \(\widehat{BAD}\) :
\[\widehat{BAD}=90-\widehat{ABD}=90-37=53^{\circ} \] \(\widehat{BAD}\) mesure 53°.

Exercice 3 (Métropole - Antilles - Guyane juin 2014)

1) La mesure de l'angle au centre \(\widehat{AOB}\) vaut :
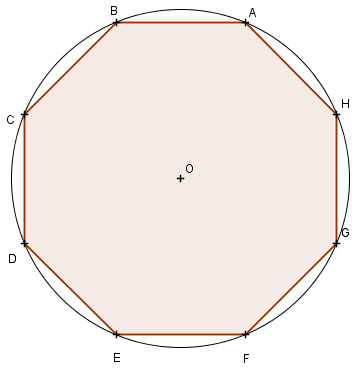
\[\widehat{AOB}=\frac{360}{8}=45^{\circ} \] Pour tracer l'octogone ABCDEFGH, on trace le segment OA tel que  OA = 3 cm. On prend le compas, pointe sèche en O et on trace le cercle de rayon OA. On prend le rapporteur et on place le point B sur ce cercle de telle sorte que l'angle \(\widehat{AOB}\) mesure 45°. On prend à nouveau le compas, on prend la distance AB et on la reporte au point B : on obtient le point C. Puis de même au point C où on reporte la distance AB : on obtient le point D. Ainsi de suite jusqu'à obtenir le point H. Il ne reste plus qu'à relier les points du cercle pour obtenir l'octogone demandé.

2) Etant donné que chaque angle au centre mesure 45°, l'angle \(\widehat{DOH}\) mesure :
\[\widehat{DOH}=4\times \widehat{AOB}=4\times 45=180^{\circ} \] Par conséquent, les points D, O et H sont alignés.
On en déduit que [DH] est un diamètre du cercle de centre O et comme A est un point de ce cercle, le triangle DAH est rectangle en A.

3) Comme chaque angle au centre mesure 45°, la mesure de l'angle \(\widehat{BOH}\) vaut :
\[\widehat{BOH}=45\times 2 = 90^{\circ} \] L'angle inscrit \(\widehat{BEH}\) intercepte le même arc de cercle \(\overset{\frown}{BH}\) que que l'angle au centre \(\widehat{BOH}\) donc nous avons\(\widehat{BOH}=2\times \widehat{BEH}\). On en déduit :
\[ \begin{align*} \widehat{BEH}&=\frac{1}{2}\times \widehat{BOH}\\ &=\frac{1}{2}\times 90\\ &=45^{\circ} \end{align*} \] \(\widehat{BEH}\) mesure 45°.

Exercice 4 (Métropole - Réunion - Mayotte juin 2009)

PARTIE 1

1) Schéma
2) E est le symétrique de B par rapport à A donc AE = AB.
On sait aussi que AB = AC donc on peut écrire les égalités suivantes :
AB = AC = AE
Le point A est donc le centre du cercle de rayon 4 cm passant par les points E, B et C.
E étant le symétrique de B par rapport à A et A le centre du cercle, [EB] est un diamètre du cercle.
En conclusion, le triangle EBC est formé par un diamètre du cercle de centre A (le côté [EB]) et un point de ce cercle (C) donc EBC est un triangle rectangle en C.

3) L’angle au centre \(\widehat{EAC}\) intercepte le même arc que l’angle inscrit \(\widehat{ABC}\) donc la mesure de l’angle \(\widehat{EAC}\) est le double de celle de l’angle \(\widehat{ABC}\).
\[\widehat{EAC}=2\times \widehat{ABC} = 2\times 43=86^{\circ} \] \(\widehat{EAC}\) mesure 86°.

Autre méthode : la somme des angles d’un triangle est égale à 180° donc
\[ \begin{align*} &\widehat{BAC}+\widehat{ACB}+\widehat{CBA}=180\\ &\widehat{BAC}=180-\widehat{ACB}-\widehat{CBA}\\ &\widehat{BAC}=180-43-43\\ &\widehat{BAC}=94^{\circ} \end{align*} \] L’angle \(\widehat{BAE}\) est plat car E est le symétrique de B par rapport à A donc :
\[ \begin{align*} &\widehat{BAC}+\widehat{EAC}=180\\ &\widehat{EAC}=180-\widehat{BAC}\\ &\widehat{EAC}=180-94\\ &\widehat{EAC}=86^{\circ} \end{align*} \] \(\widehat{EAC}\) mesure 86°.

PARTIE 2

L’angle au centre \(\widehat{EAC}\) intercepte le même arc que l’angle inscrit \(\widehat{ABC}\) donc la mesure de l’angle \(\widehat{EAC}\) est le double de celle de l’angle \(\widehat{ABC}\).
\[\widehat{EAC}=2\times \widehat{ABC} \] Jean a raison.

Correction des exercices de brevet sur les angles inscrits, angles au centre et les polygones réguliers pour la troisième (3ème)
© Planète Maths