LOGARITHME NEPERIEN
Sujet des exercices de bac S

Exercice 1 (Liban mai 2018)

On considère, pour tout entier \(n>0\), les fonctions \(f_{n}\) définies sur l’intervalle \([1 ; 5]\) par : \[ f_{n}(x)=\frac{\ln (x)}{x^{n}} \] Pour tout entier \(n>0\), on note \(\mathcal C_{n}\) la courbe représentative de la fonction \(f_{n}\) dans un repère orthogonal.
Sur le graphique ci-dessous sont représentées les courbes \(\mathcal C_{n}\) pour \(n\) appartenant à \(\{1 ; 2 ; 3 ; 4\}\).

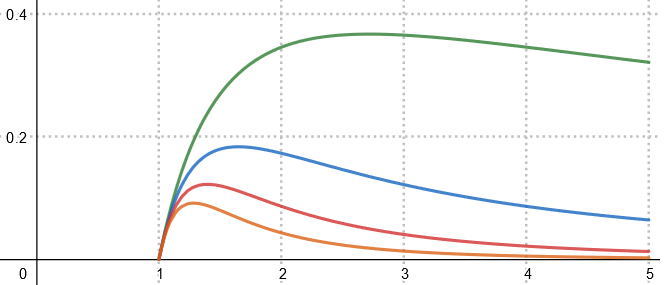
1) Montrer que, pour tout entier \(n>0\) et tout réel \(x\) de l’intervalle \([1 ; 5]\) : \[ f'_{n}(x)=\frac{1-n\ln(x)}{x^{n+1}} \] 2) Pour tout entier \(n>0\), on admet que la fonction \(f_{n}\) admet un maximum sur l’intervalle \([1 ; 5]\). On note \(A_{n}\) le point de la courbe \(\mathcal C_{n}\) ayant pour ordonnée ce maximum. Montrer que tous les points \(\mathcal A_{n}\) appartiennent à une même courbe \(\Gamma\) d’équation : \[ y=\frac{1}{e}\ln(x). \] 3)

a) Montrer que, pour tout entier \(n>1\) et tout réel \(x\) de l’intervalle \([1 ; 5]\) : \[ 0\leq \frac{\ln(x)}{x^{n}} \leq \frac{\ln(5)}{x^{n}}. \] b) Montrer que pour tout entier \(n>1\) : \[ \int_{1}^{5}\frac{1}{x^{n}}dx=\frac{1}{n-1}\left(1-\frac{1}{5^{n-1}}\right). \] c) Pour tout entier \(n>0\), on s’intéresse à l’aire, exprimée en unités d’aire, sous la courbe \(\mathcal C_{n}\), c’est-à-dire l’aire du domaine du plan délimité par les droites d’équations \(x=1\), \(x=5\), \(y=0\) et la courbe \(\mathcal C_{n}\).
Déterminer la valeur limite de cette aire quand \(n\) tend vers \(+\infty\).

Exercice 2 (Amérique du Nord mai 2018)

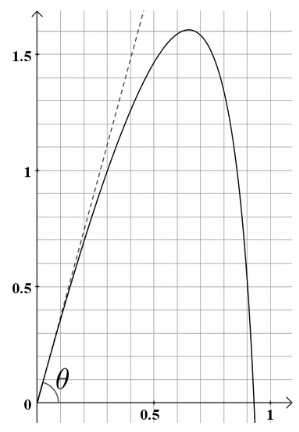Lors d’une expérience en laboratoire, on lance un projectile dans un milieu fluide. L’objectif est de déterminer pour quel angle de tir \(\theta\) par rapport à l’horizontale la hauteur du projectile ne dépasse pas 1,6 mètre.
Comme le projectile ne se déplace pas dans l’air mais dans un fluide, le modèle parabolique usuel n’est pas adopté.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction \(f\) définie sur l’intervalle \([0 ; 1[\) par : \[f(x)=bx+2\ln(1-x)\] où \(b\) est un paramètre réel supérieur ou égal à 2, \(x\) est l’abscisse du projectile, \(f(x)\) son ordonnée, toutes les deux exprimées en mètres.

1) La fonction \(f\) est dérivable sur l’intervalle \([0 ; 1[\). On note \(f'\) sa fonction dérivée.
On admet que la fonction \(f\) possède un maximum sur l’intervalle \([0 ; 1[\) et que, pour tout réel \(x\) de l’intervalle \([0 ; 1[\) : \[ f'(x)=\frac{-bx+b-2}{1-x}. \] Montrer que le maximum de la fonction \(f\) est égal à \[ b-2+2\ln \left(\frac{2}{b}\right). \] 2) Déterminer pour quelles valeurs du paramètre \(b\) la hauteur maximale du projectile ne dépasse pas 1,6 mètre.
3) Dans cette question, on choisit \(b=5.69\).
L’angle de tir \(\theta\) correspond à l’angle entre l’axe des abscisses et la tangente à la courbe de la fonction \(f\) au point d’abscisse 0 comme indiqué sur le schéma donné ci-dessus.
Déterminer une valeur approchée au dixième de degré près de l’angle \(\theta\).

Exercice 3 (Antilles-Guyane septembre 2017)

PARTIE A
Soit la fonction \(f\) définie et dérivable sur \([1 ;+\infty[\) telle que, pour tout nombre réel \(x\) supérieur ou égal à 1, \[ f(x)=\frac{1}{x}\ln(x). \] On note \(\mathcal C\) la courbe représentative de \(f\) dans un repère orthonormé.

1) Démontrer que la courbe \(\mathcal C\) admet une asymptote horizontale.
2) Déterminer la fonction dérivée \(f'\) de la fonction \(f\) sur \([1 ;+\infty[\).
3) Étudier les variations de la fonction \(f\) sur \([1 ;+\infty[\).

PARTIE B
On considère la suite \((u_{n})\) définie par \[ u_{n}=\int_{1}^{2}\frac{1}{x^{n+1}}\ln(x) dx \quad \forall n\in \mathbf{N}. \] 1) Démontrer que \[ u_{0}=\frac{1}{2}\left[\ln(2)\right]^{2}. \] Interpréter graphiquement ce résultat.
2) Prouver que, pour tout entier naturel \(n\) et pour tout nombre réel \(x\) de l'intervalle \([1 ; 2]\), on a \[ 0\leq \frac{1}{x^{n+1}}\ln(x)\leq \frac{1}{x^{n+1}}\ln (2). \] 3) En déduire que, pour tout \(n\in \mathbb{N}^{*}\), on a \[ 0\leq u_{n}\leq \frac{\ln(2)}{n}\left(1-\frac{1}{2^{n}}\right). \] 4) Déterminer la limite de la suite \((u_{n})\).

Exercice 4 (Amérique du Sud Novembre 2017)

La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d’eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins 80 avec 1 litre de pâte liquide au chocolat.

Partie A : modélisation par une fonction
Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction \(f\) définie sur \(]0 ;+\infty[\) par : \[ f(x)=\frac{x^{2}-2x-2-3\ln(x)}{x}. \] La représentation graphique de la fonction \(f\) est donnée ci-dessous.

Le repère est orthogonal d’unité 2 cm en abscisses et 1 cm en ordonnées.

1) Soit \(\phi\) la fonction définie sur \(]0 ;+\infty[\) par : \[ \phi(x)=x^{2}-1+3\ln(x). \]

a) Calculer \(\phi (1)\) et la limite de \(\phi\) en 0.
b) Etudier les variations de \(\phi\) sur \(]0 ;+\infty[\).
En déduire le signe de \(\phi(x)\) selon les valeurs de \(x\).

a) Calculer les limites de \(f\) aux bornes de son ensemble de définition.
b) Montrer que sur \(]0 ;+\infty[\) : \[ f'(x)=\frac{\phi(x)}{x^{2}}. \] En déduire le tableau de variation de \(f\).
c) Prouver que l’équation \(f(x)=0\) admet une unique solution \(\alpha\) sur \(]0; 1]\).
Déterminer à la calculatrice une valeur approchée de \(\alpha\) à 10⁻² près.
On admettra que l’équation \(f(x)=0\) a également une unique solution \(\beta\) sur \([1 ;+\infty[\) avec \(\beta \approx 3.61\) à 10⁻² près.
d) Soit \(F\) la fonction définie sur \(]0 ;+\infty[\) par : \[ F(x)=\frac{1}{2}x^{2}-2x-2\ln (x)-\frac{3}{2}\left(\ln(x)\right)^{2}. \] Montrer que \(F\) est une primitive de \(f\) sur \(]0 ;+\infty[\).

Partie B : résolution du problème
Dans cette partie, les calculs seront effectués avec les valeurs approchées à 10⁻² près de \(\alpha\) et \(\beta\) de la partie A.
Pour obtenir la forme de la goutte, on considère la courbe représentative \(\mathcal C\) de la fonction \(f\) restreinte à l’intervalle \([\alpha;\beta]\) ainsi que son symétrique \(\mathcal C'\) par rapport à l’axe des abscisses.
Les deux courbes \(\mathcal C\) et \(\mathcal C'\) délimitent la face supérieure du palet. Pour des raisons esthétiques, le chocolatier aimerait que ses palets aient une épaisseur de 0,5 cm. Dans ces conditions, la contrainte de rentabilité serait-elle respectée?

Exercice 5 (Nouvelle-Calédonie novembre 2017)

On considère la fonction \(f\) définie sur \(]0 ;+\infty[\) par \[ f(x)=\frac{(\ln x)^2}{x}. \] On note \(\mathcal C\) la courbe représentative de \(f\) dans un repère orthonormé.

1) Déterminer la limite en 0 de la fonction \(f\) et interpréter graphiquement le résultat.
2)

Démontrer que, pour tout \(x\) appartenant à \(]0 ;+\infty[\), \[ f(x)=4\left(\frac{\ln(\sqrt{x})}{\sqrt{x}}\right)^{2}. \] b) En déduire que l'axe des abscisses est une asymptote à la courbe représentative de la fonction \(f\) au voisinage de \(+\infty\).

3) On admet que \(f\) est dérivable sur \(]0 ;+\infty[\) et on note \(f'\) sa fonction dérivée.

a) Démontrer que, pour tout \(x\) appartenant à \(]0 ;+\infty[\), \[ f'(x)=\frac{\ln(x)(2-\ln(x))}{x^{2}}. \] b) Étudier le signe de \(f'(x)\) selon les valeurs du nombre réel \(x\) strictement positif.
c) Calculer \(f(1)\) et \(f(e^{2})\).
On obtient alors le tableau de variations ci-dessous.