CENTRES ETRANGERS JUIN 2016
|
Exercice 1 (3 points)
1) Réponse B.Le triangle ABC est rectangle en A donc nous avons :
\[ \begin{align*} \tan{\widehat{ABC}}&=\frac{\text{côté opposé à }\widehat{ABC}}{\text{côté adjacent à }\widehat{ABC}}\\ &=\frac{AC}{AB}\\ &=\frac{7}{5} \end{align*} \] D'après la calculatrice :
\[\tan^{-1}\left(\frac{7}{5}\right)\approx 54.46^{\circ}\] \(\widehat{ABC}\) mesure approximativement 54°.
2) Réponse B.
On doit résoudre l'équation suivante :
\[ \begin{align*} &3x-2=8\\ &3x=8+2\\ &3x=10\\ &x=\frac{10}{3}\\ &x \approx 3.33 \end{align*}\] 3.33 est compris entre 3 et 4.
3) Réponse A.
\[\frac{1-(-4)}{-2+9}=\frac{1+4}{-2+9}=\frac{5}{7}\] Remarque : la réponse C est fausse car il ne s'agit que d'une valeur approchée, or il était demandé la valeur exacte.
Exercice 2 (4 points)
Affirmation 1 :Calcul du prix au bout d'un an :
\[25\times \left(1+\frac{5}{100}\right)=26.25\] A bout d'un an, le prix sera de 26€25.
Le prix au bout de deux ans est le prix au bout d'un an qui a augmenté de 5% :
\[26.25\times \left(1+\frac{5}{100}\right)=27.5625\neq 27.50\] Au bout de deux ans le prix est de 27€5625. Par conséquent, l'affirmation 1 est fausse.
Affirmation 2 :
Si une boutique utilise en moyenne 4 kg de sucre par jour, elle utilisera environ 1,46 × 106 grammes de sucre en une année.
Quantité de sucre utilisée au bout d'un an :
4 × 365 = 1 460 kilogrammes = 1 460 000 grammes = 1,46 × 106 grammes
L'affirmation 2 est vraie.
Affirmation 3 :
Transformons 12 minutes en heure(s) :
\[12\text{ min} = \frac{12}{60}\text{ heure}=0.2\text{ heure}\] Calcul de la vitesse moyenne :
\[v=\frac{d}{t}=\frac{12.5}{0.2}=62.5\text{ km/h}\] Le livreur n'a pas respecté la limitation de vitesse puisqu'il a roulé à 62.5 km/h en moyenne alors que la limite est de 50 km/h. L'affirmation 3 est donc fausse.
Exercice 3 (5 points)

1) En I2, on doit saisir une des deux formules suivantes :
=SOMME(B2:H2)
=B2+C2+D2+E2+F2+G2+H2
2) Calculer le nombre moyen de macarons vendus par jour. Arrondir le résultat à l’unité.
Nombre moyen de macarons vendus par jour :
\[\frac{324+240+...+468}{7}=\frac{2250}{7}\approx 321\] En moyenne, 321 macarons ont été vendus chaque jour.
3) On doit d'abord ranger la série par ordre croissant :
204 - 240 - 310 - 318 - 324 - 386 - 468
Il y a sept valeurs, la médiane est donc la quatrième valeur, égale à 318.
La médiane est de 318 macarons.
4) 468 - 204 = 264
Il s'agit de la différence entre la plus grande et la plus petite valeur de la série statistique ; c'est donc l'étendue de la série.
Exercice 4 (5 points)
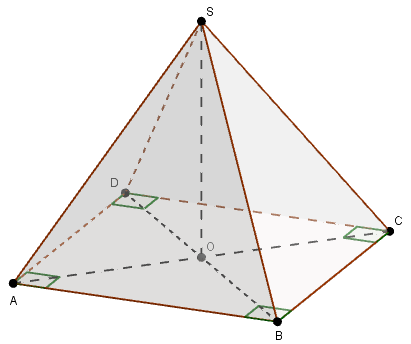
Calculons d'abord la longueur AC.
Le triangle ABC est isocèle rectangle en B donc d'après le théorème de Pythagore :
\[\begin{align*} &AC^{2}=AB^{2}+BC^{2}\\ &AC^{2}=30^{2}+30^{2}\\ &AC^{2}=900+900\\ &AC^{2}=1800\\ &AC=\sqrt{1800}\\ &AC=\sqrt{900\times 2}\\ &AC=\sqrt{900}\times \sqrt{2}\\ &AC=30\sqrt{2} \text{ valeur exacte} \end{align*}\]
Les diagonales du carré ABCD se coupent en leur milieu, donc nous avons :
\[OC=\frac{AC}{2}=\frac{30\sqrt{2}}{2}=15\sqrt{2} \]
Le triangle OCS est rectangle en O donc d'après le théorème de Pythagore :
\[\begin{align*} &OS^{2}+OC^{2}=SC^{2}\\ &OS^{2}=SC^{2}-OC^{2}\\ &OS^{2}=55^{2}-\left(15\sqrt{2}\right)^{2}\\ &OS^{2}=55^{2}-15^{2}\times (\sqrt{2})^{2}\\ &OS^{2}=55^{2}-225\times 2\\ &OS^{2}=3025-450\\ &OS^{2}=2575\\ &OS=\sqrt{2575}\\ &OS \approx 50.74\text{ cm} \end{align*}\] La hauteur de la pyramide (50.74 cm) étant supérieure à la hauteur de la vitrine (50 cm), on ne pourra pas placer ce présentoir dans la vitrine réfrigérée.
Exercice 5 (3 points)
Il y a au total deux boîtes de 12 macarons, soit 24 macarons.Soit \( x\) le nombre de macarons mangés par Pascale.
On sait qu'Alexis a mangé 4 macarons de plus que Pascale, donc Alexis en a mangé \( 4+x\).
Pascale a mangé\( x\) macarons par définition.
Pascale a mangé deux fois moins de macarons que Carole, ce qui veut dire que Carole a mangé deux fois plus de macarons que Pascale, soit \( 2x\).
Pour connaître \( x\), il nous faut résoudre l'équation suivante :
\[\begin{align*} &4+x+x+2x=24\\ &4+4x=24\\ &4x=24-4\\ &4x=20\\ &x=\frac{20}{4}\\ &x=5 \end{align*}\] \( x\) étant égal à 5 macarons, on en déduit la consommation de chaque personne :
Pascal : \( x+4=5+4=9\) macarons
Pascale : \( x=5\) macarons
Carole : \( 2x=2\times 5=10\) macarons
Exercice 6 (3 points)
1) Probabilité qu'un macaron de la boîte n°1 soit au café :\[ \begin{align*} \frac{\text{Nombre de macarons au café}}{\text{Nombre total de macarons}}&=\frac{3}{4+3+2+3}\\ &=\frac{3}{12}\\ &=0.25 \end{align*} \] La probabilité de prendre un macaron au café est de 0.25.
2) On peut représenter ce tirage sous la forme d'un arbre de probabilités :

\[\frac{2}{5}\times \frac{1}{3}=\frac{2}{15}\]
Exercice 7 (3 points)
1) Calcul du volume du cylindre :\[\begin{align*} V&=\text{Aire de la base}\times \text{hauteur}\\ &=\pi r^{2}h\\ &=\pi \times 20^{2}\times 5\\ &=\pi \times 400\times 5\\ &=2000\pi\text{ mm}^{3}\text{ valeur exacte} \end{align*}\] Le volume de crème contenu dans un macaron est 2 000\(\pi\) mm3.
2) Sachant que 1 L = 1 dm3, nous avons 30 cL = 0.30 L = 0.30 dm3 = 300 cm3 = 300 000 mm3 de crème.
Nombre de macarons qu'Alexis pourra confectionner :
\[\frac{300000}{2000\pi}\approx 47.75\] Il pourra confectionner 47 macarons avec 30 cL de crème (il ne pourra pas faire de 48ème macaron puisqu'il lui manque de la crème).
Exercice 8 (5 points)

2) Au bout de trois minutes, la température est approximativement de 70°C.
3) A la deuxième minute, la température est de 50°C. A la septième minute, la température est de 140°C. Par conséquent, la température a augmenté de 140 - 50 = 90°C entre la deuxième et la septième minute.
4) La température de 150°C est atteinte pour la première fois à la huitième minute.
5) Passé les 8 premières minutes, la température n'est pas constante à 150°C. En effet, on observe qu'elle passe au-dessus, puis en-dessous, puis à nouveau au-dessus de 150°C, ce qui explique que le responsable n'est pas satisfait de la cuisson de ses macarons.
Exercice 9 (5 points)
Lorsque le nombre de boîtes identiques commandé est supérieur à 6, Norbert a le droit à 20% de réduction. C'est le cas pour les macarons au chocolat et à la vanille. Calculons pour ces deux parfums le prix de chaque boîte après réduction.Prix d'une boîte de 12 petits macarons au chocolat ou à la vanille après réduction :
\[16\times \left(1-\frac{20}{100}\right)= 12.80€\]
Calcul du montant total commandé en macarons :
\[10\times12.80+10\times12.80+5\times16+2\times16+1\times9=377€\] Norbert a commandé pour 377€ de macarons.
Calcul des frais de livraison :
\[402-377=25€\] Norbert a payé 25€ de frais de livraison.
Etant donné qu'il s'est fait livré les macarons un samedi, l'adresse de livraison se trouve dans la zone B.