CENTRES ETRANGERS 1 JUIN 2015
Sujet du brevet

Indications portant sur l’ensemble du sujet
Les figures ou croquis ne sont pas en vraie grandeur !
Pour chaque question, laisser toutes traces de la recherche : même non aboutie, elle sera valorisée.

Exercice 1 (5,5 points)

Pour cet exercice, aucune justification n’est attendue.
En appuyant sur un bouton, on allume une des cases de la grille ci-dessous au hasard.

1	2	3
4	5	6
7	8	9

a) Quelle est la probabilité que la case 1 s’allume ?
b) Quelle est la probabilité qu’une case marquée d’un chiffre impair s’allume ?
c) Pour cette expérience aléatoire, définir un évènement qui aurait pour probabilité 1/3.

2) Les cases 1 et 7 sont restées allumées. En appuyant sur un autre bouton, quelle est la probabilité que les trois cases allumées soient alignées ?

Exercice 2 (4 points)

Le 14 octobre 2012, Félix Baumgartner, a effectué un saut d’une altitude de 38 969,3 mètres.
La première partie de son saut s’est faite en chute libre (parachute fermé). La seconde partie, s’est faite avec un parachute ouvert. Son objectif était d’être le premier homme à "dépasser le mur du son".
"Dépasser le mur du son" signifie atteindre une vitesse supérieure ou égale à la vitesse du son, c’est à dire 340 m.s⁻¹.
La Fédération Aéronautique Internationale a établi qu’il avait atteint la vitesse maximale de 1 357,6 km.h⁻¹ au cours de sa chute libre.
1) A-t-il atteint son objectif ? Justifier votre réponse.
2) Voici un tableau donnant quelques informations chiffrées sur ce saut :

Altitude du saut	38 969,3 m
Distance parcourue en chute libre	36 529 m
Durée totale du saut	9 min 3 s
Durée de la chute libre	4 min 19 s

Calculer la vitesse moyenne de Félix Baumgartner en chute avec parachute ouvert exprimée en m.s⁻¹. On arrondira à l’unité.

Exercice 3 (6 points)

Soit un cercle de diamètre [KM] avec KM = 6 cm.
Soit un point L sur le cercle tel que ML = 3 cm.
1) Faire une figure.
2) Déterminer l’aire en cm² du triangle KLM. Donner la valeur exacte puis un arrondi au cm² près.

Exercice 4 (6 points)

Mathilde et Paul saisissent sur leur calculatrice un même nombre. Voici leurs programmes de calcul :

Programme de calcul de Mathilde

• Saisir un nombre.
• Multiplier ce nombre par 9.
• Soustraire 8 au résultat obtenu.

Programme de calcul de Paul

• Saisir un nombre.
• Multiplier ce nombre par -3.
• Ajouter 31 au résultat obtenu.

1) On considère la feuille de calcul suivante :

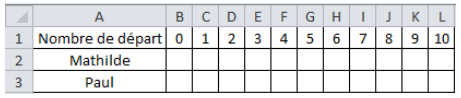
a) Quelle formule doit-on saisir dans la cellule B2 puis étirer jusqu’à la cellule L2 pour obtenir les résultats obtenus par Mathilde ?
b) Quelle formule doit-on saisir dans la cellule B3 puis étirer jusqu’à la cellule L3 pour obtenir les résultats obtenus par Paul ?

2) Voici ce que la feuille de calcul fait apparaître après avoir correctement programmé les cellules B2 et B3.

Mathilde et Paul cherchent à obtenir le même résultat. Au vu du tableau, quelle conjecture pourrait-on faire sur l’encadrement à l’unité du nombre à saisir dans les programmes pour obtenir le même résultat ?
3) Déterminer par le calcul le nombre de départ à saisir par Mathilde et Paul pour obtenir le même résultat et vérifier la conjecture sur l’encadrement.

Exercice 5 (8 points)

Il existe différentes unités de mesure de la température. En France, on utilise le degré Celsius (°C), aux États-Unis on utilise le degré Fahrenheit (°F). Voici deux représentations de cette correspondance :

1) En vous appuyant sur les représentations précédentes, déterminer s’il y a proportionnalité entre la température en degré Celsius et la température en degré Fahrenheit. Justifier votre réponse.
2) Soit \(f\) la fonction qui à une température \(x\) en degré Celsius associe la température \(f(x)\) en degré Fahrenheit correspondante. On propose trois expressions de \(f(x)\) :

Proposition 1	Proposition 2	Proposition 3
\(f(x)=x+32\)	\(f(x)=1.8x+32\)	\(f(x)=2x+30\)

"Les propositions 1 et 3 ne peuvent pas être correctes. C’est donc la proposition 2 qui convient". Justifier cette affirmation.
3) On considère la fonction \(f\) définie par \(f(x)=1.8x+32\). Calculer \(f(10)\) et \(f(-40)\).
4) Existe-t-il une valeur pour laquelle la température exprimée en degré Celsius est égale à la température exprimée en degré Fahrenheit ? Justifier votre réponse.

Exercice 6 (6,5 points)

La gélule est une forme médicamenteuse utilisée quand le médicament qu’elle contient a une odeur forte ou un goût désagréable que l’on souhaite cacher.
On trouve des gélules de différents calibres. Ces calibres sont numérotés de « 000 » à « 5 » comme le montre l’illustration ci-contre (« 000 » désignant le plus grand calibre et « 5 » désignant le plus petit) :

Le tableau suivant donne la longueur de ces différents calibres de gélule :

Calibre de la gélule	000	00	0	1	2	3	4	5
Longueur L de la gélule (en mm)	26.1	23.3	21.7	19.4	18.0	15.9	14.3	11.1

Source : « Technical Reference File 1st edition CAPSUGEL - Gélules Coni-Snap

On considère une gélule constituée de deux demi-sphères identiques de diamètre 9,5 mm et d’une partie cylindrique
d’une hauteur de 16,6 mm comme l’indique le croquis ci-dessous.

Cette représentation n’est pas en vraie grandeur.

1) À quel calibre correspond cette gélule ? Justifier votre réponse.
2) Calculer le volume arrondi au mm³ de cette gélule.
On rappelle les formules suivantes :

Volume d’un cylindre de rayon \(R\) et de hauteur \(h\) :
\[V=\pi\times R^{2}\times h\]

Volume d’un cône de rayon de base \(R\) et de hauteur \(h\) :
\[V=\frac{\pi\times R^{2}\times h}{3} \]

Volume d’une sphère de rayon \(R\) :
\[V=\frac{4}{3}\times \pi\times R^{3}\]

3) Robert tombe malade et son médecin lui prescrit comme traitement une boîte d’antibiotique conditionné en gélules correspondant au croquis ci-dessus.
Chaque gélule de cet antibiotique a une masse volumique de 6,15 × 10⁻⁴ g/mm³. La boîte d’antibiotique contient 3 plaquettes de 6 gélules.
Quelle masse d’antibiotique Robert a-t-il absorbée durant son traitement ?
Donner le résultat en grammes arrondi à l’unité.