AMERIQUE DU NORD JUIN 2015 Correction du brevet

Exercice 1 (6 points)

Questions	Réponses
1. Quelle est l'écriture scientifique de : \(\displaystyle \frac{5\times 10^{6}\times 1.2\times 10^{-8}}{2.4\times 10^{5}}\)	\(25\times 10^{-8}\)	\(2.5\times 10^{-7}\)	\(2.5\times 10^{3}\)
2. Pour \(x=20\) et \(y=5\), quelle est la valeur de R dans l'expression : \(\displaystyle \frac{1}{R}=\frac{1}{x}+\frac{1}{y}\)	0.25	4	25
3. Un article coûte 120€. Une fois soldé, il coûte 90€. Quel est le pourcentage de réduction ?	25%	30%	75%
4. On considère l’agrandissement de coefficient 2 d’un rectangle ayant pour largeur 5 cm et pour longueur 8 cm. Quelle est l’aire du rectangle obtenu ?	40 cm2	80 cm2	160 cm2

1) Réponse : \(2.5\times 10^{-7}\) \[\begin{align*} \frac{5\times 10^{6}\times 1.2\times 10^{-8}}{2.4\times 10^{5}}&=\frac{5\times 1.2\times 10^{6} \times 10^{-8}}{2.4\times 10^{5}}\\ &=\frac{6\times 10^{6+(-8)}}{2.4\times 10^{5}}\\ &=\frac{2.5\times 10^{-2}}{10^{5}}\\ &=2.5\times 10^{-2-5}\\ &=2.5\times 10^{-7} \end{align*}\]
2) Réponse : 4
\[\begin{align*} &\frac{1}{R}=\frac{1}{x}+\frac{1}{y}\\ &\frac{1}{R}=\frac{1}{20}+\frac{1}{5}\\ &\frac{1}{R}=0.05+0.2\\ &\frac{1}{R}=0.25\\ &R=\frac{1}{0.25}\\ &R=4 \end{align*}\]
3) Réponse : 25%
Montant de la réduction :
120 - 90 = 30
Le montant de la réduction est de 30€.
Calcul du pourcentage de réduction :
\[\frac{30}{120}=0.25=25\%\]
4) Réponse : 160 cm²
Si on multiplie les longueurs de ce rectangle par 2, alors on obtient un rectangle de longueur 16 cm et de largeur 10 cm. Son aire est alors égale à :
\[A=L\times l=16\times 10=160\text{ cm}^{2}\] L'aire de ce rectangle après agrandissement est de 160 cm².

Exercice 2 (4 points)

1)

2) Il n'y a pas proportionnalité entre la distance parcourue et la durée de parcours de cette étape car la représentation graphique n'est pas une droite. En effet, pour deux intervalles de temps identiques (1 heure par exemple), la distance parcourue n'est pas nécessairement la même : 30 kilomètres entre 1 heure et 2 heures, 60 kilomètres entre 2 heures et 3 heures. Le parcours était peut-être montagneux entre la première et la deuxième heure ce qui peut expliquer qu'il ait parcouru moins de kilomètres en une heure que sur d'autres créneaux horaires.

Exercice 3 (6 points)

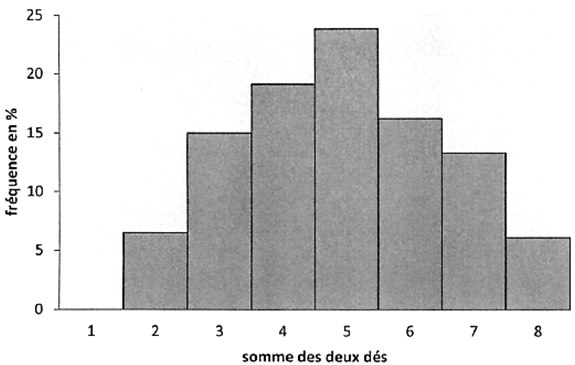
1) La fréquence d’apparition de la somme 3 est de 15% d'après le graphique.

2) La fréquence d’apparition de la somme 1 est 0%. En effet, il est impossible d'obtenir 1 en lançant deux dés où la valeur minimale de la face est 1.

3)

Exercice 4 (4 points)

Appelons \(x\) le nombre de départ.
• Je pense à un nombre : \(x\)
• Je lui soustrais 10 : \(x-10\)
• J’élève le tout au carré : \((x-10)^{2}\)
• Je soustrais au résultat le carré du nombre auquel j’ai pensé : \((x-10)^{2}-x^{2}\)
• J’obtiens alors : −340 : \((x-10)^{2}-x^{2}=-340\)
Nous devons donc résoudre l'équation suivante :
\[\begin{align*} &(x-10)^{2}-x^{2}=-340\\ &x^{2}-20x+100-x^{2}=-340\\ &-20x+100=-340\\ &100+340=20x\\ &20x=440\\ &x=\frac{440}{20}\\ &x=22 \end{align*}\] Le nombre de départ auquel je pense est 22.

Exercice 5 (4 points)

1) La phrase est "On considère que les deux hélicoptères se situent à la même altitude et que le peloton des coureurs roule sur une route horizontale."

2) Dans le triangle AMN, les points A, H et M sont alignés ainsi que les points A, L et N. De plus, les droites (HL) et (MN) sont parallèles donc d'après le théorème de Thalès :
\[\begin{align*} &\frac{AH}{AM}=\frac{AL}{AN}=\frac{HL}{MN}\\ &\frac{720}{1000}=\frac{720}{1000}=\frac{270}{MN}\\ &0.72=\frac{270}{MN}\\ \end{align*}\] On en déduit la longueur MN :
\[\begin{align*} &MN=\frac{270}{0.72}\\ &MN=375\text{ mètres} \end{align*}\] La distance MN entre les deux motos est de 375 mètres.

Exercice 6 (4 points)

Classement	NOM Prénom	Pays d'origine	Temps de course de chaque coureur
1	NIBALI Vincenzo	Italie	80 h 45 min
2	PINOT Thibaut	France	80 h 52 min
3	PERAUD Jean-Christophe	France	80 h 53 min
4	VALVERDE Alejandro	Espagne	80 h 53 min
5	BARDET Romain	France	80 h 55 min
6	VAN GARDEREN Tejay	Etats-Unis	80 h 57 min
7	MOLLEMA Bauke	Pays-Bas	80 h 59 min
8	TEN DAM Laurens	Pays-Bas	81 h 00 min
9	KONIG Leopold	République Tchèque	81 h 00 min

1) 81 h 00 min - 80 h 45 min = 15 min
15 minutes séparent Vincenzo Nibali (vainqueur) de Leopold Konig (9^ème place).

2)

Exercice 7 (8 points)

1) Calcul de la longueur AC
Etant donné que la pyramide est à base carrée, le triangle ABC est rectangle en B. On peut donc utiliser le théorème de Pythagore pour déterminer la longueur AC :
\[\begin{align*} &AB^{2}+BC^{2}=AC^{2}\\ &AC^{2}=35.5^{2}+35.5^{2}\\ &AC^{2}=1260.25+1260.25\\ &AC^{2}=2520.5\\ &AC=\sqrt{2520.5} \end{align*}\] Calcul de la longueur HC
Les diagonales d'un carré se coupant en leur milieu, H est le milieu de [AC]. On en déduit la longueur HC :
\[ \begin{align*} HC&=\frac{AC}{2}\\ &=\frac{\sqrt{2520.5}}{2}\\ &=\frac{\sqrt{2520.5}}{\sqrt{4}}\\ &=\sqrt{\frac{2520.5}{4}}\\ &=\sqrt{630.125}\text{ m} \end{align*} \] Calcul de la longueur HS
Etant donné que [HS] est la hauteur de la pyramide, le triangle HSC est rectangle en H. Connaissant les longueurs HC et CS, nous pouvons déterminer HS à l'aide du théorème de Pythagore :
\[\begin{align*} &HS^{2}+HC^{2}=SC^{2}\\ &HS^{2}=SC^{2}-HC^{2}\\ &HS^{2}=33.14^{2}-(\sqrt{630.125})^{2}\\ &HS^{2}=1098.2596-630.125\\ &HS^{2}=468.1346\\ &HS=\sqrt{468.1346}\\ &HS\approx 21.64\text{ m (arrondi au cm près)} \end{align*}\] La hauteur réelle de la pyramide du Louvre est de 21.64 mètres (valeur arrondie au cm)

2)

Correction du brevet de mathématiques Amérique du Nord 9 juin 2015 (3ème)
© Planète Maths