THEOREME DE THALES
|
I) Théorème de Thalès : Rappels (4ème)

Théorème
Soit un triangle quelconque ABC. M est un
point appartenant au segment
[AB], N un point appartenant au segment [AC] et les droites (MN) et
(BC) sont parallèles :
Alors d'après le théorème de Thalès :
\[ \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC} \]
Alors d'après le théorème de Thalès :
\[ \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC} \]
Exemple 1 : Soit un triangle ABC tel que AB = 6 cm et AC = 9 cm. M est un point du segment [AB] tel que AM = 2 cm. N est un point du segment [AC] tel que la droite (MN) est parallèle à la droite (BC). Combien mesure la longueur AN ?
Etant donné que dans le triangle ABC, les droites (MN) et (BC) sont parallèles, nous avons d'après le théorème de Thalès :
\[ \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC} \] Nous connaissons AM, AB et AC et nous cherchons la longueur AN donc nous allons nous intéresser aux rapports des longueurs suivants :
\[ \begin{align*} &\frac{AM}{AB}=\frac{AN}{AC}\\ &\frac{2}{6}=\frac{AN}{9}\\ \end{align*} \] Nous pouvons en déduire la longueur AN :
\[ \begin{align*} AN&=\frac{2}{6}\times 9\\ &=3 \text{ cm}\\ \end{align*} \] AN mesure 3 cm.
II) Nouvelle configuration de Thalès
La nouvelle configuration à laquelle on s'intéresse en troisième est celle où la droite (MN) est située "en-dehors" du triangle ABC :
Théorème
Les droites \((d)\)
et sont \((d')\)
sécantes en A. Les points M, A, B d'une part et N, A, C d'autre part
sont alignés dans le même ordre. De plus, les droites (MN) et (BC) sont
parallèles. Alors d'après le théorème de Thalès :
\[\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\]
\[\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\]
Exemple 2 : Soit deux droites (MB) et (CN) sécantes en A. On donne AB = 10 cm, AM = 5 cm et BC = 12 cm. Combien mesure la longueur MN ?
Etant donné que les points M, A, B d'une part et N, A, C d'autre part sont alignés, et que les droites (MN) et (BC) sont parallèles, nous avons d'après le théorème de Thalès :
\[\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\] Nous connaissons AB, AM et BC et nous cherchons la longueur MN donc nous allons nous intéresser aux rapports des longueurs suivants :
\[\begin{align*} &\frac{AM}{AB}=\frac{MN}{BC}\\ &\frac{5}{10}=\frac{MN}{12}\\ \end{align*} \] Nous pouvons en déduire la longueur MN :
\[ \begin{align*} MN&=\frac{5}{10}\times 12\\ &=6 \text{ cm}\\ \end{align*} \] MN mesure 6 cm.
III) Réciproque du Théorème de Thalès
La réciproque du théorème de Thalès permet de démontrer que deux droites sont parallèles.Soit la figure suivante :
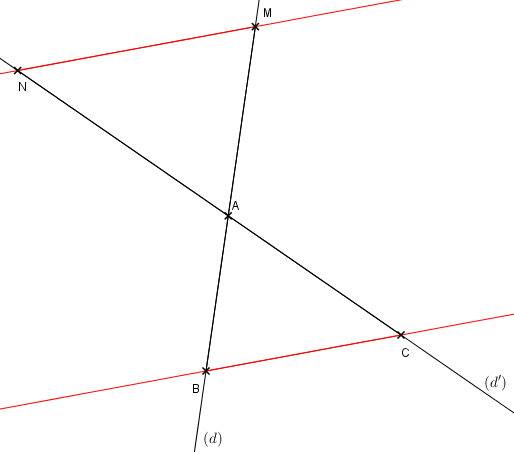
Propriété
Si les points M, A, B d'une part et N, A,
C d'autre part sont alignés dans le même ordre et si nous
avons :
\[\frac{AM}{AB}=\frac{AN}{AC}\] alors les droites (MN) et (BC) sont parallèles d'après la réciproque du théorème de Thalès.
\[\frac{AM}{AB}=\frac{AN}{AC}\] alors les droites (MN) et (BC) sont parallèles d'après la réciproque du théorème de Thalès.
Exemple 3 : Dans la figure précédente, on donne : AB = 6 cm, AM = 8 cm, AC = 9 cm, AN = 12 cm. Les droites (MN) et (BC) sont elles parallèles ?
Les points M, A, B d'une part et N, A, C d'autre part sont alignés dans le même ordre. De plus, nous avons :
\[ \frac{AM}{AB}=\frac{8}{6}=\frac{4}{3} \] Et :
\[ \frac{AN}{AC}=\frac{12}{9}=\frac{4}{3} \] Comme nous avons :
\[ \frac{AM}{AB}=\frac{AN}{AC}, \] d'après la réciproque du théorème de Thalès, les droites (MN) et (BC) sont parallèles.
Exemple 4 : Si les dimensions avaient été dans l'exemple précédent : AB = 4 cm, AM = 6 cm, AC = 5 cm, AN = 7 cm. Les droites (MN) et (BC) sont elles parallèles ?
Nous avons :
\[ \frac{AM}{AB}=\frac{6}{4}=1.5 \] Et :
\[ \frac{AN}{AC}=\frac{7}{5}=1.4 \] Comme nous avons :
\[ \frac{AM}{AB}\neq\frac{AN}{AC}, \] alors d'après la contraposée du théorème de Thalès, les droites (MN) et (BC) ne sont pas parallèles.