STATISTIQUES
|
Lorsqu'on effectue une enquête de terrain, de nombreuses
données
sont collectées, traitées et interprétées. Mais lorsqu'on souhaite les
présenter, il convient de les synthétiser, de les rendre lisibles :
imaginez que vous disposez d'une base de données sur le revenu de tous
les habitants de Paris, vous conviendrez facilement qu'il n'est pas
possible de présenter tous les chiffres. Les statistiques vont se
charger de "résumer" ces données : moyenne, médiane, et étendue sont
les premiers indicateurs de dispersion et de tendance centrale d'une
série statistique que nous allons étudier dans ce chapitre.
Celles-ci sont couramment utilisées dans tous les domaines : en démographie pour recenser les caractéristiques d'une population, en marketing pour effectuer des sondages d'opinion sur un produit, en médecine pour étudier le comportement des maladies ou des épidémies, ou encore en économie pour calculer des taux de risque.
Les statistiques permettent aussi de représenter de façon graphique un ensemble de données, ce qui permet une nouvelle fois de "simplifier" leur lecture : diagramme en bâtons, histogramme, diagramme circulaire... font partie des représentations graphiques couramment utilisées.
L'ensemble de ces éléments sont abordés dans ce cours sur les statistiques.
Celles-ci sont couramment utilisées dans tous les domaines : en démographie pour recenser les caractéristiques d'une population, en marketing pour effectuer des sondages d'opinion sur un produit, en médecine pour étudier le comportement des maladies ou des épidémies, ou encore en économie pour calculer des taux de risque.
Les statistiques permettent aussi de représenter de façon graphique un ensemble de données, ce qui permet une nouvelle fois de "simplifier" leur lecture : diagramme en bâtons, histogramme, diagramme circulaire... font partie des représentations graphiques couramment utilisées.
L'ensemble de ces éléments sont abordés dans ce cours sur les statistiques.
I) Définitions et vocabulaire
Définition
On
appelle population l'ensemble
des individus
concernés par l'étude statistique, et caractère la
propriété étudiée sur chacun d'entre eux.
Exemple 1 :
Si on réalise une enquête sur la couleur des voitures en France, l'individu statistique est une voiture et la population l'ensemble du parc automobile français. Le caractère étudié est la couleur de la voiture.
Définition
Un caractère peut être de deux types :
- quantitatif lorsqu'il est mesurable de façon numérique
- qualitatif dans les autres cas.
Les valeurs prises par les caractères sont appelées les modalités.
- quantitatif lorsqu'il est mesurable de façon numérique
- qualitatif dans les autres cas.
Les valeurs prises par les caractères sont appelées les modalités.
Exemple 2 :
Le groupe sanguin est un caractère qualitatif, dont les modalités sont "O", "A", "B", et "AB". De même pour la couleur des yeux, dont les modalités peuvent être "bleus", "bruns" ou "verts".
Le poids, la taille, les notes obtenues à un contrôle sont des caractères quantitatifs ; elles sont mesurables de façon numérique.
Définition
Un caractère quantitatif peut être discret,
c'est à dire qu'il prend un nombre fini de valeurs, ou continu, prenant
dans ce cas une infinité de valeurs.
Exemple 3 :
Les notes obtenues à un devoir de mathématiques sont un caractère quantitatif discret. En effet, elles prennent un nombre fini de valeurs comprises entre 0 et 20, par pallier de 0.25 point.
Le poids d'un cageot de fruits est un caractère quantitatif continu. Il peut prendre un nombre infini de valeurs, puisqu'il peut varier au gramme ou au milligramme près d'un cageot à l'autre. Dans ce cas, on utilisera des classes de valeur.
Définition
L'effectif
noté N est
le nombre d'individus étudiés dans l'enquête. On peut également
appeler effectif
le nombre d'individus associés à une modalité ou valeur donnée.
Exemple 4 :
Une enquête recense la couleur des yeux des élèves de quatre classes de troisième d'un collège. Les résultats sont présentés dans le tableau ci-dessous :
| Couleur des yeux | Effectif |
| Bleu | 100 |
| Brun | 40 |
| Vert | 60 |
| TOTAL | 200 |
L'effectif total est de 200 élèves. En ce qui concerne les élèves ayant les yeux bruns, l'effectif est de 40 personnes.
Définition
Pour chaque valeur prise par un caractère, on peut lui
associer sa fréquence
notée f.
C'est la proportion d'individus associés à cette valeur. En
notant 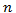 l'effectif d'une
classe ou d'une modalité et N
l'effectif total, on peut calculer la fréquence de deux façons :.
l'effectif d'une
classe ou d'une modalité et N
l'effectif total, on peut calculer la fréquence de deux façons :.
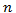 l'effectif d'une
classe ou d'une modalité et N
l'effectif total, on peut calculer la fréquence de deux façons :.
l'effectif d'une
classe ou d'une modalité et N
l'effectif total, on peut calculer la fréquence de deux façons :.- sous la forme d'un
nombre compris
entre 0 et 1 : \(\displaystyle f=\frac{n}{N}\)
- sous la forme d'un pourcentage : \(\displaystyle f=\frac{n}{N}\times 100\)
- sous la forme d'un pourcentage : \(\displaystyle f=\frac{n}{N}\times 100\)
La somme des fréquences est toujours égale à 1, ou 100 si elles sont exprimées en pourcentage.
Exemple 5 :
En reprenant le tableau présenté dans l'exercice 4, nous allons pouvoir calculer la fréquence des élèves ayant des yeux bleus, bruns ou verts :
| Couleur des yeux | Effectif | Fréquence | Fréquence (%) |
| Bleu | 100 | \(\displaystyle \frac{100}{200}=0.5\) | \(\displaystyle \frac{100}{200}\times 100=50\) |
| Brun | 40 | \(\displaystyle \frac{40}{200}=0.2\) | \(\displaystyle \frac{40}{200}\times 100=20\) |
| Vert | 60 | \(\displaystyle \frac{60}{200}=0.3\) | \(\displaystyle \frac{60}{200}\times 100=30\) |
| TOTAL | 200 | 1 | 100 |
Ainsi, la fréquence du nombre d'élèves de troisième du collège ayant les yeux bruns est de 0.2, ou 20% si on l'exprime en pourcentage.
Définition
Les effectifs
cumulés croissants s'obtiennent en additionnant l'effectif
de la modalité concernée avec ceux qui le précèdent, lorsque
les modalités sont rangées dans l'ordre croissant.
Les fréquences cumulées
croissantes s'obtiennent en divisant l'effectif cumulé
croissant par l'effectif total.
Exemple 6 :
Ci-dessous le tableau des notes obtenues par les élèves d'une classe de troisième à leur dernier contrôle de mathématiques :
| Note | 6 | 8 | 9 | 11 | 15 | 18 |
| Effectif | 4 | 5 | 4 | 3 | 2 | 2 |
Le professeur se pose la question de savoir combien d'élèves n'ont pas eu la moyenne.
Pour répondre à cette question, il va calculer les effectifs cumulés croissants :
| Note | 6 | 8 | 9 | 11 | 15 | 18 |
| Effectif | 4 | 5 | 4 | 3 | 2 | 1 |
| Effectif cumulé croissant | 4 | 9 | 13 | 16 | 18 | 20 |
Les élèves qui n'ont pas la moyenne sont ayant obtenus moins de 10 ; ils sont au nombre de 13.
Si le professeur souhaite savoir quelle est la fréquence des élèves n'ayant pas eu la moyenne, il va calculer la fréquence cumulée croissante :
\(\displaystyle \frac{13}{20}=0.65\)
(On divise l'effectif cumulé croissant, 13, par l'effectif total, 20)
Ainsi, la fréquence cumulée croissante est égale à 0.65, c'est à dire que 65% des élèves n'ont pas eu la moyenne.
II) Mesures de tendance centrale et de dispersion
A) Moyenne
Définition
Pour
un caractère
quantitatif discret, la moyenne d'une série
est égale à la somme pondérée de ses modalités, divisée par l'effectif
total.
Exemple 7 :
En reprenant l'exemple 6, la moyenne de la classe est égale à :
\[ \frac{6\times 4+8\times 5+9\times 4+11\times 3+15\times 2+18\times 2}{20}=9.95 \] La moyenne de la classe à ce contrôle est de 9.95/20.
Définition
Pour un caractère quantitatif continu, il convient de
calculer préalablement le centre de chaque classe, avant de calculer la
moyenne.
Exemple 8 :
Les salaires mensuels de l'entreprise STM qui compte 62 employés se répartissent de la façon suivante :
| Salaire | Effectif |
| [1000 ; 2000[ | 50 |
| [2000 ; 4000[ | 10 |
| [4000 ; 10000] | 2 |
On souhaiterait connaître le salaire moyen dans cette entreprise.
On détermine préalablement le centre de chaque classe pour calculer la moyenne :
| Salaire | Effectif | Centre de classe |
| [1000 ; 2000[ | 50 | 1500 |
| [2000 ; 4000[ | 10 | 3000 |
| [4000 ; 10000] | 2 | 7000 |
La moyenne est alors égale à :
\[ \frac{1500\times 50+3000\times 10+7000\times 2}{62}\approx 1919.35 \] Un salarié de l'entreprise STM gagne en moyenne 1919€35 par mois.
B) Médiane
Définition
La médiane
d'une série ordonnée
en valeurs croissantes est la valeur partageant la population étudiée
en deux sous-ensembles de même effectif.
Lorsque le caractère
quantitatif est discret, la médiane s'obtient en écrivant
successivement toutes les valeurs de la série par ordre croissant,
chacune d'entre elles étant répétée autant de fois que son effectif.
Si l'effectif total est impair, la médiane est la modalité associée à la \(\displaystyle \frac{n+1}{2}\) ème valeur de la série.
Si l'effectif total est pair, la médiane est le centre de l'intervalle formé par les modalités de la \(\displaystyle \frac{n}{2}\) ème et la \(\displaystyle \frac{n}{2}+1\)ème valeur de la série.
Si l'effectif total est impair, la médiane est la modalité associée à la \(\displaystyle \frac{n+1}{2}\) ème valeur de la série.
Si l'effectif total est pair, la médiane est le centre de l'intervalle formé par les modalités de la \(\displaystyle \frac{n}{2}\) ème et la \(\displaystyle \frac{n}{2}+1\)ème valeur de la série.
 Les valeurs de la médiane et de
la moyenne sont, en général, différentes.
Les valeurs de la médiane et de
la moyenne sont, en général, différentes.Exemple 9 :
Un garage propose 5 voitures à la vente, dont les prix en euros sont indiqués ci-dessous :
9000 7000 27000 19000 13000
Quelle est le prix médian d'une voiture ?
On réécrit tout d'abord les valeurs dans l'ordre croissant :
7000 9000 13000 19000 27000
L'effectif étant impair, la médiane est la modalité associée à la 3ème valeur de la série, c'est à dire 13000€. En effet, cette valeur partage bien l'effectif en deux groupes de même taille : 2 voitures ont un prix inférieur à 13000€, et 2 voitures ont un prix supérieur à 13000€.
Le prix médian d'une voiture est de 13000€.
Exemple 10 :
En reprenant l'exemple 6, le professeur souhaite déterminer la note médiane de la classe.
Il va tout d'abord écrire l'ensemble des notes par ordre croissant :
6 6 6 6 8 8 8 8 8 9 9 9 9 11 11 11 15 15 18 18
L'effectif total étant de 20 personnes, la médiane sera le centre de l'intervalle formé par les modalités de la 10ème et de la 11ème valeur de la série.
Ici, ces deux modalités valent 9 donc la médiane est égale à 9. Cela signifie que la moitié des élèves a eu plus de 9 tandis que l'autre moitié a obtenu une note inférieure à 9.
On peut également s'aider du tableau des effectifs cumulés croissants. Il nous indique que 9 élèves ont eu moins de 8 et que 13 élèves ont eu moins de 9. Comme on a besoin de la note obtenue par le 10ème et de la 11ème valeur pour trouver la médiane, on sait que ces deux valeurs sont égales à 9, et on obtient ainsi la médiane.
C) Etendue
Définition
L'étendue
d'une série est la différence entre la plus grande et la plus petite
valeur de la série. Il s'agit d'une mesure de dispersion de la série.
Exemple 11 :
En reprenant l'exemple 6, l'étendue est égale à la différence entre la meilleure note et la plus mauvaise :
Etendue = 18 - 6 = 12
En reprenant l'exemple 9, l'étendue est égale à la différence entre la voiture la plus chère et la moins chère :
Etendue = 27000 - 7000 = 20000
III) Représentations graphiques d'une série statistique
A) Diagramme en bâtons
Définition
Lorsque le caractère est quantitatif
et que les modalités sont discrètes,
la série statistique étudiée peut être représentée par un diagramme en bâtons,
dont la hauteur de ces derniers est proportionnelle à l'effectif ou la
fréquence associé(e) à chaque valeur.
Exemple 12 :
En reprenant l'exemple 6, les notes sont un caractère quantitatif et les valeurs sont discrètes ; la série statistique peut donc être représentée par le diagramme en bâtons ci-dessous :

B) Histogramme
Définition
Lorsque le caractère est quantitatif
et que les modalités sont continues,
la série statistique peut être représentée par un histogramme, où
l'aire de chaque rectangle est proportionnelle à l'effectif ou à la
fréquence associée à chaque classe.
On s'intéresse en 3ème uniquement aux cas où l'amplitude des classes est identique, c'est à dire que la différence entre la borne la plus élevée et la borne la plus faible de chaque intervalle est la même pour chacun d'entre-eux. Dans ce cas, la hauteur de chaque rectangle est proportionnelle à l'effectif ou à la fréquence.
Exemple 13 :
Une enquête effectuée dans un collège recense la taille des élèves. Les résultats sont reportés dans le tableau ci-dessous :
| Taille (cm) | Effectif |
| [120 ; 130[ | 5 |
| [130 ; 140[ | 15 |
| [140 ; 150[ | 40 |
| [150 ; 160[ | 50 |
| [160 ; 170[ | 30 |
| [170 ; 180] | 10 |
On constate que l'amplitude des classes est identique à chaque fois, puisqu'elle est égale à 10. On peut représenter cette série sous la forme d'un histogramme :

C) Diagramme circulaire
Définition
Lorsque le caractère est qualitatif,
la série statistique peut-être représentée par un diagramme circulaire,
dont la mesure de chaque secteur angulaire est proportionnelle à
l'effectif ou la fréquence associé(e) à la modalité. Celle-ci s'obtient
directement en multipliant la fréquence de chaque modalité par 360°.
Exemple 14 :
En reprenant l'exemple 4 avec la couleur des yeux, qui est un caractère qualitatif, déterminons tout d'abord la mesure de chaque secteur angulaire pour chaque modalité :
| Couleur des yeux | Effectif | Fréquence | Secteur angulaire (°) |
| Bleu | 100 | 0.5 | 360 × 0.5 = 180 |
| Brun | 40 | 0.2 | 360 × 0.2 = 72 |
| Vert | 60 | 0.3 | 360 × 0.3 = 108 |
| TOTAL | 200 | 1 | 360 |
Nous obtenons le diagramme circulaire suivant :
