PONDICHERY AVRIL 2015
|
Exercice 1 (5 points)
| Questions | A | B | C | |
| 1 | La forme développée de \((x-1)^{2}\) est : | \((x-1)(x+1)\) | \(x^{2}-2x+1\) | \(x^{2}+2x+1\) |
| 2 | Une solution de l'équation \(2x^{2}+3x-2=0\) est : | 0 | 2 | -2 |
| 3 | On considère la fonction \(f:x\rightarrow 3x+2\). Un antécédent de -7 par la fonction \(f\) est : | -19 | -3 | -7 |
| 4 | Lorsqu’on regarde un angle de 18° à la loupe de grossissement 2, on voit un angle de : | 9° | 36° | 18° |
| 5 | On
considère la fonction \(g:x\rightarrow
x^{2}+7\). Quelle est la formule à entrer dans la cellule B2
pour calculer \(g(-2)\) ? |
=A2^2+7 | =-22+7 | =A2*2+7 |
1) Réponse B.
\[(x-1)^{2}=x^{2}-2x+1\]
2) Réponse C.
Si on remplace \(x\) par 0 :
\[2\times 0^{2}+3\times 0-2=0+0-2=-2\neq 0\] Si on remplace \(x\) par 2 :
\[2\times 2^{2}+3\times 2-2=8+6-2=12\neq 0\] Si on remplace \(x\) par -2 :
\[2\times (-2)^{2}+3\times (-2)-2=8-6-2=0\] La bonne réponse est -2 (réponse C).
3) Réponse B.
On doit résoudre l'équation suivante :
\[\begin{align*} &3x+2=-7\\ &3x=-7-2\\ &3x=-9\\ &x=\frac{-9}{3}\\ &x=-3 \end{align*}\]
4) Réponse C (18°).
5) Réponse A (A2^2+7).
Exercice 2 (4 points)
1) Pour que tous les paquets aient la même composition et qu'il ne reste ni oeufs, ni poissons, il faut que 19 soit un diviseur de 2622 et de 2530. Nous avons :\[\frac{2622}{19}=138\] Donc 19 est un diviseur de 2622.
\[\frac{2530}{19}\approx 133.16\] Donc 19 n'est pas un diviseur de 2530.
Par conséquent, le chocolatier ne peut pas faire 19 paquets.
2) Il faut que le nombre de paquets soit un diviseur de 2622 et de 2530. Comme on veut le plus grand nombre de paquets, il faut calculer le PGCD de 2622 et de 2530. Calculons-le à l'aide de l'algorithme d'Euclide :
\[\begin{align*} &2622=2530\times 1+92\\ &2530=92\times 27+46\\ &92=46\times 2+0 \end{align*}\] Le PGCD de 2622 et 2530 est le dernier reste non nul, soit 46. Il pourra constituer 46 paquets identiques au maximum sans qu'il ne reste d'oeufs ni de poissons.
Nombre d'oeufs dans chaque paquet :
\[\frac{2622}{46}=57\] Nombre de poissons dans chaque paquet :
\[\frac{2530}{46}=55 \] Chaque paquet sera composé de 57 oeufs et 55 poissons.
Exercice 3 (6 points)
| Information 1 : les
loyers des deux emplacements proposés : • la paillotte sur la plage : 2 500€ par mois. • la boutique au centre-ville : 60€ par jour. |
| Information 2 : la
météo à Hendaye Du 1er juin au 31 août inclus : • Le soleil brille 75% du temps • Le reste du temps, le temps est nuageux ou pluvieux. |
Information 3 : prévisions des ventes par jour selon la météo :
Soleil
 |
Nuageux
- Pluvieux  |
|
| La paillotte | 500€ | 50€ |
| La boutique | 350€ | 300€ |
Nombre total de jours sur la période considérée :
30 +31 +31 = 92
Il y a 92 jours.
Nombre de jours de beau temps :
\[92\times\frac{75}{100}=69\] Il y a 69 jours de beau temps, et par conséquent 23 jours de temps nuageux ou pluvieux.
Si Peio choisit une paillotte sur la plage, alors son bénéfice sera égal à :
\[500\times 69+50\times 23-2500\times 3=28150\] Sur la plage, il réalisera un bénéfice de 28150€.
Si Peio choisit une boutique en centre-ville, alors son bénéfice sera égal à :
\[350\times 69+300\times 23-60\times 92=25530\] En centre-ville, il réalisera un bénéfice de 25530€.
Par conséquent, Peio a intérêt à choisir la paillotte sur la plage.
Exercice 4 (6 points)
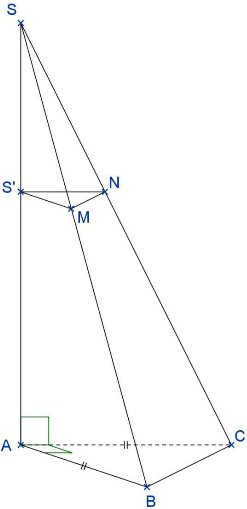
\[\begin{align*} A_{\text{ABC}}&=\frac{\text{base }\times\text{ hauteur}}{2}\\ &=\frac{AB\times AC}{2}\\ &=\frac{7.5 \times 7.5}{2}\\ &=28.125\text{ cm}^{2} \end{align*}\] L'aire de la base de la pyramide est de 28.125 cm2.
Calcul du volume de la pyramide SABC :
\[\begin{align*} V_{\text{SABC}}&=\frac{\text{Aire de la base }\times\text{ hauteur}}{3}\\ &=\frac{A_{ABC}\times AS}{3}\\ &=\frac{28.125 \times 15}{3}\\ &=140.625\text{ cm}^{3}\\ &\approx 141 \text{ cm}^{3}\text{ (valeur arrondie au cm}^{3}\text{ pr\`es)} \end{align*}\] Le volume de la pyramide SABC est de 140.625 cm3.
2)
a) La section
d'une pyramide à base triangulaire par un plan P parallèle à sa base
est un triangle.
Etant donné que le triangle ABC est isocèle rectangle en A, le triangle S'MN sera aussi isocèle rectangle en S'.
b) La pyramide SS'MN est une réduction de la pyramide SABC. Le coefficient de réduction est égal à :
\[k=\frac{SS'}{AS}=\frac{6}{15}=0.4\] Toutes les longueurs de la pyramide SABC sont multipliées par 0.4 pour obtenir celles de la pyramide SS'MN.
On en déduit la longueur S'N :
\[S'N=0.4\times AC=0.4\times 7.5=3\text{ cm}\] S'N mesure 3 cm.
Etant donné que le triangle ABC est isocèle rectangle en A, le triangle S'MN sera aussi isocèle rectangle en S'.
b) La pyramide SS'MN est une réduction de la pyramide SABC. Le coefficient de réduction est égal à :
\[k=\frac{SS'}{AS}=\frac{6}{15}=0.4\] Toutes les longueurs de la pyramide SABC sont multipliées par 0.4 pour obtenir celles de la pyramide SS'MN.
On en déduit la longueur S'N :
\[S'N=0.4\times AC=0.4\times 7.5=3\text{ cm}\] S'N mesure 3 cm.
3) Comme les dimensions de la pyramide SABC sont multipliées par 0.4 pour obtenir celles de la pyramide SS'MN, alors le volume est multiplié par 0.43 :
\[\begin{align*} V_{SS'MN}&=0.4^{3}\times V_{SABC}\\ &=0.064\times 140.625\\ &=9\text{ cm}^{3} \end{align*}\] Le volume du bouchon est de 9 cm3.
On en déduit le volume maximal de parfum que peut contenir cette bouteille :
\[\begin{align*} V_{ABCS'MN}&=V_{SABC}-V_{SS'MN}\\ &=140.625-9\\ &=131.625\text{ cm}^{3} \end{align*}\] Cette bouteille peut contenir jusqu'à 131.625 cm3 de parfum.
Exercice 5 (4 points)
1) Il y a cinq portes or une seule permet d'accéder à la salle du trésor donc la probabilité que le candidat accède à la salle du trésor est égale à :\[\frac{1}{5}=0.2\]
2)
a) Il y a 8 enveloppes
donc :
\[\begin{align*} &P(1000)=\frac{1}{8}=0.125\\ &P(200)=\frac{5}{8}=0.625\\ &P(100)=\frac{3}{8}=0.25 \end{align*}\]
b) Il peut gagner 200€ ou 1000€. La probabilité de gagner au moins 200€ est égale à :
0.625 + 0.125 = 0.75 (c'est-à-dire 3 chances sur 4).
\[\begin{align*} &P(1000)=\frac{1}{8}=0.125\\ &P(200)=\frac{5}{8}=0.625\\ &P(100)=\frac{3}{8}=0.25 \end{align*}\]

b) Il peut gagner 200€ ou 1000€. La probabilité de gagner au moins 200€ est égale à :
0.625 + 0.125 = 0.75 (c'est-à-dire 3 chances sur 4).
3) Il y a 3 enveloppes vides sur les 8 donc la probabilité de ne rien gagner est égale à :
\[\frac{3}{8}=0.375\]
Exercice 6 (7 points)
1) Figure
2)
a) VRAI
[AB] est un diamètre du cercle et C un point de ce cercle donc le triangle ABC est rectangle en C.
b) FAUX
Le triangle ABC est rectangle en C donc d'après le théorème de Pythagore :
\[\begin{align*} &AC^{2}+BC^{2}=AB^{2}\\ &BC^{2}=AB^{2}-AC^{2}\\ &BC^{2}=12^{2}-6^{2}\\ &BC^{2}=144-36\\ &BC^{2}=108\\ &BC=\sqrt{108}\\ &BC\approx 10.39\text{ cm} \end{align*}\] BC mesure environ 10.39 cm.
c) VRAI
L’angle au centre \(\widehat{AOC}\) intercepte le même arc de cercle \(\overset{\frown}{AC}\) que l'angle inscrit \(\widehat{ABC}\) donc nous avons :
\[\widehat{AOC}=2\times \widehat{ABC}=2 \times 30=60^{\circ}\] \(\widehat{AOC}\) mesure 60°.
d) VRAI
Calcul de l'aire du triangle ABC :
\[\begin{align*} A_{ABC}&=\frac{\text{Base }\times\text{ hauteur}}{2}\\ &=\frac{AC\times BC}{2}\\ &=\frac{6\times \sqrt{108}}{2}\\ &=3\sqrt{108}\\ &=3\times\sqrt{36\times3}\\ &=3\times \sqrt{36} \times \sqrt{3}\\ &=3\times 6 \times \sqrt{3}\\ &=18\sqrt{3}\text{ cm}^{2} \end{align*}\]
e) FAUX
Les angles \(\widehat{AOC}\) et \(\widehat{BOC}\) sont supplémentaires donc :
\[\begin{align*} &\widehat{AOC}+\widehat{BOC}=180\\ &\widehat{BOC}=180-\widehat{AOC}\\ &\widehat{BOC}=180-60\\ &\widehat{BOC}=120^{\circ} \end{align*}\] \(\widehat{BOC}\) mesure 120°.
[AB] est un diamètre du cercle et C un point de ce cercle donc le triangle ABC est rectangle en C.
b) FAUX
Le triangle ABC est rectangle en C donc d'après le théorème de Pythagore :
\[\begin{align*} &AC^{2}+BC^{2}=AB^{2}\\ &BC^{2}=AB^{2}-AC^{2}\\ &BC^{2}=12^{2}-6^{2}\\ &BC^{2}=144-36\\ &BC^{2}=108\\ &BC=\sqrt{108}\\ &BC\approx 10.39\text{ cm} \end{align*}\] BC mesure environ 10.39 cm.
c) VRAI
L’angle au centre \(\widehat{AOC}\) intercepte le même arc de cercle \(\overset{\frown}{AC}\) que l'angle inscrit \(\widehat{ABC}\) donc nous avons :
\[\widehat{AOC}=2\times \widehat{ABC}=2 \times 30=60^{\circ}\] \(\widehat{AOC}\) mesure 60°.
d) VRAI
Calcul de l'aire du triangle ABC :
\[\begin{align*} A_{ABC}&=\frac{\text{Base }\times\text{ hauteur}}{2}\\ &=\frac{AC\times BC}{2}\\ &=\frac{6\times \sqrt{108}}{2}\\ &=3\sqrt{108}\\ &=3\times\sqrt{36\times3}\\ &=3\times \sqrt{36} \times \sqrt{3}\\ &=3\times 6 \times \sqrt{3}\\ &=18\sqrt{3}\text{ cm}^{2} \end{align*}\]
e) FAUX
Les angles \(\widehat{AOC}\) et \(\widehat{BOC}\) sont supplémentaires donc :
\[\begin{align*} &\widehat{AOC}+\widehat{BOC}=180\\ &\widehat{BOC}=180-\widehat{AOC}\\ &\widehat{BOC}=180-60\\ &\widehat{BOC}=120^{\circ} \end{align*}\] \(\widehat{BOC}\) mesure 120°.
Exercice 7 (4 points)
Appelons \(c\) la longueur d'un côté d'un petit triangle équilatéral.Périmètre d'un petit triangle équilatéral : \(c+c+c=3c\)
Somme des périmètres des trois petits triangles équilatéraux : \(3\times 3c=9c\)
Il reste à calculer le périmètre de l'hexagone. Il a trois côtés mesurant \(c\) et trois autres côtés mesurant \(6-2c\) (longueur d'un grand triangle équilatéral auquelle on enlève deux longueurs d'un petit triangle équilatéral). Le périmètre de l'hexagone est donc égal à :
\(3c+3(6-2c)=3c+18-6c=18-3c\)
Il nous reste à résoudre l'équation suivante :
\[\begin{align*} &9c=18-3c\\ &9c+3c=18\\ &12c=18\\ &c=\frac{18}{12}\\ &c=1.5\text{ cm} \end{align*}\] Il faut que le côté des petits triangles mesure 1.5 cm pour que la somme des périmètres des trois petits triangles soit égale au périmètre de l’hexagone gris restant.
