GEOMETRIE DANS L'ESPACE, VOLUMES
Cours

I) Sphère et Boule

A) Définitions

Définition
On appelle sphère de centre \(A\) et de rayon \(r\) l'ensemble des points de l'espace situés à une distance exactement égale à \(r\) du point \(A\).
On appelle boule de centre \(A\) et de rayon \(r\) l'ensemble des points de l'espace situés à une distance inférieure ou égale à \(r\) du point \(A\).
Un grand cercle d'une sphère de centre \(A\) et de rayon \(r\) est un cercle de centre \(A\) et de rayon \(r\).

Illustration graphique

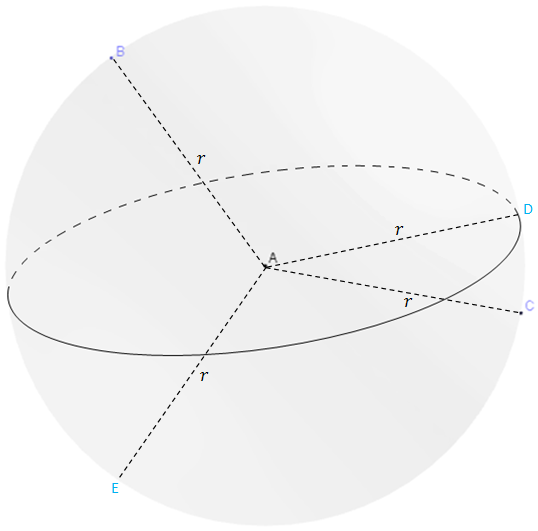
Les points \(B\), \(C\), \(D\) et \(E\) sont des points de la sphère de centre \(A\). En effet, ils sont tous situés à une distance \(r\) du centre de la sphère. Nous avons l'égalité suivante :
\(AB=AC=AD=AE=r\).
N'importe quel point \(K\) tel que \(AK \leq r\) appartient à la boule de centre \(A\).
Nous avons tracé un grand cercle de rayon \([AD]\).

Remarque
Une sphère possède une infinité de grands cercles. Un grand cercle partage la sphère en deux hémisphères.
D'autre part, la différence entre sphère et boule dans l'espace est la même qu'entre cercle et disque dans un plan.

B) Aire et volume

Propriétés
L'aire d'une sphère de rayon \(r\) est égale à :
\[ \mathcal{A}=4 \pi r^{2} \] Le volume d'une boule de rayon \(r\) est égal à :
\[V=\frac{4}{3} \pi r^{3} \]

Exemple 1 :
Calculer l'aire d'une sphère de diamètre 20 cm.
Si le diamètre est de 20 cm, alors le rayon est de 10 cm. En appliquant la formule, l'aire de la sphère est égale à :
\[ \begin{align*}
\mathcal{A}&=4\pi \times 10^{2}\\ &=400 \pi \text{ valeur exacte}\\ &\approx 1256.64 \text{ cm}^{2} \text{ valeur approchée} \end{align*} \]
Exemple 2 :
Calculer le volume d'une boule de rayon 10 cm.
En appliquant la formule, le volume de la boule est égal à :
\[ \begin{align*}
V&=\frac{4}{3}\pi \times 10^{3}\\ &=\frac{4000}{3} \pi \text{ valeur exacte}\\ &\approx 4188.79 \text{ cm}^{3} \text{ valeur approchée} \end{align*} \]

C) Section d'une sphère par un plan

Propriété
Lorsqu'elle existe, la section d'une sphère par un plan est un cercle.

Détaillons plus largement cette propriété.
Considérons une sphère de centre \(A\) et de rayon \(r\). Soit \(\mathcal{P}\) le plan sectionnant la sphère. Soit \((AH)\) la droite perpendiculaire au plan \(\mathcal{P}\) passant par le centre de la sphère \(A\). La distance \(AH\) est appelée distance du centre \(A\) au plan \(\mathcal{P}\).

Cas 1 : \(AH=0\)
Le point \(H\) est confondu avec le point \(A\).
La section de la sphère avec le plan \(\mathcal{P}\) est un grand cercle de la sphère ; il partage donc la sphère en deux hémisphères.

Cas 2 : \(0<AH<r\)
La section de la sphère avec le plan \(\mathcal{P}\) est un cercle de centre \(H\). D'autre part, le triangle \(AHC\) est rectangle en \(H\).

Cas 3 : \(AH=r\)
Le cercle est réduit en un point : le point \(H\). On dit que le plan  \(\mathcal{P}\) est tangent à la sphère au point \(H\).

Cas 4 : \(AH \geq r\)
Le plan  \(\mathcal{P}\) n'intercepte pas la sphère.



II) Parallélépipède rectangle (Pavé droit)

A) Définition (rappels)

Définition
Un parallélépipède rectangle (ou pavé droit) est un polyèdre régulier dont toutes ses faces, au nombre de six, sont des rectangles.
Il est défini par longueur \(L\), sa largeur \(l\) et sa hauteur \(h\).
Un pavé droit possède 8 sommets et 12 arêtes.

B) Aire et volume (rappels)

Propriétés
L'aire des faces d'un pavé droit est égale à :
\[ \mathcal{A}=2(Ll+Lh+lh) \] Le volume d'un pavé droit est égal à : \[ V=L \times l \times h \]

C) Section d'un pavé droit par un plan

Propriété
La section d'un pavé droit par un plan est un rectangle.

Illustration :
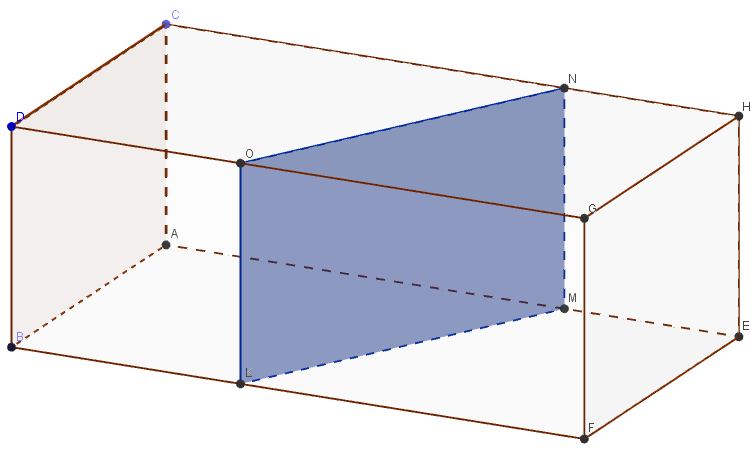
L'intersection entre le plan \(\mathcal{P}\) et le pavé droit \(ABCDEFGH\) est le rectangle \(LMNO\).



III) Cube

A) Définition (rappels)

Définition
Un cube est un polyèdre régulier dont toutes ses faces, au nombre de six, sont des carrés.
Un cube possède 8 sommets et 12 arêtes.

B) Aire et volume (rappels)

Propriétés
L'aire des faces d'un cube dont chaque arête mesure \(c\) est égal à : \[ \mathcal{A}=6c^{2} \] Le volume d'un cube dont chaque arête mesure \(c\) est : \[ V=c^{3} \]

C) Section d'un cube par un plan

Propriété
La section d'un cube par un plan parallèle à une de ses faces est un carré.

Illustration :
L'intersection entre le plan \(\mathcal{P}\) parallèle à la face \(CDHG\) et le cube \(ABCDEFGH\) est le carré \(MNKL\). 


Propriété
La section d'un cube par un plan parallèle à une de ses arêtes est un rectangle.

Illustration :
L'intersection entre le plan \(\mathcal{P}\) parallèle à l'arête \([BF]\) et le cube \(ABCDEFGH\) est le rectangle \(LMNO\).



IV) Cylindre

A) Définition (rappels)

Définition
Un cylindre de révolution est un solide constitué de deux bases circulaires parallèles et d'une surface latérale. Il se définit par le rayon de ses cercles \(r\) et par sa hauteur \(h\).

B) Aire et volume (rappels)

Propriétés
L'aire des faces d'un cylindre est égale à :
\[ \mathcal{A}=2\pi r(r+h) \] Le volume d'un cylindre est égal à : \[ V=\pi r^{2}h \]


C) Section d'un cylindre par un plan

Propriété
La section d'un cylindre par un plan parallèle à sa base est un disque de même rayon que le cercle de base.

Illustration :
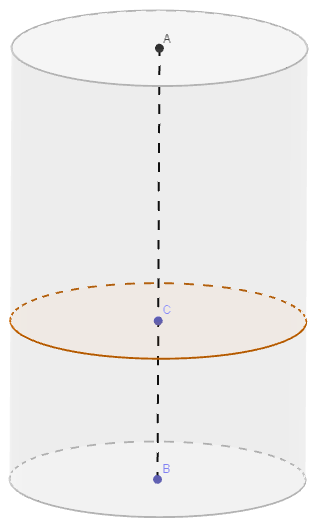
L'intersection entre le plan \(\mathcal{P}\) parallèle à la base et le cylindre est le cercle de centre \(C\) de même rayon que celui de base. 
cylindre

Propriété
La section d'un cylindre par un plan parallèle à l'axe est un rectangle.

Illustration :
L'intersection entre le plan \(\mathcal{P}\) parallèle à l'axe \([AB]\) et le cylindre est le rectangle \(DEJF\).
 


V) Cône

A) Définition (rappels)

Définition
Un cône de révolution est un solide constitué d'une base circulaire et d'une surface latérale possédant un unique sommet. Il se définit par le rayon de son cercle \(r\) et par sa hauteur \(h\).

B) Volume (rappels)

Propriétés
Le volume d'un cône est égal à : \[ V=\frac{\pi r^{2} h}{3} \]


C) Section d'un cône par un plan

Propriété
La section d'un cône de révolution par un plan parallèle à sa base est un disque de rayon inférieur au cercle de base.

Illustration :
L'intersection entre le plan \(\mathcal{P}\) parallèle à la base et le cône est le cercle de centre \(C\) de rayon inférieur à celui de la base (cercle de centre \(A\)). 


Propriétés
Le cône qui a pour base le cercle de centre \(C\) est une réduction du cône qui a pour base le cercle de centre \(A\). Le coefficient de réduction noté \(k\) est égal à :
\[ k=\frac{BC}{AB} \] En utilisant le théorème de Thalès, on peut déduire la relation existant entre le rayon du cercle de centre \(A\) (noté \(r\)) et celui de centre \(C\) (noté \(r'\)) : \[ r'=k \times r \] En particulier, lorsqu'on multiplie les dimensions du cône par \(k\), on multiplie son volume par \(k^{3}\).


VI) Pyramide

A) Définition (rappels)

Définition
Une pyramide est un solide constitué d'une base polygonale comportant au moins 3 côtés et de faces latérales triangulaires se rejoignant en un unique sommet. On appelle hauteur \(h\) le segment issu du sommet de la pyramide et perpendiculaire à sa base. Un tétraèdre est une pyramide dont la base est triangulaire.

B) Volume (rappels)

Propriétés
Le volume d'une pyramide est égal à :
\[ V=\frac{A_{\text{base}}\times h}{3} \]


C) Section d'une pyramide par un plan

Propriété
La section d'une pyramide par un plan parallèle à sa base est une réduction du polygone de base.

Illustration :
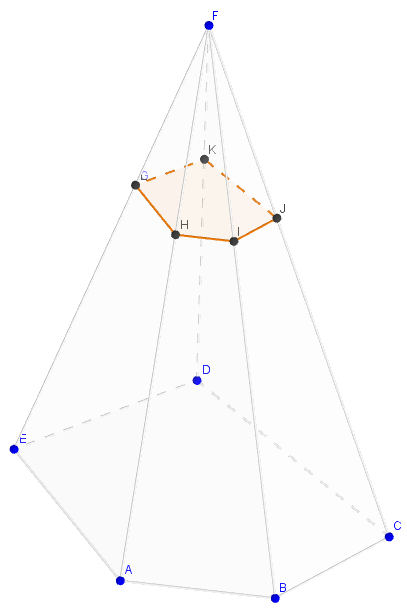
L'intersection entre le plan \(\mathcal{P}\) parallèle à la base \(ABCDE\) et la pyramide \(FABCDE\) est le polygone \(GHIJK\), qui est une réduction du polygone \(ABCDE\).



Propriétés
La pyramide \(FGHIJK\) est une réduction de la pyramide \(FABCDE\). Le coefficient de réduction noté \(k\) est égal à :
\[ k=\frac{FH}{FA}=\frac{FI}{FB}=\frac{FJ}{FC}=\ldots \] En utilisant le théorème de Thalès, on peut déduire la relation existant entre les dimensions de la base ABCDE et celle de la base GHIJK avec par exemple : \[ HI=k \times AB \] En particulier, lorsqu'on multiplie les dimensions de la pyramide par \(k\), on multiplie son volume par \(k^{3}\).

Cours sur la géométrie dans l'espace et les volumes pour la troisième (3ème)
© Planète Maths