AMERIQUE DU NORD JUIN 2016
Sujet du brevet

Exercice 1 (6 points)

Indiquer si les affirmations suivantes sont vraies ou fausses. Justifier vos réponses.
Affirmation 1 : La solution de l’équation \(5x+4=2x+17\) est un nombre entier.
Affirmation 2 : Le triangle CDE est rectangle en C.

Affirmation 3 : Manu affirme que, sur ces étiquettes, le pourcentage de réduction sur la montre est supérieur à celui pratiqué sur la paire de lunettes.

Exercice 2 (4 points)

1) Guilhem, en week-end dans une station de ski, se trouve tout en haut de la station. Il a en face de lui, deux pistes noires, deux pistes rouges et une piste bleue qui arrivent toutes à un restaurant d’altitude. Bon skieur, il emprunte une piste au hasard.

a) Quelle est la probabilité que la piste empruntée soit une piste rouge ?
b) À partir du restaurant, sept autres pistes mènent au bas de la station : trois pistes noires, une piste rouge, une piste bleue et deux pistes vertes.
Quelle est la probabilité qu’il emprunte alors une piste bleue ?

2) Guilhem effectue une nouvelle descente depuis le haut de la station jusqu’en bas dans les mêmes conditions que précédemment.
Quelle est la probabilité qu’il enchaîne cette fois-ci deux pistes noires ?

Exercice 3 (5 points)

Une station de ski a relevé le nombre de forfaits « journée » vendus lors de la saison écoulée (de décembre à avril).
Les résultats sont donnés ci-dessous dans la feuille de calcul d’un tableur.

a) Quel est le mois durant lequel la station a vendu le plus de forfaits « journée » ?
b) Ninon dit que la station vend plus du tiers des forfaits durant le mois de février. A-t-elle raison? Justifier.

2) Quelle formule doit-on saisir dans la cellule G2 pour obtenir le total des forfaits « journée » vendus durant la saison considérée ?
3) Calculer le nombre moyen de forfaits « journée » vendus par la station en un mois. On arrondira le résultat à l’unité.

Exercice 4 (4 points)

Sur un télésiège de la station de ski, on peut lire les informations suivantes :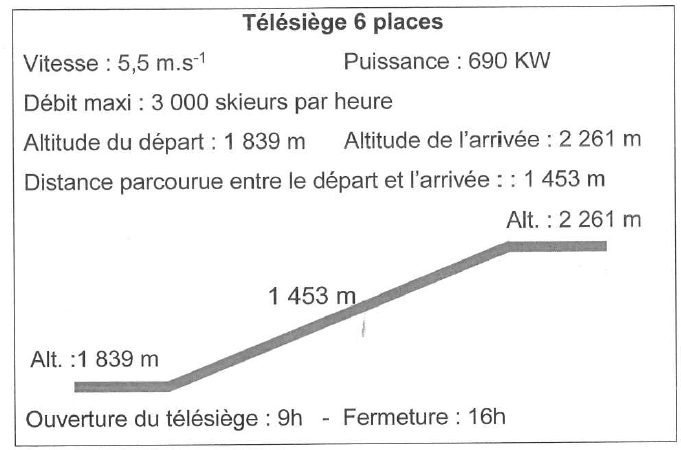

1) Une journée de vacances d’hiver, ce télésiège fonctionne avec son débit maximum pendant toute sa durée d’ouverture. Combien de skieurs peuvent prendre ce télésiège ?
2) Calculer la durée du trajet d’un skieur qui prend ce télésiège.
On arrondira le résultat à la seconde, puis on l’exprimera en minutes et secondes.
3) Calculer l’angle formé avec l’horizontale par le câble de ce télésiège. On arrondira le résultat au degré.

Exercice 5 (5 points)

Une station de ski propose deux tarifs de forfaits :

- Tarif 1 : le forfait « journée » à 40,50€.
- Tarif 2 : Achat d’une carte club SKI sur Internet pour 31€ et donnant droit au forfait « journée » à 32€.

1) Déterminer par le calcul :

a) Le tarif le plus intéressant pour Elliot qui compte skier deux journées.
b) Le nombre de journées de ski à partir duquel le tarif 2 est plus intéressant.

2) Utiliser le graphique ci-dessous qui donne les prix en euros des forfaits en fonction du nombre de jours skiés pour les deux tarifs.

Déterminer par lecture graphique :

a) Le tarif pour lequel le prix payé est proportionnel au nombre de jours skiés. On justifiera la réponse.
b) Une estimation de la différence de prix entre les deux tarifs pour 6 jours de ski.
c) Le nombre maximum de jours de ski que peut faire Elliot avec un budget de 275€.

Exercice 6 (7 points)

Sur l’altiport (aérodrome d’altitude) de la station de ski se trouve une manche à air qui permet de vérifier la direction et la puissance du vent.
Cette manche à air à la forme d’un tronc de cône de révolution obtenu à partir d’un cône auquel on enlève la partie supérieure, après section par un plan parallèle à la base.

On donne : AB = 60 cm, A′B′ = 30 cm, BB′ = 240 cm.
O est le centre du disque de la base du grand cône de sommet S.
O′ milieu de [OS], est le centre de la section de ce cône par un plan parallèle à la base.
B′ appartient à la génératrice [SB] et A′ appartient à la génératrice [SA].

1) Démontrer que la longueur SB est égale à 480 cm.
2) Calculer la longueur SO. On arrondira le résultat au centimètre.
3) Calculer le volume d’air qui se trouve dans la manche à air.
On arrondira au centimètre cube.
On rappelle les formules du volume d’un cône et l’aire d’un disque de rayon R :
\[ \begin{align*} &V_{\text{cône}}=\frac{1}{3}\times\text{ aire de la base}\times\text{ hauteur}\\ & A_{\text{disque}}=\pi \times R^{2} \end{align*} \]

Exercice 7 (5 points)

Un couple et leurs deux enfants Thomas et Anaïs préparent leur séjour au ski du 20 au 27 février.
Il réservent un studio pour 4 personnes pour la semaine.
Pendant 6 jours, Anaïs et ses parents font du ski et Thomas du snowboard. Ils doivent tous louer leur matériel.
Ils prévoient une dépense de 500€ pour la nourriture et les sorties de la semaine.

	06/02 - 13/02	13/02 - 20/02	20/02 - 27/02	27/02 - 05/03
Studio 4 personnes 29 m²	870€	1020€	1020€	1020€
T2 6 personnes 36 m²	1050€	1250€	1250€	1250€
T3 8 personnes 53 m²	1300€	1550€	1550€	1550€

Location de matériel de ski

Adulte : skis, casque, chaussures : 17€ par jour
Enfant : skis, casque, chaussures : 10€ par jour
Enfant : snowboard, casque, chaussures : 19€ par jour

Formule 1

1 adulte 187,50 € pour 6 jours
1 enfant 162,50 € pour 6 jours

Formule 2

Achat d’une Carte Famille 120€

Puis

1 forfait adulte 25€ par jour
1 forfait enfant 20€ par jour

1) Déterminer pour cette famille, la formule la plus intéressante pour l’achat des forfaits pour six jours.
2) Déterminer alors le budget total à prévoir pour leur séjour au ski.

AMERIQUE DU NORD JUIN 2016 Sujet du brevet